
【算数オリジナル問題】ジグザグ道の進み方の場合の数
こちらのオリジナル問題の解答編です。
【問題 再び】点Pの右側旅

完全オリジナル問題で「栄東中でも似たようなテーマを扱っている」などと書いたのですが、なんと本当に栄東中で同じ形を扱う入試問題があったようです→「どう解く?中学受験算数」様の記事。(自分では確認できていません。)ただ、私の問題の方が捻くれています。解説します。
【解説】ズバリ、フィボナッチ。
問題で言う「右側」というのは「真右か右上か右下」を意味しており、どの頂点からも2通りに分岐します。「道の進み方」の問題で定石の通り、各交点まで進む場合の数を足し算で次々に求めていってみますと、作業の中で「一つ前と二つ前の和が次の数になる」つまり「フィボナッチ数列が登場する」ことに気づけます。異常に増え方が大きいことからも勘づけるかも知れません。

フィボナッチ数列の問題といえば、「フィボナッチ数列の規則性を見抜かせて、10番目くらいを答えさせる」というのがお決まりの展開ですが…この問題は異様ですね。
【解説1】プ=ハン・パププーパ

図のように、パとプを基準にして右側の通りを書くと、点ピまで移動するには「パププ」通りあると分かります。よって、プ=(パププ-パ)÷2=(610-144)÷2=233通り。
※補足:図の左端の点、つまりパ+□=プとなる□を考えたくなることと思いますが、フィボナッチ数列は、途中で切っても「2つの連続する項」が分かっていればその後は足し算で表せますので、わざわざパとプの関係まで追求しなくてよいです。
【解説2】三三五五に珊瑚あり
問1を横に広げて強そうに見せているだけで、同じ考え方で解けます。大きい数をどうにか分解したいと考えてもらいたいですね。
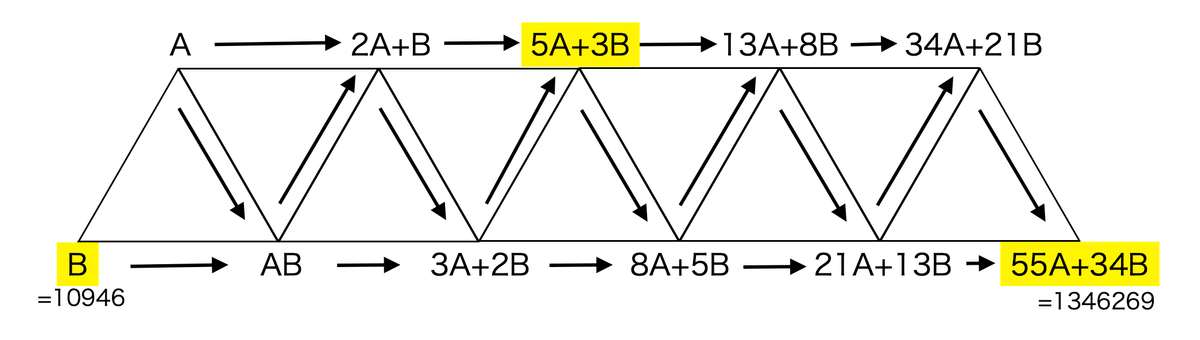
図のように、最初の2項をA、Bとすると、右側は次々とAとBの倍数の和で表されます(また、AとBにかける数もフィボナッチ数になっているのですね)。黄色が問題で示されている3点です。Aを求めるには10946×34を計算してもよいのですが、ここは{(55A+34B)‐B}÷11だけで簡単に5A+3Bに到着できます。(1346269‐10946)÷11=121393通り。消去算の逆算みたいな感じですね。面白い。
※補足:例えば初めの2項を一歩手前にずらしたとしても、89A+55Bを利用して8A+5Bを求めることになり、同じ工夫が使えます。また他の項同士もかなり近しい関係があるようです。
【EXTRA発展問題】
最初にフィボナッチ数列を道順で表現できそうだと思いついてから、色々な歪な形を経て正三角形に辿り着いたのですが、まさに「車輪の再発明」だったようです。ただ、問2ほどの活用は依然見たことがなく、面白いと思います。
さて発展問題。
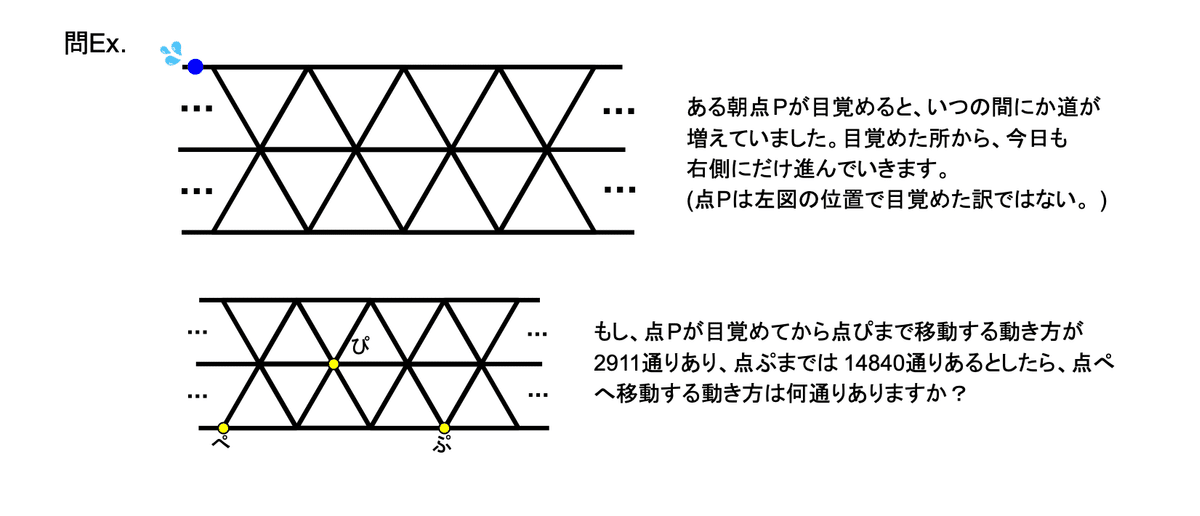
解答は285通り。記事をシェアしてくださると、解説もご覧になれます。
2023年12月8日
【↓解説Ex.↓】
ここから先は
おいしいコーヒーが飲めると集中力も想像力も高まります。 よろしければコーヒーサポートをお願いいたします😌☕
