少し専門的な流体力学の話

流体力学とは、文字通り力学的な視点から流体の運動を扱う学問です。

その中でも特に「加えられた力」と「それによって生じる変形の速さ(流速)」との関係が考察の対象となります。

流体(空気や水)が豊富な地球に居る以上、切っても切り離せない学問といえ次の土台となっています。
船舶工学、航空工学、宇宙工学、化学工学
水理学、河川工学、海岸工学、応用力学
環境工学、建築環境工学、流体素子

流体力学はキーワードが多く舌足らず感は否めませんが、これだけはと思った内容を出来る限り選び開設しました。
(もしくは続編を書くと思います)

最後の項目では、流体力学そのものの意義について説明しています。ご興味あれば是非ご覧ください。

流体とは

流体とは液体と気体のことです。
堅い表現で表すと「静止状態においてせん断応力が発生しない連続体の総称」です。

(せん断応力とは、物体内部のとある面で、滑るように切断的な破壊を起こす力のことです)

流体の種類

流体には「粘性流動」と「塑性流動」があります。粘性流動とは外力が働くと変形が直ちに生じる流体のことです。

一方、塑性流動とは、ある限度以上の力を加えると変形し、それ以下の力では単に材料がひずむだけで形態を保つ流体のことです。


後者の塑性流動は、さらに変形速度から分類できます。ある一定の変形を生じさせるのに必要な力が、変形速度に比例する場合をニュートン流動、比例しない場合を非ニュートン流動と言います。

圧縮性について

流体は圧力の変化に伴ない体積が変化します。この性質を圧縮性と呼びます。水で満たされた注射器と、空気で満たされた注射器をイメージすると早いです。

液体は大きな圧力を加えてもほとんど変化しません。そのため非圧縮性流体とみなすことができます。一方で、気体は大きな圧力を加えると縮みやすく、圧縮性流体とみなすことができます。


ただし気体には例外があり、気体の運動速度が音波の伝播速度よりはるかに小さいときは圧縮性を無視できます。

突然、音の伝播を比較対象として持ち出したため混乱しますが、それは音が伝わる物理的メカニズムを考えれば解ります。音は気体が隣の分子に衝突して気体の疎密の状況を次々と伝えていく現象です。つまり音の伝播は、気体の運動による副次的現象です。

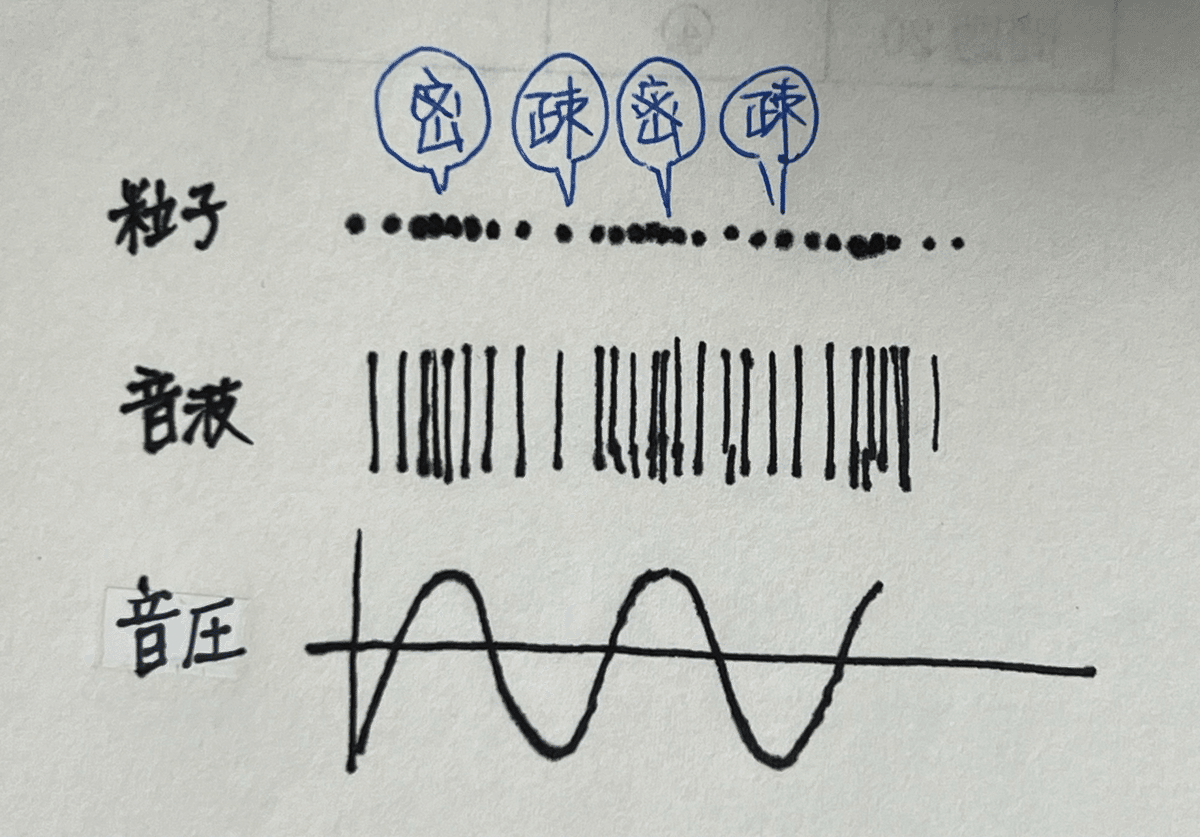
粘性について

粘性とは流動を妨げようとする性質のことです。水や空気は粘性が小さくサラサラし、油は粘性が大きくドロドロしています。

見方を変えると、流体全体の速度変化をなだらかにする作用でもあります。
(流体速度の分布が一様でない場合、速度差をならして一様にしようとする性質)

例えば、粘性によって流体は固体表面に粘着するし、その固体表面が動いていた場合は、固体との距離に応じて流体の動きもなだらかに減少していきます。

流体の速度分布(上側移動、下側静止)

実際の流体は多かれ少なかれ粘性を有する粘性流体ですが、固体面から遥か離れた場所における運動を論ずる場合は、一般に粘性を無視できます。

このように粘性のない理想的な流体は「理想流体」または「完全流体」と呼びます。

境界層について

粘性が働く場合、物体表面では流速0となります。一方、物体から非常に離れたところでは粘性は無視できます。

ではこの粘性の有効範囲はどこまででしょうか。

その定義が境界層です。一般に物体表面から、速度が主流速度の99%に達するまでの領域を境界層と呼びます。別の言い方をすると、流体中で静止物体を動かすとき、物体に引きずられて動かされる物体表面付近の流体の層です。

この境界層の厚みは粘性が大きいほど厚くなります。

また、この境界層は層流状態の「層流境界層」と乱流状態の「乱流境界層」に大別されますが、キリがありませんのでこの辺で打ち切ります。層流や乱流など、流体の乱れ具合についてはまたそのうち続編で触れようかと思います。

流体の支配方程式

力学と学問体系は同じため次式がベースとなっています。
ma=F(質量×加速度 =力)

ただし流体力学では、流れを記述するとき、流れの中の、ある特定の部分の流体に着目します。流れ全体を、無限に小さい1つ1つの流体粒子から考察するわけではありません。


また、流れの式を立てるにあたり、ベースとする座標系にも違いがあります。空間的に固定された座標を使うのか、あるいは粒子と共に動く座標系を使うのか決める必要があります。

前者の記述法をオイラー記述、後者をラグランジュ記述と言います。


オイラー記述では空間内に固定された座標に着目して、その点における流速を時間の関数として扱います。

一方、ラグランジュ記述では運動する個々の流体粒子に着目し、それが時間経過に従い空間内にどのような軌 跡を描くかを考えます。流体粒子の間に働く力に依存する瞬間的な速度場を示すことが難しく、理論的な扱いが難解になります。

流体力学の意義

流体は本来、膨大な質点から成り立っています。(アボガドロ数6.02 × 10の23乗 ) 

そのため流体の運動を記述するには膨大な方程式が必要です。さらに、忠実な運動を再現するとなると初期条件や境界条件も必要となり、現実的ではない情報量となります。

一方で例えば私達が普段台風について話すとき気体1粒子ごとの動きについては言及していません。時間的にも空間的にも、ある程度の範囲内で平均化したマクロ的な速度を考えています。

実用的にもこちらの考えが重要となります(場合に寄りますが)。

このとき役に立つ方程式は個々の質点を扱うニュートンの運動方程式ではなく、それをある程度平均化した方程式になります。

これが流体力学の役目です。この平均化した方程式によって流体のマクロな運動を記述することができます。