「３」のマジック

　言いたいことは「1 や 2 だけでは一般化できないが、3 までやれば一般化できる」、だから「２でやめるな。３までやれ。４はいらない」。 人間関係、ドミノ倒し、ババ抜き、足し算、掛け算を取り上げて例証します。

三角関係がコミュニケーションの基本形

　１人ではコミュニケーションがとれない。２人ならコミュニケーションとれるが、発展しない（男女関係であれば、ラブラブかケンカかのどちらかだろう）。さて、３人いたらどうなるかというと、これがなかなか微妙なのである。この場合、「３人のうちの２人が仲良くなって１人が取り残される」などいろんなバリエーションがあって、ちょっとしたことで３人の距離感がコロコロ変わったりする。（男女の場合、これを三角関係という）
　でも、３人でコミュニケーションがとれれば、同じやり方で４人の場合にも、５人の場合にも対応できる。そして、100人の集団であっても、３人のコミュニケーションのスタイルが応用できるのである。すなわち、「n人のコミュニケーション」において、n＝1 や n＝2 だけでは一般化できないが、n＝3 までやれば一般化できるのである。

　小学校の算数で他の例を考えよう。２つの数の足し算をする場合、繰り上がるときに十の位に1を足す（図１）が、これだけでは一般化できない。ところで、３つの数の足そうとすると、繰り上がるときに足す数は1だけでなく、2の可能性も出てくる（図２）。そして、ここまでやれば、４つの数の足し算、５つの数の足し算にも対応できるようになるのである。

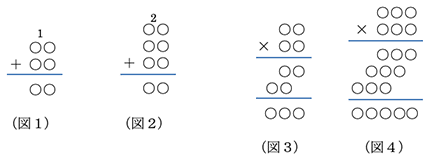
　あるいは、掛け算をするときに、数字を１つずつ左にずらしながら書く。２ケタの掛け算であれば、数字をずらして書くのは１回だけ（図３）だが、これだけが出来ても本当に掛け算のやり方が理解できているかどうか怪しい。ところで、３ケタの掛け算をするときは、数字をずらして書くのが２回（図４）になって、ここまでやれば「４ケタの掛け算でも、５ケタの掛け算でも同じようにやればいいんだな」とわかるのである。

　高校数学でも例をあげてみると、２次元での処理が大半で、３次元の扱いが非常に少ない。関数はほとんどが y = f (x) の形で、y を求めるためのパラメータは x だけ。グラフ化すると平面に描ける。数学Ⅲではかなりマニアックで難しい計算も入ってくるが、でもやっぱりほとんどが y = f (x) 型だ。けれどもこれでは、パラメータが増えたときにまるで対応できないのである。
　女性に聞いてみよ。「あなたの理想の男性は？ 結婚するなら、どんな男性がいい？」と。きっと答えるだろう。「やさしくて、ハンサムで、経済力のある人がいいわぁ」とかなんとか。そう、世の中、１つのパラメータで決まるわけがないのである。
　ところで、関数 z = f (x , y) を学習すれば、パラメータが３つになっても４つになっても対応できる。 関数 z = f (x , y) をグラフ化すると３次元になる。３次元がわかれば、４次元も５次元もわかる。

　ここで、今日の結論。「２でやめるな。３までやれ。４はいらん。」
　カップルでラブラブするのは簡単だが、発展性がない。三角関係は面倒だが、それは四角関係、五角関係へと発展して、やがて円関係になってまるく収まるのである。
　小学生は３つの数の足し算、３ケタ同士の掛け算を練習せよ。そうすれば、どんな足し算でも掛け算でもできるようになる。
　高校生は関数 z = f (x , y) と空間ベクトルを勉強せよ。そうすれば、パラメータが増えても対応できるし、n 次元空間でもイメージがつかめるようになる。
　３までやれば、一般化できるのである。

ドミノ倒しの原理

　ドミノ倒しというからには、パイは少なくとも３つ必要だ。パイ１つを倒しても、ドミノ倒しとは言わないだろう。１つのパイがバタンと倒れた、それだけの話である。
　パイ２つでも、やっぱりドミノ倒しとは言えない。実際、２つのパイを倒すのは簡単だ。パイの大きさ・位置が雑であっても大抵倒れる。
　ところが、パイが３つになると途端に難しくなる。パイの大きさをそろえ、等間隔に並べることが必要になる。そして、ここが大事なポイントだが、パイ３つでうまくいけば、パイの数を増やしてもうまくいく。
　鍵は真ん中のパイにある。真ん中のパイは、前のパイに押されて自らが倒れながら次のパイを倒す。ドミノ倒しをリレーするのは、このパイである。ところがパイ２つでは、これにあたるパイが無い。

　ところで、この仕組みを数学の証明に使うこともできる。その証明法を「数学的帰納法」と呼ぶ人もいるが、「ドミノ論法」と呼ぶ方がふさわしい。それがどんな証明法かと言うと、「ドミノ倒しの原理」そのまんまである。ドミノ倒しが成功するためには、次の２つの条件が必要である。

　　○　あるドミノが倒れると、その次のドミノも倒れる。
　　　　（n＝kで成り立つと仮定すると、n＝k+1でも成り立つ）
　　○　最初のドミノは自分で倒す。（n＝1で成り立つ）

　どちらか一方だけではドミノ倒しは成功しないが、この両方が成り立てばすべてのドミノがきれいに倒れる。他の条件は要らない。つまり、この２つの条件が、ドミノ倒しが成功する（すべての自然数で成り立つ）ための必要にしてかつ十分な条件なのである。

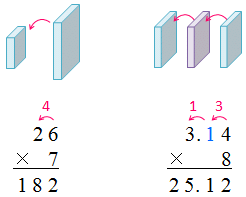
　話は突然変わって、掛け算の話。繰り上がりを見てみよう。２桁の掛け算の場合、１の位の数は繰り上がりを送るだけで、十の位の数は繰り上がりを受け取るだけ。確かに繰り上がりは発生しているが、これでは一般化できないのである。
　では、３桁の掛け算ではどうかというと、十の位を見てみよう。十の位の数は、一の位から繰り上がりを受け取りながら、百の位に繰り上がりを送る。このように、３桁の掛け算の場合は、十の位が繰り上がりをリレーする。ドミノ倒しと同じ原理である。
　このリレーは、４桁の掛け算でも５桁の掛け算でも発生する。ところが、２桁の掛け算ではこのリレーが発生しない。だから、２桁の掛け算ができても、３桁の掛け算ができるとは限らないのである。でも、３桁の掛け算ができれば、４桁の掛け算も５桁の掛け算もできるようになる。手順は３桁の掛け算の場合と同じだからである。

ババ抜きは３人以上でやれ

　話はまたまた変わって、今度はババ抜き。さて、２人でババ抜きをすると、どうなるか？　試してみよう。まずカードを配って、同じ数字のカードを捨てる。この時点でどちらがババを持っているかは、お互いに分かる。自分がババを持っていれば相手は持っていないのだし、自分が持っていなければ相手が持っているはずだからである。ババ以外の数字も全部分かる。相手は自分と同じ数字のカードを持っているからである。さて、次に相手のカードを１枚引く。このときババを引いたかどうかも、お互いに分かる。そしてババを引かなかった場合は、必ず同じ数字のペアが出来て、捨てることになる。すなわち、お互いが持っているカードも引いたカードも、常にお互いに周知しているのである。こうしてきっと、つまらないババ抜きになるだろう。

　でも、３人でババ抜きをすると、途端に面白くなるのである。まず自分がババを持っていない場合、誰がババを持っているか分からない。自分がババを持っている場合でも、しらばっくれていれば相手に知られることもない。また、誰かがカードを引いたとき、ババが移動したのか移動しなかったのかも分からない。自分がカードを引いたとき、それがペアになって捨てられるのか、捨てられないのかも分からない。こうして、３人いれば、スリル満点のババ抜きが実現するのである。
　この面白さは、４人でババ抜きする場合も、５人でババ抜きする場合も維持される。ところで、僕がなぜこんなことを言うかというと、「２でやめるな、３までやれ」を訴えたいからである。「２は発展しないが、３は一般化できる」ことを実証したいからである。そして小学生には「面倒がらずに、３桁どうしの掛け算の練習をしろ」と、高校生には「難しくても、空間ベクトルをしっかり勉強しろ」と言いたいからである。
　最後に、１人でババ抜きすることを考えてみよう。まずカードを配るが、結局は全部自分のところに来る。次に同じ数字のペアを捨てていく。ペアを作っては捨て、作っては捨てるうちにカードが減っていって、最後にババが残って、自分の負け。やっぱりババ抜きは３人以上でやった方がいい。

　結局のところ何が言いたいかというと、
　　○　n＝1 や n＝2 だけでは一般化できないが、
　　　　n＝3 までやれば一般化できる。
だから、
　　○　２でやめるな。３までやれ。４はいらない。
そういうこと。

◇　　　　　　◇　　　　　　◇

〜 １と２と３、そして無限 〜
▷ １の不思議　　　　　　
▷ ２のｎ乗のザックリ計算
▷ 「３」のマジック　　　
▷ 無限のいかがわしさ　　

〜 私の数学教育論 〜
▷ 結論を言わない証明問題　＋　解答編
▷ 数学屋が売れる時代になってきた　　
▷ 「３」のマジック