見出し画像

後日談 : 凸クラスタリング

Azalea

あらすじ

前回は自身の勉強のための凸クラスタリングについて記事にしました．記事の内容については，なるべく分かりやすいように書いたため，ぜひご参照ください．

さて，凸クラスタリングの原理や内容については詳しく記述いたしましたが，プログラムについて補足したほうがいい箇所があるので，後日談として記事にします．

イキサツ

今回は凸クラスタリングのプログラムの補足をしていきます．具体的には，重要度πの更新式が説明対象になります．ここは割と頭を使って，きれいに書きました(えらい!) . このプログラムの組み方は，コーディングするうえ(特にPython)で重要になってきます．何が重要かって? 可読性？いやいや，機械学習においてはfor文を使わないことが重要です．

プログラム

import sys
import os
import numpy as np
import pdb
import time
import pandas as pd
   

x = np.genfromtxt('data.csv',delimiter=',')

i = 0
s = 0.05
d = x[0].size
n = x[:,0].size
times = 1000

pi = np.ones(n) / n
estPi = np.ones(n) / n
xmx = []
f = []


# ベクトルのノルムの2乗を計算
x_norm_squared = np.sum(x ** 2, axis=1)

# ベクトル同士の積の内積を計算
dot_product = x.dot(x.T)

# ユークリッド距離を算出
distance_matrix = np.sqrt(np.abs(x_norm_squared[:, np.newaxis] + x_norm_squared - 2 * dot_product))

f = (2*np.pi*s*s)**(-d/2) * np.exp(-1/(2*s*s)*distance_matrix*distance_matrix)

while(i<times):
    pi = np.sum((pi * f).T / np.dot(pi,f), axis=1) / n
    i += 1

説明対象のコードは下から2番目の

pi = np.sum((pi * f).T / np.dot(pi,f), axis=1) / n

になります．1文で完結しておりきれいですね．重要度の更新は下記で示されます．

重要度πの更新式

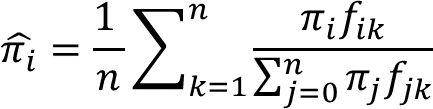
通常，頭を使わずにこれを組もうとすると，三重ループを以下のように組むことになります．

    piPre = pi.copy()
    for i in np.arange(n):
        sumBuf = 0
        for k in np.arange(n):
            piF = 0
            for j in np.arange(n):
                piF += piPre[j]*f[j,k]
            sumBuf += piPre[i]*f[i,k] / piF
        pi[i] = sumBuf / n

式をそのままコーディングしているので，分かりやすさはこちらのほうが上ですね．では，実行時間はどうでしょうか？
ちなみに，凸クラスタリングの記事内に記載してあるfor文を使わないプログラムの実行時間は約0.17秒になります．そこそこ，早いですね．色々なデータで試したりすることが可能です．
一方，こちらのプログラムの実行時間は13731秒かかりました．約4時間です!

遅い! 遅すぎる!

ちなみに，実験条件はCore i7-8700のメモリ16G，Spyder5.3.2，Python 3.9.12の64bitになります．多少，古いパソコンにはなりますが，それでも4時間は遅すぎます．for文を使わない方と比べると80770倍もの実行時間にもなります．

えらいこっちゃ! えらいこっちゃ!

さて，実行時間の大事さはご理解いただけたと思います．ただでさえ，学習で回数を必要とするのに，1回の学習で何回も繰り返し計算を行っていては，相当な時間がとられます．
また，会社など納期がある方に関してはこの限りではありません．とりあえず，動くものを期間内に作り上げることは大切です．一方，デバックするのに4時間待つのはいかがなものでしょうか？ それなら，2,3時間くらい頭をひねっても文句は言われなさそうですよね．

プログラムの説明

では，実際にプログラムの解説に移っていきたいと思います．
この更新式では行列計算を軸に書いております．

行列計算と聞いて頭が痛くなったあなた!

その反応自体は正しいのですが，機械学習系のプログラムには必須事項になりますので，その痛みに慣れていきましょう．
まずは，この式を行列っぽく変換していきます．注意点としては，完璧な行列変換は致しません．プログラム上で扱えるような形にするだけです．
この形の目的は総和(Σ)をなくすことにあります．
このため，行列っぽい形にして，行列演算っぽいことをしていきます．

行列の導入

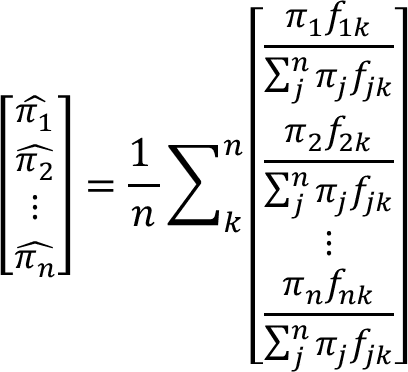
それっぽく書いてありますが，ほぼ更新式のままになります．左辺の重要度πに合わせて右辺が変更されているだけです．
あと，言い忘れていましたが，総和(Σ)などの計算は基本的に行列式に変換可能です．なので，更新式をみて「ここが行列っぽいなぁ」と考えることが大切になります．

大枠の展開

さて，話をもどします．まずは，総和(Σ)の展開をしていきましょう．

総和(Σ)の展開

ここまではいたって普通の式変換を行ってきました．ここからは，ちょっとクセの強い変換を行います．要素ごとや規則性の高い四則演算は行列の要素計算として演算可能になります．通常の行列計算であれば，内積・外積，要素同士の加減算が基本ですが，プログラムではこの計算の自由度が高くなります．例えば，行列の行部分だけ加算するといった具合です．
そこで，展開したものを次のように変換します．

演算を見込んだ行列化

この様に，先に演算を見込んで変形しておきます．この行方向の足し算はnp.sum(~~~, axis=1)がソースコードで対応しています．
また，分母でも同様のことが行えそうですね．

演算を見込んだベクトル化

このベクトル・行列として変換するというのは，中学生の頃の因数分解に似た感覚ですね．また，演算を見込んで変換するのは，ほぼパズルを解いているときと同じな気がします．ソースコードでではnp.sumの中の通常の割り算(/)ですね．
一応，ベクトル扱いなので分母のベクトルには転置(T)をつけています．なので，横ではなく縦だと思ってください．

分母の展開

さて，分母の総和(Σ)もとりたいので展開していくと，ベクトルと行列の内積っぽい計算が可能です．

内積っぽい演算

ここで，「っぽい」とつけているのは正確には内積ではないのでこれがついております．ちなみにこの演算はソースコードでnp.dot(pi,f)が担当しております．
これでほとんどが終了しましたね!
分子の展開もちゃっちゃと終わらせましょう!

分子の展開

外積っぽい演算

これで，分解+総和(Σ)の除去が終わりました．数式っぽくまとめると下記のとおりです．

行列展開のまとめ

総和(Σ)がなくなっており，各行列成分でまとまっているのが確認できます．実際のソースコードではこちら．

 pi = np.sum((pi * f).T / np.dot(pi,f), axis=1) / n

数式もソースコードと同じ感じがでてますね!
ね! 簡単でしょ!
鋭い方はお分かりかもしれませんが，このソースコードの構築は厳密な計算していません．「こうなったら展開できるから，この仕組み(計算)はあるかな？」といった，ツール探しをひたすら行っているだけです．そんなに難しいことをしているわけではありません．入力を出力に変換したいときの変換ツールの模索です．

小話

プログラムの実装は「頭で構築する時間が主，実装and実行は一瞬」というのが一番良いと私は思います．これは，同じソースコードを一回しか考えないのに対し，実行は何度もするためですね．
実装まで一瞬というのは大規模なもに対しては無理なのですが，上記のソースコードのような少ない行数で書けるものが好ましいと考えております．
また，今回は皆様にわかりやすくするため，「大枠展開→分母展開→分子展開→行列展開まとめ」とこのような順番で書いてます．一方，実際には全く逆の順番で頭の中でソースコードを構築します(私の場合)．
なので，実際の思考は

  1. 重要度πをベクトルとして一気に演算できればうれしいなぁ(目的)

  2. 分子分母を各行列から計算できたらいけそうだよね

  3. 行列っぽい計算はいけそうだなぁ．割り算もいけたらうれしいなぁ

  4. ベクトルと行列の割り算も大丈夫そうだし，あとは行方向に足し算して

  5. 完成!

こんな感じになります．これはあくまで私の思考のプロセスなので，他の方がどのように考えているかはわかりかねます．これは思考のプロセスの問題で，日常的なことが反映されていると思われます．現に，駅から目的地の行き方も私はこんな感じですね．駅を背中にした時の目的地の方角をある程度決めて，いったんそっちに進み，近くなったら微調整します．
皆様の思考のプロセスはどのような感じですか？ とても興味がありますね!

まとめ

今回は，以前書いた凸クラスタリングのプログラムについて，ちょっとした解説を書きました．この実行部分にはちょっと自信があったので，子供みたいに「みてみてー!すごでしょー!」したくなったので，ご容赦ください．大人になると褒められる回数がすくないので．
ここまで，読んでいただき誠にありがとうございます．
多少，時間をかけて書いておりますので，スキ・フォローやシェアしていただければとても嬉しいです．また，読者の皆様のお役に立てればより幸いです．


この記事が気に入ったらサポートをしてみませんか？