
機械学習の勉強 Part1 : 凸クラスタリング
イキサツ
これまで,研究の関係で機械学習について勉強しておりましたが,ノンパラメトリックに関する勉強を疎かにしておりました(理論難しすぎない?) .
というわけで,ノンパラを理解するために今回は凸クラスタリングについて勉強メモとして,残していきたいと思います.
概要
確率分布に基づいたクラスタリング手法のなかでも比較的に簡単な凸クラスタリングを扱っていきます.参考書はオーム社の「続・わかりやすいパターン認識―教師なし学習入門」です.
今回は数式や詳細を控えめにして概要や実装について書くため,詳しいことが知りたい方は本を買ってください(研究分野への貢献として).
また,拙い文章と間違いがある可能性があるのでご容赦下さい.
基礎知識
人工知能・機械学習分野における基礎知識を少々(スパイス風).
機械学習の分野には様々な学習の方法がありますが,大きく分けて3つあります.
教師あり学習・教師なし学習・強化学習 ※諸説あり
教師あり学習はデータとラベルが対応している状態から始めて,この2つの対応関係を表現するのが学習の目的になります.
例 : 性別による身長差,画像から動物を分類などなど
教師なし学習はデータしか持っていない状態で,このデータをどの様なグループに分けるか?この分類を表現することが学習の目的です.
強化学習はややこしいので省きます(許して).この学習だけ上記の2つと違うので,また別の機会に
クラスタリング
今回の凸クラスタリングを含めたクラスタリングは,教師なし学習に所属します.データの分布からクラスタリングでグループを形成し,人間が各グループにラベルを付与させることが目的となります.

クラスタリングはあくまでグループ分けだけになります.
その後の解釈は人間側で行うのが通常です.また,ここから少しややこしいのですが,このグループ分けにも種類があります.ざっくり言うと,
グループの数が分かっている or 分かっていない
分かっている場合はクラスタリングによって分類されたグループとデータとの相関など,関係性を解析する傾向にあります.これは,そもそもデータに対する傾向などの知識がある場合に多いです.
分かっていない場合は,いわゆる初見さんですね.初めてデータ見たよ!事前知識ないよ!とりあえず,人間がわかりやすいようにグループ化しよう!
こんなノリです.
各場合の代表手法ですが,グループ数が既知ならK-means,グループ数が未知なら凸クラスタリングと思っておいてください(DBSCANとかもあるかも).
正規分布
凸クラスタリングは,確率分布である正規分布に基づいてクラスタリングを行います.正規分布の形はこんな感じです.
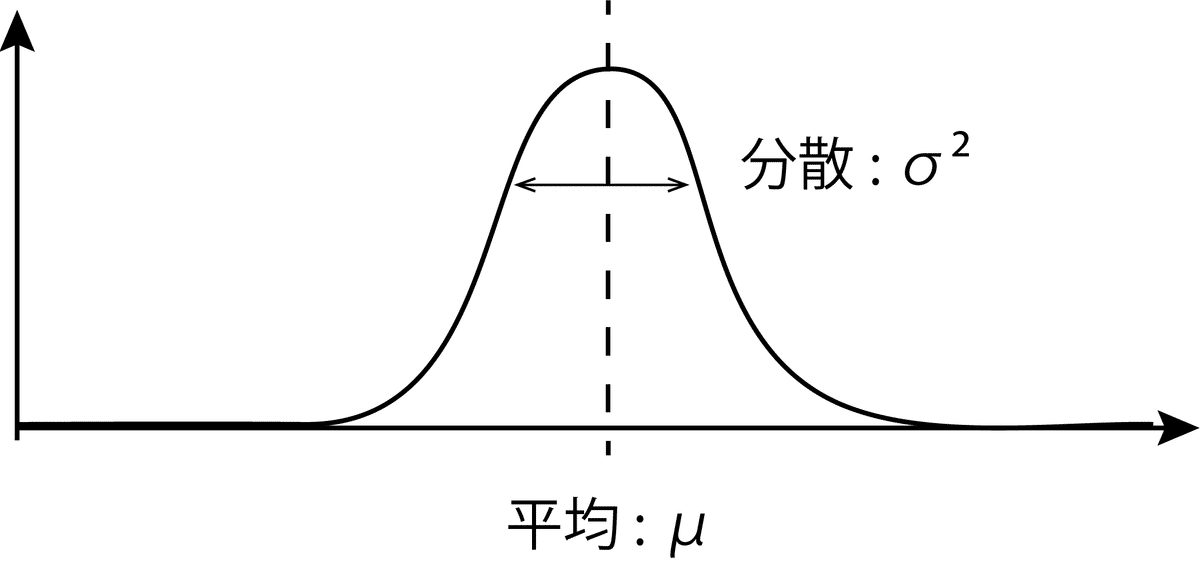
理解としては平均に近いと確率が上がる分布だと思ってください.
また,分散は横の広がりを示しています.大きければ大きいほど,横に広く縦に低い分布になります(σだけだと標準偏差 : 片側の広がりを示します).
確率分布を使ったクラスタリングは,これらのパラメータ(平均μ,分散σ2)を求めていきます(求めないやつもあります : ノンパラ…) .
凸クラスタリングでは各正規分布の算出値を求めることで,グループ分けを行います.
まずは,正規分布の式を記します.

ちょっとまって!いかないで!なるべく,わかりやすく説明するから!
まずは,出てきてない文字の定義ですね.xはd次元のデータです.
今回は扱いやすいので2次元とします.なので,例えばx = [1,2]みたいな感じです.2次元なのでd=2になりますね.
続いて,式に関してですがこれも思った以上に難しくありません.
expの外側(左側)ですが,これは調整用の値です.確率分布は1を超えてはいけません.でも,expの中身を使いたいけど1を超えてしまう!
こんな理由で,係数がついてます.極論,これは気にしなくていいです.
本題のexpの中身ですが,これも身構えないでください.|x-μ|の部分は平均とデータの距離を表しているだけです.この距離に対して,分布の広がりをあてはめて確率を算出してます.
わからなくても問題ないので,こういうもんなんだなっと思ってください.
計算できればokです(・∀・)
凸クラスタリング
前提条件
では,実際にどのようなプロセスでクラスタリングしていくかに移ります.
正規分布の平均値をどうやって決めるか?(分散はあらかじめ付与)
データはあるがグループの数が未知
現在の条件は以上になります.まずは,グループの数から決めていきましょう.そこで,偉い人は以下のような力業を思いつきます.
「グループの数がわからなければ,一旦すべての各データを各グループとみなそう!」
つまり,データ数 = グループ数 になり,1人のグループが完成しました.
は??
お気持ちお察しします.でも,この発想と真逆の発想(一旦,すべてのデータを1つのグループとしよう!)がよく出てきます.これくらいでキレてたら,体力が持ちません.冷静に行きましょう.
もう少し,詰めた話をしましょう.データの数だけ正規分布を作成し,ここから確率を算出いたします.この確率をもとに各正規分布の重要度を決めていきます.この重要度が高いものだけ,残せばグループ分けできそう!
といった発想です.ここで,重要度πを以下のように定義します.

正規分布がデータ数分だけ存在するので,重要度も同様にデータ数だけ存在します.また,複数の正規分布を組み合わせた分布を混合正規分布といい,そこでは重要度πではなく,混合度αと呼ばれます(おそらく,こっちのほうがメジャー).
確率の算出
分布の定義が決まったので,実際に確率を算出していきましょう.クラスタciの正規分布にデータxkを入力したときの値は以下の通りです.

さて,ここで問題なのは平均値μですね.こいつの決め方が問題となります.今回のクラスタリングで機械的に求めるパラメータはあくまで重要度πになります.なので,分散σと同様に平均値μも決め打ちしなくてはいけません.
どうすると思います??
正解は,データxで置き換えます!鋭い方はお察しだったと思います.
各グループに存在しているデータは1つしかないので,平均値もそのデータになるということです.ただし,データ1つだと分散が出ないので,今回の分散は0.1とか0.05とかの固定値にしてしまいます.
と,いうことで計算を書き直すと

となります.
確率算出では他の正規分布の値と比較して確率を算出するので,クラスタciにデータxkが所属する確率は下記になります.
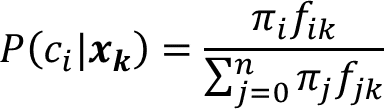
単純ですね!
分母が全部の正規分布の値と重要度の総和,分子が対象のクラスタの値でこれらの比率をとって確率としております.
コーヒーブレイク
次は重要度の更新ですが,複雑な式変形や理論は参考書を買って(ここ大事!) ,お読みください.ちなみに,私は参考書の著者の方を知りませんし,広告などでもございませんのであしからず.ただ,各業界,分野にお金を落とすことはそこを伸ばすことと同義なので,研究系に貢献していただければ幸いです.ちなみに,参考書を買っていただいて研究分野に貢献できるのかも知りません(基本的に適当で無責任です).
重要度の更新
さて,重要度πの更新ですがこれも数式や難しい理論を負わなければ簡単です.端的に,重要そうなやつは確率高いよね?こんな感じで進んでいきます.先ほどの確率計算を全データで行って,重要度πを更新します.

左辺のハットをかぶってる重要度πが更新後になります.これを何度も繰り返すことで,重要度πが更新され,データの中心がわかるといった仕組みですね.
「なんでこうなるんだ?」と思ったそこのあなた!
ぜひ,前章のコーヒーブレイクをお読みください.
プログラムと結果
もう終盤になります.今回実装したプログラムを下記に載せます.
import sys
import os
import numpy as np
import pdb
import time
import pandas as pd
x = np.genfromtxt('data.csv',delimiter=',')
i = 0
s = 0.05
d = x[0].size
n = x[:,0].size
times = 1000
pi = np.ones(n) / n
estPi = np.ones(n) / n
xmx = []
f = []
# ベクトルのノルムの2乗を計算
x_norm_squared = np.sum(x ** 2, axis=1)
# ベクトル同士の積の内積を計算
dot_product = x.dot(x.T)
# ユークリッド距離を算出
distance_matrix = np.sqrt(np.abs(x_norm_squared[:, np.newaxis] + x_norm_squared - 2 * dot_product))
f = (2*np.pi*s*s)**(-d/2) * np.exp(-1/(2*s*s)*distance_matrix*distance_matrix)
while(i<times):
pi = np.sum((pi * f).T / np.dot(pi,f), axis=1) / n
i += 1 こんなに長く解説?したのに,プログラムでは一瞬ですね.結果のgifも張っておきます.

データの中心が色づいてるのがわかると思います.あとは,重要度の値を閾値などで区切ってあげれば完成ですね!
また,今回は一番最初の重要度πは同じ確率(1/n)で与えております.分散も0.05です(この設定に苦労します).
まとめ
今回は自分の勉強ついでに,教師なし学習の1つである凸クラスタリングについて書きました.詳しいことは他の人の記事や参考書をお読み下さい.この記事は概要をつかむことに特化しております.多少,時間をかけて書いておりますので,スキボタンやシェアしていただければ幸いです.
また,読者の皆様のお役に立てればよりうれしいです.
備考
gifを生成するプログラムも書いておきます.また,更新式のプログラム(whileの所)が少し難解なので,別記事にて解説をさせていただきます.
皆様の勉強の手助けになれば幸いです.
import sys
import os
import numpy as np
import pdb
import time
import pandas as pd
import matplotlib.pyplot as plt
x = np.genfromtxt('data.csv',delimiter=',')
i = 0
s = 0.05
d = x[0].size
n = x[:,0].size
times = 1000
pi = np.ones(n) / n
estPi = np.ones(n) / n
xmx = []
f = []
# ベクトルのノルムの2乗を計算
x_norm_squared = np.sum(x ** 2, axis=1)
# ベクトル同士の積の内積を計算
dot_product = x.dot(x.T)
# ユークリッド距離を算出
distance_matrix = np.sqrt(np.abs(x_norm_squared[:, np.newaxis] + x_norm_squared - 2 * dot_product))
f = (2*np.pi*s*s)**(-d/2) * np.exp(-1/(2*s*s)*distance_matrix*distance_matrix)
fig, ax = plt.subplots()
# 散布図をプロットする
sc = ax.scatter(x[:,0], x[:,1], c=pi, cmap='cool', alpha=0.8,vmin = 0, vmax =0.5)
# カラーバーを追加する
cbar = plt.colorbar(sc)
cbar.ax.set_ylabel('Importance')
# アニメーションのフレームを設定する
colors = np.linspace(0, 1, times) # 色の範囲を0から1に設定する
def update(times):
global pi,f
pi = np.sum((pi * f).T / np.dot(pi,f), axis=1) / n
# 各フレームごとに散布図の色を変更する
sc.set_array(pi)
ax.set_title(f'Frame {times}')
return sc,
# アニメーションを作成する
from matplotlib.animation import FuncAnimation
anim = FuncAnimation(fig, update, frames=times, interval=20)
# アニメーションを保存する
anim.save('scatter.gif', writer='imagemagick')
この記事が気に入ったらサポートをしてみませんか?
