加法定理が腑に落ちた時には、すでに大学受験も過ぎ去っていました(1)

　筆者は高等学校の生徒であった頃から数学が苦手で、例えば三角関数の加法定理というものは証明がどうしても理解できず、あきらめて丸暗記だけして使用しておりました。そしてその状態で何年もふたをして放置し続けていたところ、人生経験？の蓄積が効いたのでしょうか、あるとき突然、何の前触れもなく腑に落ちました。今回はそんな、一番必要な時期を過ぎてしまってからストンと腑に落ちた、青春に間に合わなかったお話です。

三角関数そして加法定理

　筆者は数学が苦手です。大学は理学部物理学科に進みましたが、それでも数学は苦手でした。「でした」と過去形であるのはその後得意になったという意味ではなく、ごまかしが効くようになったり使わないで済むようになってきた、という意味です。
　世間様では三角関数が難しい数学の象徴の様に言われることが多い様です。筆者はそれに賛同はしない立場ですが、しかしそうはいっても数学が苦手な立場の者としては、完全にそういうのから自由というわけでもありません。具体的に言うと、高校レベルの学習で絶対に覚えて使えなければならない有名な公式に三角関数の加法定理がありますが、アレを私は相当程度ずっと丸暗記して意味に目をつぶって単に問題を解くために、受験生であったり大学生であったりした時分に使っていました。
　恥ずかしいことです。
　しかし、高校生であった頃にはその意味がさっぱり理解できなかったので、しかたがなかったのです。
　今でも入口から完全自力で証明しろなどと言われたら裸足で逃げだしますが、しかしそれでも加齢とともに理解・解決に至った諸問題の中に、幸いにも加法定理の理解というのも含まれていました。高度な水準の話でもない、単に定理の意味が腑に落ちる、といった程度のことです。それでも、鼻づまりが一気に通ったかのような爽快感を覚えたことを、今でも憶えています。
　という訳で、どういう理屈ですっきりしたのかの自分語りです。本稿はエッセイ調の文章ですので、自分語り、大いに結構なのです。

座標を回転させると腑に落ちる

　ストンと腑に落ちることができた、その具体的な落としどころの論法が何であったかというのを、最初に明らかにしてしまいましょう。
　様々に提示されている加法定理に関する説明の中の、どういった論法でストンと来るのかは人によって異なると思いますが、筆者の場合には、加法定理が座標の回転変換の和だ、という説明でした。
　これは、そこいらの書物のページをぴらりとめくれば、どこにでも転がっている情報です。
　苦手意識というのは本当に恐ろしいものです。筆者にとっての天啓の様なこの情報を記述する文章とは、おそらく連日ニアミスしながら生活していたにもかかわらず、人生において10年のオーダーでそれを視界に入れようとせず、逃げ続けていたわけです。たまたま加法定理みたいな役に立たない情報（おっと、これはオフレコ）だからよかったものの、もっと生活に密着した情報について、同様の逃避や拒絶で何年も足踏みをしていたとしたら、大変な損失を被っていたかもしれません。
　従ってこの自分語りの前段として必要なのが、まずは高校で学習する座標の回転変換の確認ということになります。

座標の回転変換に関する再確認

　単純な2次元直行座標系$${O}$$を考えます。この座標上のある点$${P(a,b)}$$が$${(x,y)=(a,b)}$$の位置にある場合を図1の様に描いてみます。

図1

　座標の回転とは、$${O}$$と原点が一致して角度$${\theta}$$回転しただけの座標$${O'}$$があった場合、点$${P(a,b)}$$は同時に、$${O'}$$系では$${P(a',b')}$$という座標をとることになりますが、ひとつの点に関する両座標系の関係のことです。図2の様な感じです。

図２

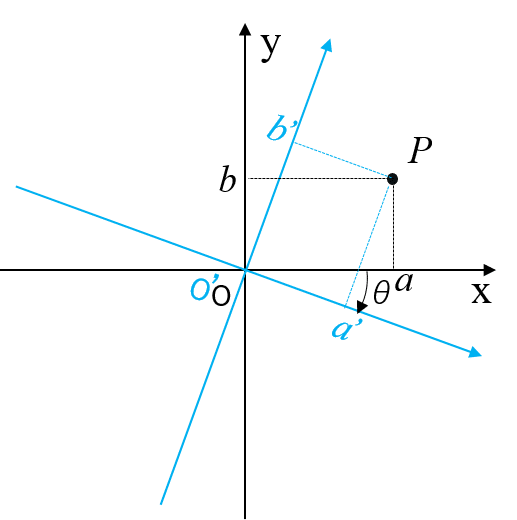
　その様な場合に、点$${P}$$の$${O'}$$系での座標である$${(a',b')}$$を$${O}$$系の座標$${(a,b)}$$で書き表すとどうなるかの変換の式が、回転変換になっています。最終的に、以下の様な形式で変換式を確定させることになります。

$${a'=aとbを含む計算式\\b'=aとbを含む計算式}$$

これは高校で学習された皆さんご承知の通り、回転する座標系の両方が図2の様に重なって表示されている状態で少し考えると、単純に幾何学的に、段々と見えてきます。
　なのですが、字数の関係で次の記事へ続きます。