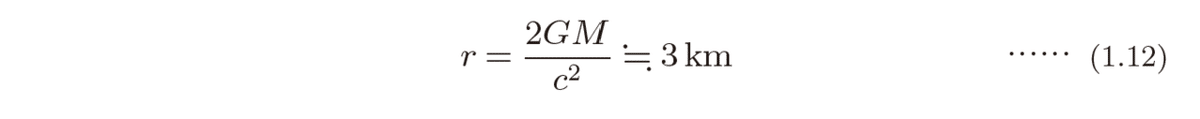「ブラックホールを表す数式」の正体

今年4月、「ブラックホール観測に成功した」というニュースが飛び込んできました。M87銀河の中心にある巨大ブラックホールの「影」が撮像されたというものです。人類が初めてブラックホールの姿を見た瞬間だとして、大きな話題となりました。

物理学者たちは、この偉業が達成されるずっと前から、ブラックホールの存在を知っていました。100年ほど前にはすでに、理論物理学によってブラックホールの存在を示す「数式」が導かれていたのです。いったいどんな「数式」なのでしょうか。

それを理解するためには、「一般相対論」を勉強しなければなりません。一般相対論は、物理学科の大学4年生が「選択科目」として履修するような、難解な科目です。しかし、理論物理学者の小林晋平先生は、そのエッセンスは高校1年生でも理解できると言います。そんな信念のもと書かれたのが、『ブラックホールと時空の方程式：15歳からの一般相対論』です。一般相対論理解への最短ルートを切り開いた、常識破りな一冊となっています。

・「ブラックホールを表す数式」とはいったい何なのか。
・それが「高校1年生でもわかる」とはどういうことなのか。

以下に、同書の要点がつまった「第1章」を公開します。ぜひ、時間のあるときに、じっくりと読んでみてください。

＊＊＊

ブラックホールを「表す」～数式から現れる世界～

著：小林晋平
イラスト：ますとみけい（アトリエ・サルバドール）

1.1　ブラックホールとは？

「ブラックホール」という単語ほどよく知られた科学用語も珍しいでしょう。もちろん、「力」や「熱」のように、科学とは別に日常的に使われる単語はもっとたくさんありますし、原子や細胞、電流や電圧といった科学用語もよく知られていますが、それらは学校で教わる単語です。それに比べ、ブラックホールを学校の理科の授業で扱うことは（まったくないとは言いませんが）ほとんどありません。それにもかかわらず、「ニュートンの運動方程式」や「マクスウェル方程式」といった、物理学でははるかによく使う重要な単語を押しのけて、ブラックホールという言葉は有名です。しかも、ひとたび吸い込まれると光さえ出てくることができない穴のようなもの、というその性質すらも多くの人に知られています。では、ブラックホールについて詳しく知っていますか？と質問されたら、皆さんはどう答えるでしょうか。なぜ光すら出て来られないのか、そんなものが宇宙にあるということがどうしてわかったのか、答えられる方はどのくらいいるでしょう。名前の割に、その実態がほとんど知られていないことも、ブラックホールの特徴なのかもしれません∗1。

∗1　身の回りにある馴染み深いものもすべてそうかもしれませんね。たとえばパソコンのなかでどんな機構が働いているのか、なぜスマホや携帯電話で会話ができるのか、時計のなかはどうなっているのか、高層ビルはどんなメカニズムで支えられているのかなどなど……。考えてみれば、私たちがその仕組みを理解していて、他の人に説明できることって一体どのくらいあるのでしょう？　逆に、自分は知らないけれど、世界中で誰か1人でもいいから理解している人がいるようなことって、どのくらいあるのでしょう？

たとえばブラックホールは、どんな形をしていると皆さんは想像しているでしょうか。私が一般の方向けの科学講座でこの質問をしてみると、「ホール（穴）」という名前がついているからか、宇宙に穴のようなものが空いているというイメージをおもちの方がいました。「宇宙に空いた穴」というのはある意味正しいのですが、形としては「穴」というより、星のような球形をしていると考えられています。宇宙空間に浮かぶ、球形の特殊な領域です。

ブラックホール、今と昔
「ブラックホールといえば相対性理論」というイメージをもっている人も多くいるようですが、「光すら脱出できない天体が存在するかもしれない」というアイデアが最初に登場したのは18世紀末のことです。イギリスの天文学者ミッチェルやフランスの数学者ラプラスが考えました。一方で、アインシュタインが特殊相対論を発表したのが1905年であり、本書のテーマである一般相対論を完成させたのは1915年のことです。翌1916年には、その一般相対論を使ってドイツの天文学者シュヴァルツシルトによってブラックホールを表す「解」が初めて発見されました。ということは、その100年以上前から科学者たちは、ブラックホールという名前こそなかったものの、光すら逃げられない特殊な天体が宇宙にあるかもしれないという可能性について考察していたことになります。

さて、一般相対論の発表から100年以上が経った現代では、ブラックホールだと考えられている天体が非常に多く見つかっています∗2。ブラックホールには太陽の数10倍程度の質量のものから、銀河の中心に存在する超大質量ブラックホールまで、いくつかの種類があります。私たちの太陽系は天の川銀河に含まれていますが、その中心にも「いて座A∗」という、太陽のおよそ400万倍もの質量をもつ巨大なブラックホールがあると考えられています。大抵の銀河の中心に巨大なブラックホールが存在していると考えられているのですが、地球から観測できる範囲だけでもおよそ1000億個の銀河があるため、巨大ブラックホールもそれと同じくらいの数だけ存在していることになります。また、銀河にもさまざまな種類があり、そこに含まれている星の種類もさまざまですが、天の川銀河には2000億個もの恒星（太陽のように核反応で自ら光っている星）があります。それらのなかには非常に重いものがあり、そうした恒星は進化の果てにブラックホールになると考えられるため、そうした星由来のブラックホールもそれぞれの銀河に存在しているはずです。ブラックホールは、実はありふれた天体でもあるのです。

∗2　Wikipediaに「ブラックホールの一覧」という項目があるほどです。

ブラックホールは「見えない」
ところで、ブラックホールだと「考えられている」天体という、奥歯に物が挟まったような言い方をしているのはなぜでしょうか。それは、ブラックホールそのものを目で見ることはできないからです。それが「ブラック」と呼ばれる理由ですが、「光が出て来られない＝ブラック」とはどういうことかを理解するために、「物が見える」とはどういうことなのかを少し詳しく説明しましょう。

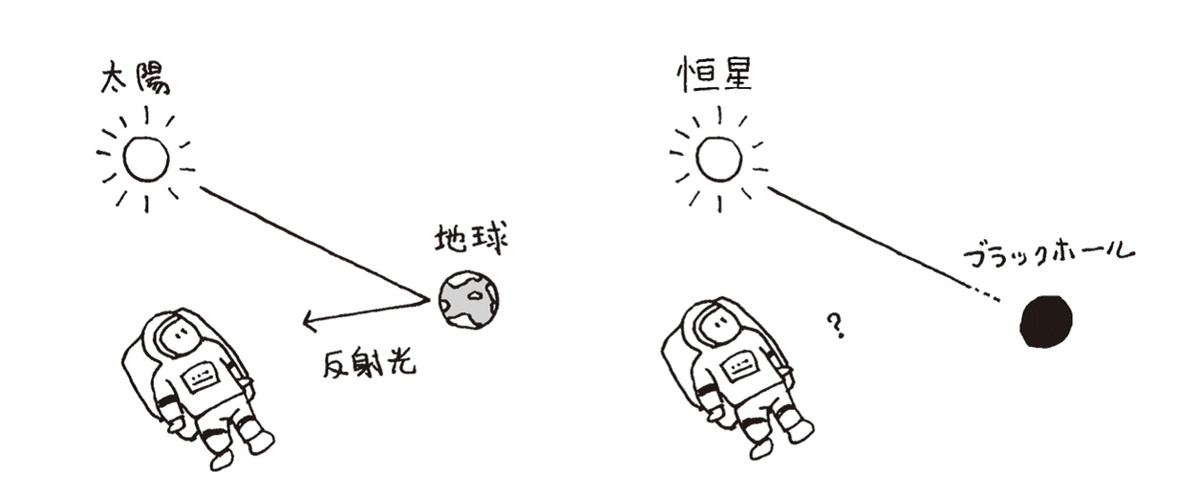
たとえば、明かりを消した真っ暗な部屋のなかにボールが置かれているところを想像してください。明かりがないのですから、当然ボールは見えません。これは、ボールが自分で光っていない、つまり光を発していないからです。ボールを見たければ、懐中電灯などで光を当ててボールを照らさなければいけません。懐中電灯で光を当てると、その光はボールの表面で反射し、私たちの目の奥にある網膜に届きます。網膜には光を感じ取る細胞があるので、そこに光が届くことで「あそこにはボールがある」とわかるわけです∗3。燃えているロウソクのように、自分から光っている物体であれば暗闇でも見えますが、自ら光っていない物体を見るためには懐中電灯などで照らし、反射光を私たちの目に届かせる必要があるのです。では、もし懐中電灯から発せられた光がそのボールに吸い込まれてしまい、一切反射されないとしたらどうなるのでしょう。いくら光で照らしても、すべて吸収されて全然反射しない、「のれんに腕押し」状態です。この場合、私たちの目に反射光が届かないのですから、そこにボールがあるかどうかはわからなくなってしまいます。ブラックホールとは、そのような、光を吸い込むばかりで一切反射しない天体なのです。この性質のため、宇宙の闇のなかで他の星からの光線がいくらブラックホールを照らしても、月や地球のように明るく照らし出されることはありません（図1.1）。私たちの目には何の姿も映らず、真っ黒に見えます。これが「ブラック」という名前の由来です。本書の最後では、ブラックホールは一方的に光を吸い込むばかりで、中からは光も脱出できないことを確かめます∗4。

図1.1 　惑星は恒星に照らされ、その反射光によって私たちから見える（左）。恒星からの光を吸い込んでしまう天体は、光を反射しないのでいくら照らしても見えない（右）。

∗3　桿体細胞と錐体細胞という2種類の細胞があります。とくに桿体細胞は暗いところでの感度がよく、光をキャッチすると、そのエネルギーによって細胞内で化学反応が起き、電流が流れます、それに基づいて、脳内で目が見たものを映像に置き換えるのです。見ることに限らず、嗅ぐ・触るといった私たちの五感に関わる現象は、突き詰めていくと化学反応によって発生した電気信号が脳に見せている「バーチャル・リアリティ（仮想現実）」です。

∗4　光がブラックホールに吸い込まれるか、その脇を通って逃げていけるかは、光とブラックホールの距離やどんな角度でブラックホールに近づくかによって大きく変化します。

ブラックホールを「見る」
さて、ブラックホールが光を吸い込むばかりで「ブラック」な天体なら、どうやってブラックホールの存在を確認したらよいのでしょう。一つには、ブラックホールの強い重力によって周囲を通る光の軌跡がねじ曲げられ、光源となる天体の像そのものや、いくつかの天体の並びが変化して見える可能性があります。たくさんの星の集団のなかに、ポッカリと黒い穴の空いた「影」が見えるかもしれないのです。このように、ブラックホールがあるとその周囲にさまざまな「ブラックホールが存在すると考えられる状況証拠」が現れます。

歴史上、最初に見つかったブラックホールの候補天体は、はくちょう座X-1と言います。はくちょう座の首の真ん中辺りにあり、X線を出していることからこう呼ばれました。そのように、多くのブラックホールについては、近くにある天体からのガスがブラックホールに吸い込まれる前にブラックホールの周囲で回転し、その際にX線などの強い電磁波を発します。それをキャッチすることで「あそこにブラックホールがあるはずだ」と当たりをつけることができます。この場合も、明るく輝くガスの中に、ブラックホールの「影」が映る可能性もあります。

もっと直接的にブラックホールを「見る」方法もあります。それは、重力波を使う方法です。2015年の2月に、初めて重力波が検出されたというニュースが世界中を駆け巡りましたが、これは地球から13億光年離れたところにある二つのブラックホールが合体するときに出された重力波だと考えられています。

ブラックホールが存在するとその周囲の時空が歪み、その歪みが地球にも届くことがあります。「時空の歪みとは何か？」はまさに本書のテーマですのでおいおい説明していきますが、大事なことは、重力波はブラックホールから発せられた直接的な信号だということです。今後、重力波の観測はますます盛んになり、ブラックホールや宇宙そのものの性質がより詳細にわかっていくと期待されています。事実、2017年8月には、二つの中性子星という非常に高密度の星が合体する際に放出された重力波も検出されました。可視光や紫外線など、従来の望遠鏡による観測に加え、重力波観測も合わせたいくつもの手段で宇宙からメッセージを受け取る、言わば「マルチメッセンジャー天文学」時代がついに到来したのです。

1.2　ブラックホール時空を数式で表す

ブラックホールの数式（シュヴァルツシルト解）を「鑑賞する」ところで、先ほど私は「ブラックホールは一般相対論の解として見つかった」と言いました。「解」と言うからには、何らかの方程式を解いた結果、その答えとしてブラックホールが見つかったということになりますが、一体何を計算したらブラックホールが「見つかる」のでしょう。「ブラックホールについて計算する」と言われて、皆さんはイメージが湧くでしょうか？　ためしに次の数式を見てください。

ブラックホールにもいろんな種類があるのですが∗5、これはボールのように球形をしていて、静的なブラックホールを表す数式です。静的とは、一切の運動をしておらず、ジッと止まっているという意味です∗6。これが一般相対論を用いて歴史上初めて導かれたブラックホール「解」で、導いた人物の名前をとってシュヴァルツシルト解と呼ばれています。シュヴァルツシルト解で表されるブラックホールがシュヴァルツシルト・ブラックホールです。

∗5　現実に存在するかどうかは別にして、理論的にはさまざまな種類のブラックホールが考えられています。

∗6　現実のブラックホールの多くは回転していると考えられ、数式を導いた人の名前を取ってカー・ブラックホールと呼ばれています。カー・ブラックホールを表す数式は式(1.1)に比べ、だいぶ複雑です。

さて、皆さんはこの数式を見て「これはたしかにブラックホールだ」と感じるでしょうか？　一般相対論をまったくご存じない方で、この数式からブラックホールを感じられる方がいるとしたら、相当のセンスの持ち主かもしれません。ちなみに私は初めてこの式を見たときに「おお、ブラックホール！」とは思えませんでした（笑）。それが当たり前だと思いますが、私たちがブラックホールに対して抱いている「宇宙に浮かぶ暗黒の天体」というイメージは、この数式をただ眺めていても全然伝わってきません。一体、この解は何をどう表していて、どこからブラックホールの性質がわかるのでしょう。そもそも、「ブラックホールを数式で表す」とはどういうことなのでしょうか。

複雑な数式の本質を捉える
この式がなぜブラックホールを表す式だと言えるのか、順を追って説明したいのですが、それにしてもシュヴァルツシルト解は複雑です。パッと見ただけで、すぐに内容がわかるようなものではありません。

実を言うと、私たち研究者にとっても、複雑な数式はあまりありがたいものではありません。シンプルなほうがもちろんわかりやすいですし、複雑であまり綺麗でない式を見ると、「もっとうまい書き方が本当はあるんじゃないのか？」という気がします。私たちの日常でも、よく理解できていないせいで回りくどい説明をしてしまうことがありますが、数式もそれと同じで、「まだ理解が浅いから、こんな複雑にしか書けないのではないか？」という気がするのです∗7。

∗7　もちろんこれは半分は「真理はシンプルであってほしい」という私たちの願望です。そして往々にして現実は甘くありません。

とはいえ、単純には表せないものも現実世界には山ほどあります。残念ながら、私たちに理解しやすいよう、自然現象がシンプルになってくれるわけではありません。ではそんな複雑怪奇な現実世界に、私たち物理学者はどうやって立ち向かうと思いますか？

当たり前すぎて申し訳ないのですが、簡単な例から始めて、少しずつ複雑に、現実へと近づけていきます。「え？それだけ？」と拍子抜けされたかもしれませんが、残念ながら「物理学を用いる」と言っても何か特別な方法があるというわけではないのです。割り算の前に掛け算を、掛け算の前に足し算を学ぶ必要があるように、複雑なものを理解するには簡単なところから積み上げていくしかないのですね。これは小学校の勉強でも、最先端の研究でも変わらないのです∗8。

∗8　高校で初めて物理を学ぶとき、物理の問題には「摩擦は無視してよい」とか「空気抵抗は無視できるものとする」と書いてあることが多いことに気がつきます。「摩擦がないなんて非現実的だ。物理は日常とはかけ離れた理想的な世界の話しかしていないのだ」と感じ、物理は定期試験や受験で使うだけの、現実には役に立たない道具だと思っている人も多いようです。物理のさまざまな場面でこのような極端な状況を考える理由は三つあります。一つ目は、すべての要素を取り入れた計算をしたくても、（少なくともはじめのうちは）難しくて計算できないから。二つ目は、現実の場面でも摩擦や空気抵抗がほとんど影響しないとか、影響を与えてはいるけれども測定の限界を超えていて、測ることができないことがあるから。そして三つ目は、現実にはちょっとあり得なそうな極端な世界を考えるのが面白いからです。往々にして物理屋は、極端な状況設定を好む傾向があります。

「簡単なところから始めてだんだん難しくしていく」、当たり前すぎてガッカリしたかもしれませんが、実はこの考え方、非常に強力です。具体的にそれをお見せしましょう。

シュヴァルツシルト解の「枝葉」を落とす
再び先ほどのシュヴァルツシルト解を書きます。

たしかにこの式は複雑です。皆さんに馴染みのない記号もたくさん書かれていると思います。このままではブラックホールの姿はイメージできませんが、この式のどこかに、ブラックホールの本質が潜んでいるはずです。それを抜き出すために、私たちが混乱する原因となる「複雑なもの」を削ぎ落として、簡単にしてしまいましょう。この式を複雑にしている理由はさまざまありますが、まずは項の数が多いことに注目しましょう。項が多いとどこが本質なのか一目見ただけではわからなくなりますから、どこかの項を消してみましょう。どうせ消すなら難しそうなものから消すことにします∗9。

∗9　「え？難しいところこそ意味があるんじゃないの？」と思った方もいるかもしれませんが、そうとは限りません。本質は極めて単純なのに、細かい条件がついているせいで複雑になっていることはよくあります。もし消しすぎてしまって何にもなくなってしまったら、また戻って一からやり直せばいいだけのことです。

左辺はすっきりしていますから放っておき、右辺を見ると、項が四つあります。そのうち最初の項にだけマイナスがついていますね。プラスとマイナス、足し算と引き算であれば引き算のほうが難しく感じられるでしょうから、マイナスがついたd(ct)^2の項を消しましょう∗10。すると

となります。「勝手に消していいの？」と思われる方も多いでしょうが、これは物理的なプロセスではなく、対応する現実的な過程があるかどうかはひとまず無視しています∗11。この解の本質を見抜くための特殊な操作ですので、「いきなり消す」というのはたしかに普通ではないことをやっていますが、気にせず進みましょう。さて式(1.2)ですが、これでもまだ複雑です。とくに右辺第1項には1−2GM/(c^2 r)を分母にもつ分数が入っています。分数と整数、ややこしいのは分数のほうですから、この分数の分母部分を消してみましょう。すると

となります。

∗10　この話を小学生向けの講座でも話したことがあるのですが、「足し算と引き算、どっちが簡単？」と聞いたところ、小学4年生の子に「場合によります」と言われました。まったくそのとおり。

∗11　dtという量が0なら現実にこの状況が起こります。つまりdt=0とおくということは、実際にこれに対応する物理的状況が存在するものです。ただし、これ以上の細かいことは先の章に譲り、ここでは述べません。

だんだんすっきりしてきました。この式の右辺には項が三つありますが、実は三つの項があることは、空間が3次元であることに由来しています。私たちが住むこの世界は3次元なので、項が三つあるほうが自然ですが、3次元と2次元、簡単なのは2次元の平面のほうですから、さらにもう1項消しましょう∗12。3次元は空間図形の世界、2次元は平面図形の世界ですが、空間図形をある角度から切ったら断面がどうなるかとか、平面図形に比べると空間図形を頭に思い描くのは大変ですよね。さっきと同じように、どうせ1項消すならややこしそうなものを消すことにして、三角関数のsinが入っている項を消すことにしましょう。すると

となります。当初のシュヴァルツシルト解と比べると、非常にシンプルになってきました。

∗12　本当にこの世界が3次元空間なのか、それについては後の章でお話しします。

どこかで見たことがある式に……
さらに簡単にしましょう。どこをいじるかですが、ここで皆さんに質問です。東京と京都、どちらが複雑でしょうか？

妙な質問ですね。答え方はいくらでもありそうです。この意図は、図1.2にあります。そう、東京と京都の道路の様子です。

図1.2　東京と京都の道路の比較。東京は極座標的、京都はデカルト座標的である。

ご存知のように、平安京の名残りである京都の町並みは「碁盤の目」とよく言われます。この道路の張り巡らされ方は、数学的には直交座標に対応しています。直交座標とは、私たちは中学のころから馴染みのある座標で、互いに直交するx軸とy軸を張り、それぞれの軸の目盛りでもって物体の位置を表示する方法です。直交座標は、この表示法を導入したのがデカルトであることから、デカルト座標とも呼ばれます。本書では、これ以降、デカルト座標という呼び方のほうを用いることにします∗13。さて、デカルト座標では、たとえばxの読みが3、yの読みが2なら、点の位置を(3,2)のように表します。京都では、交差点の名前を東西の通りの名前と南北の通りの名前を合わせて表しますが、これこそデカルト座標的な表示方法です。たとえば京都で一番の繁華街は四条河原町という辺りですが、この名称はこの場所が東西に走る四条通と、南北に走る河原町通の交差点であることを示しています。つまり、

（四条, 河原町）

のように、デカルト座標的に地名を表示しているのです。

∗13　厳密に言うと、直交座標のほうが広い概念であり、デカルト座標はその一種です。

一方、東京の道路網は碁盤の目とはまったく違った形をしています。こちらは環七や環八のように、皇居を中心とする同心円の環状道路と、皇居から伸びる放射線状の道路とで構成されています。これは数学的に見ると極座標と呼ばれる座標の張り方と同じ形です。

極座標とは、ある点を中心とし、物体の位置をその点からの距離rと、ある軸（図1.3ではx軸）からの傾きの角度θで表す表示法です。東京の道路で言うと、半径rが環状線の番号に対応し、θが放射状に伸びる道路のうち、どの道路なのかを表すことになります。

極座標はデカルト座標とは見かけは異なりますが、本質的には同じものとも言えます。なぜなら、どちらの座標も「物体の位置を表現する」という意味では同じように機能しているからです。私は群馬に住んでいた頃、車で上京する際に必ず豊玉陸橋という場所を通っていました。ここは環状7号線と目白通りの交差点です。座標風に書けば

豊玉陸橋 =（環七, 目白）

となります。極座標による場所の表示です。このように、物体の場所を表す方法にはさまざまなものがあり、その時々に応じて便利な座標を使うことができます。では再び数式に戻りましょう。先ほど見た式(1.4)ですが、実はこの式、右辺が極座標で書かれています。極座標では図1.3のように半径と角度で物体の位置を表すと言いましたが、式(1.4)右辺のrは、radius、すなわち座標原点からの半径であり、θは水平方向（普通、x軸の正方向にとる）から測った角度を表しているのです。式(1.4)が何を表す式なのかはまだ不明ですが、とにかく式(1.4)の右辺が極座標で書かれているということだけ、まずは了承してください。

図1.3　極座標では、原点からの半径rと、x軸からの角度θで物体の位置を表す。

先ほどから述べているように、物体の位置を表すのに極座標を使っても、デカルト座標を使っても本質は変わりません。そもそも座標とは、私たち人間が何かを計算するために便宜的に導入したものだからです。地球の表面に経線や緯線が描いてあるわけではないのと同じで、物理的実在と座標とは本来関係ありません。位置に限らず、あらゆる物理現象はどんな座標を使っても原理的には表せます。

同じことが式(1.4)についても言えます。式(1.4)は極座標で書かれていた「何か」なのですが、これにもデカルト座標で書いたバージョンがあるのです。その具体的な形は

です∗14。さて、ここまで来ると何だかどこかで見た数式のような気がしてこないでしょうか。この数式の正体がわかるまで、あと一歩です。

∗14　ここでは天下り的に与えましたが、なぜこのようになるのかは後の章で説明します。

ラストスパートとして、この数式に最初からずっと入っている「d」を見てください。何だかよくわからないので、これも消してしまいましょう∗15。すると

となります。

∗15　もちろん「d」の意味も、後の章でご説明します。

どうでしょう？　これが何の式か気づかれた方も多いのでは？　文字に何か具体的な数値を入れてみれば、さらに明らかになります。たとえば、

としてみましょう。これはよく知られた式ですね。そう、これは三平方の定理です。すなわち、直角三角形の縦の辺の長さが3、横の辺の長さが4であるとき、斜辺の長さは5であり、その三つの数の間には式(1.7)が成り立つ、というものです。つまり、これまで扱ってきた数式は、三平方の定理に関係していたのです。

式(1.1)の本質は……
三平方の定理（別名ピタゴラスの定理）は、平らな面に置かれた直角三角形の、縦・横・斜めの辺の長さの間に成り立つ関係を表しているわけですが、言い方を変えると、平らなところで離れた2点間の距離ABを出すのに使える定理でもあります（図1.4）。

図1.4　直角三角形について成り立つ三平方の定理。3^2+4^2=5^2である。

ここで、私が突然「平ら」を強調し出したことにお気づきでしょうか。なぜ急に「平ら」などと言ったのでしょう。もし平らでないなら、どうなるというのでしょう。ためしに、平らでないところだと何が起きるのか考えてみましょう。平らでない面の例として、地球の表面を想像してください。今あなたが北極点にいるとして、そこから経線に沿って南下し、赤道まで歩いてください。赤道に到着したら90度向きを変え、今度は赤道に沿って進んでください。しばらく歩いたら、どこか適当なところで再び90度向きを変えて北を向き、経線に沿って北極点を目指してください。このとき、あなたが動いた軌跡を見てみましょう。それは曲線で囲まれた三角形になっているはずです。しかしこの三角形、ちょっと妙です。よく見ると、赤道で向きを変えたところに二つ直角があります。これは普段あまり見かけない三角形です。試してみればすぐにわかるように、直角を二つもつ三角形を平面上に書くことはできません。三角形の二つの辺が互いに平行になってしまい、交わらないからです。しかし、地球の表面のように曲がった面では事情が変わってきます。表面の曲がりのおかげで、図1.5のように平行線が北極点で交わるのです。うまくやれば北極点で直角に線が交わるようにもできますから、直角を三つもつ三角形をつくることもできます。

図1.5　地球の表面に書いた三角形。赤道と経線は直交する。このように、二つ直角をもつ三角形も球面上なら存在できる。

このような、「曲がった図形」まで考えた幾何学を非ユークリッド幾何学と呼びます。非ユークリッド幾何学には、普通（すなわちユークリッド幾何学）とは違った直角三角形がたくさん出てきます∗16。

∗16　「普通」というのは、所詮私たちがこれまでの人生で比較的多く目にした程度の意味しかないと思うのです。地球の表面に描かれた曲がった三角形と、平らな紙の上に描かれた三角形、果たしてどちらが普通で、どちらが特殊でしょうか。

直角三角形がそもそも違うのですから、非ユークリッド幾何学における直角三角形については、三平方の定理も私たちが中学で教わる形をしていません。このことは、地球の表面のような曲がったところでは、離れた2点間の距離は「普通の」三平方の定理では書けないということを意味します。地球表面のような滑らかな面ですら、曲がっている場合には奇妙な直角三角形が現れるのですから、ましてブラックホールのような「穴」の空いた妙な空間では……？

そうなのです。シュヴァルツシルト解から出発した式が、いつの間にか三平方の定理になったのは、最初にお見せしたシュヴァルツシルト解が、

「通常の三平方の定理が成り立たないような奇妙な空間における、2点間の距離を表す式」

だったからなのです。そしてあの式が三平方の定理とどう違っているか、そこにこそあの式がブラックホールを表す理由が含まれていたのです。

1.3　数式から読み取れる物理

式(1.1)には、ブラックホールの性質を示す情報が含まれています。詳しくは第8章に譲るとして、ここでは少しだけ見てみましょう。

ブラックホールの半径
先ほど、シュヴァルツシルト解のrは半径（radius）のrであると言いました。式(1.1)を見ると、右辺第1項と第2項に共通の

という式がありますが、この式はもしrが

ならばゼロになります。つまりrがこの値（シュヴァルツシルト半径と言います）のとき、右辺第1項はゼロになり、第2項に至っては分母がゼロになります。したがって、この半径はシュヴァルツシルト解にとって特別な値であり、これには何か意味がありそうです。

ところで、これらG、M、cはそれぞれ、万有引力定数、質量、真空中の光の速さを表す記号です。万有引力定数とは、二つの物体の間に働く万有引力の強さを決めている比例定数で

という値です。真空中の光の速さは相対性理論では極めて重要な量ですが、その値は

です。実に1秒間に地球を7周半もするという、凄まじい速さです。これらの値に加え、Mとしては太陽の質量M=2×10^30 kgを考えてみると

という値になります。

突然ですが、このことは

太陽を半径3kmに圧縮すると、ブラックホールになる

ことを意味しています（図1.6）∗17。シュヴァルツシルト解が異常になる場所、すなわちr=2GM/c^2地点はブラックホールの表面と考えられるのです。シュヴァルツシルト半径とは、（そう考えられる理由や、なぜ光ですらそこから脱出できないかについてはまだ何も説明していませんが）ブラックホールの半径のことなのです。ここで改めて最初のシュヴァルツシルト解を眺めてみてください。

どうでしょうか。最初に見たときと、少し印象が変わっていないでしょうか。少なくとも、dr^2などの2乗の部分は、三平方の定理の2乗のことだと見えてはこないでしょうか。分数の部分もただの複雑な項というだけでなく、「あそこが0になるようなところがブラックホールの表面なのか」と、深い意味がどことなく感じられてはこないでしょうか。このように、数式には物理が隠れています。その意味で、数式は言葉だとも言えます。文法やボキャブラリーを増やさなければ理解できないという意味でも、数式は言葉と同じです∗18。

図1.6　太陽の半径は地球の約110倍の70万km。これを半径3 kmに圧縮できたらブラックホールになる。

∗17　太陽の質量は2×10^30 kgですが、これでは軽すぎて（！）、太陽が燃え尽きる際に重力崩壊という現象を起こしても、ブラックホールにはなりません。太陽質量の20～30倍以上の質量をもつ星でないと、その一生の最後にブラックホールになることはないと理論的には考えられています。

∗18　生まれ育った国で24時間聴き続けている言語なら、文法をしっかり学ばなくても話ができるようにはなります。それに、文法を少々外れた話し方をしても、周りの人は頭のなかでそれを補完して理解もしてくれます。しかし数学という言語はそうはいきません。間違った使い方をしたらまったく意味が通らなくなってしまうのです。このため、直感やイメージで「何となく」理解することは大変重要ではあるものの、きちんと「数学の文法」も学んでおく必要があります。

さて、私は複雑な式の枝葉を適当に落としていくことで、シュヴァルツシルト解の式の本質が三平方の定理にあることをご説明しました。この「余分なものをどんどん削ぎ落とす」という方法は物理学ではよくやる手ですが、「本質に目をつけ、残りの枝葉は落として考える」というのはあらゆる場面で役立つ手段でしょう。その際には、何に注目したらよいか、そして何が本質なのかを見抜かなければなりませんが、「はじめに」でも述べたように何が本質なのかは目的によって変わります∗19。そのため、一概に「ここに注目せよ！」と言い切ることは難しいのですが、「変わらないもの」に注目することが重要になることは多いと言ってよいでしょう∗20。これも後の章で取り上げる話題ですが、「変わらないもの」がなぜ変わらないのか、実はその背後に自然の美しさがあります。ここで言う美しさとは、数学的には対称性と言われるもののことです。変わらないことを物理では「保存する」と言いますが、たとえば力学的エネルギー保存則のような、成り立つのが当たり前に思える有名な保存則も、成り立つ理由があります。それが自然界がもっている対称性という性質なのです。この意味で、物理的なモノの見方、すなわち物理では何に注目するのか、そしてどうやって注目するのかを知ることは、自然がいかに美しいかを知るための方法にもつながるのです。その意味では、複雑に見えるシュヴァルツシルト解も、実は高い対称性をもっており、すでに「美しい式」ということもできます。物理学があらゆる理系の学問の根底にあることはよく知られていますし、だからこそ理系にとって物理は必須の学問であるとも言われます。しかし私個人としては、そんなこと以上に、物理学が見つめているものの先にある、私たちを取り巻く世界の美しさ、そしてそれを求める人間の営みを知ることが、物理を学ぶ最大の価値であると思っています。

∗19　もっと言えば、「本質を見抜くこと＝自分が何をしたいと思っているのかを知ること」でもあります。つまり、自分が何を欲しているのかがわからなければ、本質を見抜くことはできないのです。

∗20　シュヴァルツシルト解で書いていたdsという量は世界長さと言われ、不変量と呼ばれるものの一つです。「不変」とはどういう意味か、何に対して不変なのかは後ほど説明します。

1.4　本書の構成

さて、本章ではシュヴァルツシルト解の本質を見抜くために枝葉の部分をどんどん削ぎ落としていきました。逆に言うと、あの解がブラックホールを表す式であって、単なる三平方の定理ではない理由は、その枝葉の部分に入っていることになります。よって、すべての幹となる三平方の定理をまずは理解し、あとは先ほど私が式を変形していったのと逆の順で枝葉をつけ直していけば、ブラックホールが現れてくることになります。

私が先ほど式変形を行った内容を整理してみると

　1.　マイナスがついていた項を落とした
　2.　分数部分を落とした
　3.　sinの項を落として3次元から2次元にした
　4.　極座標をデカルト座標にした
　5.　dという記号を外して三平方の定理の形にした

となります。このそれぞれは

　1.　空間に時間を加える（4次元時空を導入する）→第5章
　2.　1−2GM/(c^2 r)の出どころを理解する（アインシュタイン方程式を解く）→第7、8章
　3.　2次元や3次元など、さまざまな次元の空間の図形を扱う（いろいろな次元の幾何学を考える）→第4、6章
　4.　デカルト座標から極座標など、複数の座標を行き来する（座標を変換する）→第3章
　5.　有限の大きさから、微小量・無限小量へ移行する（微分や積分を実行する）→第2章

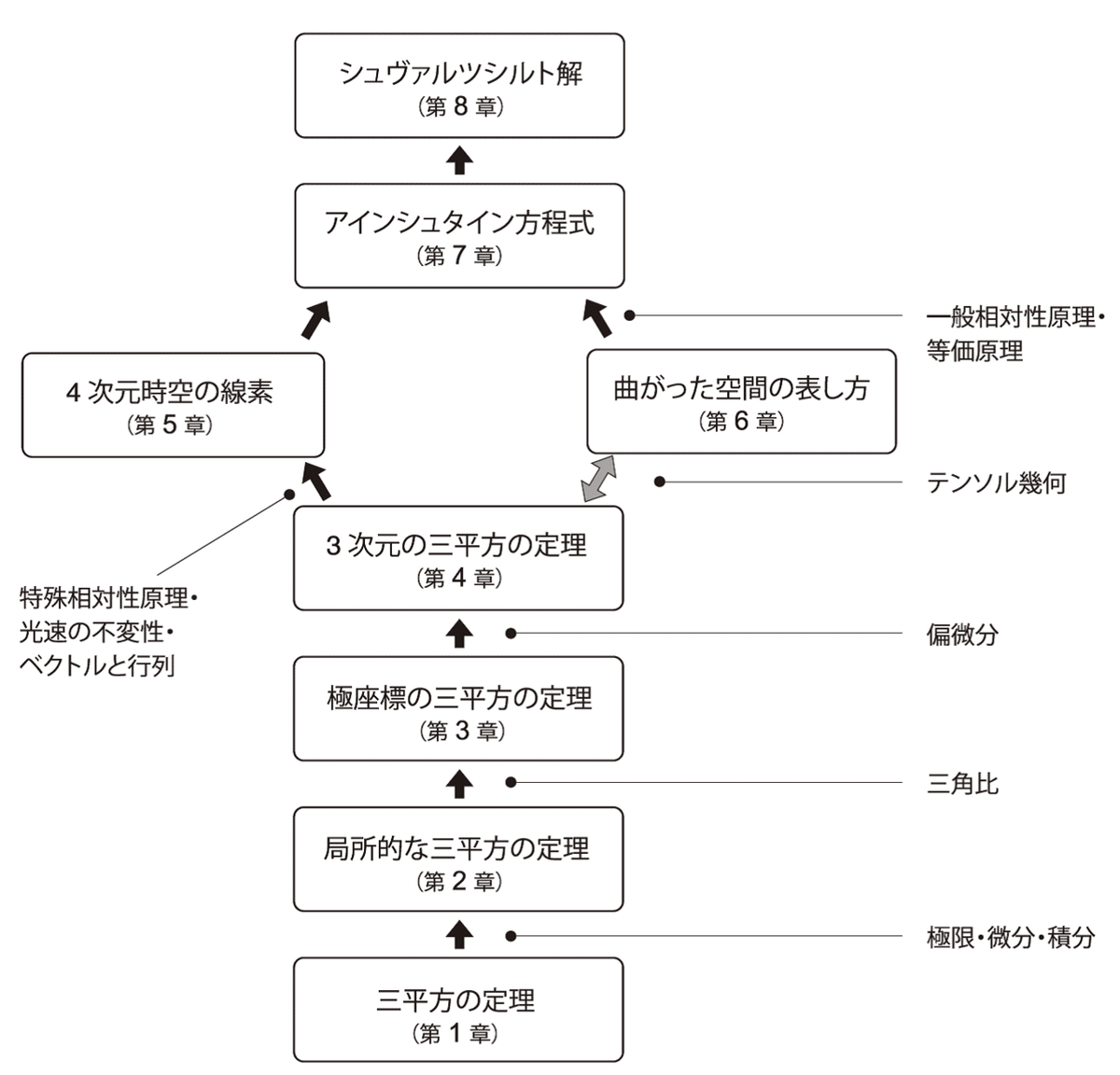
というテーマに対応しています。つまりこれらを押さえることで、最速でシュヴァルツシルト解、すなわち相対性理論からブラックホールが数式として導かれていく様を理解することができるのです。では次章から具体的にこれらパーツの一つひとつを揃えていきましょう。章ごとにパーツを一つずつ揃えていくことになりますが、実はパーツの一つひとつは微分積分・三角比・行列・偏微分といった、高校や大学で学ぶ数学のそれぞれに対応しています。高校や大学で学んできた数学は何を表していて、何の役に立つのかにも注意して読んでいただければ、数学と物理が互いに協力し合って発展してきた歴史を味わうこともできるかと思います。

図1.7　本書の構成と各所で登場する数学。

出典：『ブラックホールと時空の方程式』第1章

小林晋平（こばやし・しんぺい）
1974年長野県生まれ。東京学芸大学教育学部准教授。相対論、宇宙論、量子重力を専門とする理論物理学者。2004年、京都大学大学院人間・環境学研究科博士課程修了。博士（人間・環境学）。東京大学大学院理学系研究科附属ビッグバン宇宙国際研究センター研究員、日本学術会議海外特別研究員（カナダ・ウォータールー大学およびペリメーター理論物理学研究所にて研究）、群馬工業高等専門学校准教授を経て、2015年より現職。群馬高専では6年連続して学生からベストティーチャーに選出される。相対論・宇宙論・量子論をわかりやすく解説する一般向け講座を多数開催している。

＊＊＊
『ブラックホールと時空の方程式：15歳からの一般相対論』

物理学者は，いかにして現象を記述し，世界を見るのか？
「ブラックホールを数式で表す」とは，いったいどういうことなのか？
高校数学から出発し，「一般相対論」へと一気に駆け上がる，
本気の物理学を知るための独習書．

【推薦の言葉】
ブラックホール時空への直通の登頂路！　友人や，物理や数学の先生と一緒に登れば，なお楽しい登山になるに違いない．―― 橋本幸士（物理学者，『「宇宙のすべてを支配する数式」をパパに習ってみた』著者）

たった一行の方程式を理解する経験が，どれほど豊かなことかを教えてくれる．―― 森田真生（独立研究者，『数学する身体』著者）

【目次】
第1章　ブラックホールを「表す」：数式から現れる世界
第2章　距離を測る：線素と微分積分
第3章　測り方を変えてみる：デカルト座標から極座標へ
第4章　次元を上げる：偏微分と3次元極座標
第5章　「時間と空間」から「時空」へ：特殊相対論
第6章　空間の曲がりを表現する：ベクトルと曲率
第7章　重力は時空の曲がりである：一般相対論
第8章　ブラックホール解を導く：アインシュタイン方程式とシュヴァルツシルト解