
ChatGPTは数式を理解してくれます。解いてもくれます。LaTexでもOK。むしろLaTexを出力させてラクする。
理解というか、グレブナー基底的に代数方程式を把握してくれるに近いけれど。
ChatGPTさんは、数式をLatex記法で書いても分かってくれます。Latex記法のそのものがマークアップ言語なので、自然言語処理できるからです。
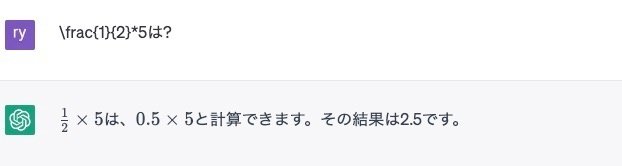



もっと高度なこともしてくれます。
わたしは検算していませんけど、ざっと見た感じで「たぶん」あってる。
計算過程をさらに詳細に出力することもできる。
学習者が「さらに詳しく聞きたい」ときに使える。
このようにChatGPTは驚くべき挙動をしてくれます。使う公式まで出してくれて、これは先生や本がいらなくなのかもしれません。
しかし、注意しておきたいのは、
突拍子もなく、平然と間違えてくれる。
現時点「探してきた回答を数式を理解せずにコピペしている」と同じだと思います。
間違えるときを予想できない。訊き方、タイミングによっては正しい回答をするときもある。
分数の計算でもタイミングによっては間違えます。
結局は、検算を自ら行い、人間側が正誤を確認するしかありません。

このようなChatGPTの側面を使えば、数学(理工学)分野とプログラム言語に関しては、書籍がいらなくなります。
たとえば、知りたいIT技術、分野について、
ChatGPTで目次やアジェンダを取得する。
目次やアジェンダから、詳細に項目を書き出してもらう。
とすればいいのです。
ただし、人文系の回答にはChatGPTの「でまかせ」があります。人文系などでは、ChatGPTでは代替できません。人文系での用途ではChatGPTでは嘘だらけです。
このことから、現在の人工知能の限界点がわかります。
つまり、このChatGPTの振る舞いが、すべての分野で人間の知性を完全に再現しているわけではない、ということです。
ChatGPTは、人間による人力の文書から、学習しています。依然として、人がデータ(文書)を生成することはクリエイティブな活動として継続されていきます。
ChatGPTのLaTex出力は便利です。
つぎのような式を書くときに、「上手く訊いて」出力してもらいます。
LaTexを使う方なら、人力で書く面倒さを、おわかりいただけるはず。
$$
\frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial u}{\partial r} \right) + \frac{1}{r^2 \sin \theta} \frac{\partial}{\partial \theta} \left( \sin \theta \frac{\partial u}{\partial \theta} \right) + \frac{1}{r^2 \sin^2 \theta} \frac{\partial^2 u}{\partial \phi^2} = 0
$$
とか、
$$
R_{\mu\nu} - \frac{1}{2} R g_{\mu\nu} = 8\pi G T_{\mu\nu}
$$
$$
R_{\mu\nu} = \partial_{\alpha}\Gamma^{\alpha}{\mu\nu} - \partial{\nu}\Gamma^{\alpha}{\mu\alpha} + \Gamma^{\alpha}{\beta\alpha}\Gamma^{\beta}{\mu\nu} - \Gamma^{\alpha}{\beta\nu}\Gamma^{\beta}_{\mu\alpha}, R = g^{\mu\nu} R_{\mu\nu}
$$

この記事が気に入ったらサポートをしてみませんか?
