マニアックなことも理解できる授業。鳩の巣原理:オモワカ整数＃21(全21回)

整数シリーズ第２１回目！！ラストです！！
オモワカ＝面白いほどわかる
整数が面白いほどよくわかります
第２１回から見てもOKですが、ぜひ第１回目からどうぞ！！　→→　１回目（倍数の判定）

鳩の巣原理とは

鳩の巣原理とは、マニアックですが有名です。「部屋割り論法」とか言われることもあります。

巣が4つ、鳩が5羽いるとします。

そうすると、同じ巣に入る鳩が存在します。

別の言い回しにすると、「2羽以上の鳩が入る巣が存在する」

鳩の巣原理は、存在することの証明に使います。

例題：鳩の巣原理で存在を証明する

7個の整数がある時、その中には6で割った時の余りが等しい2個の整数のくみが存在することを示せ。

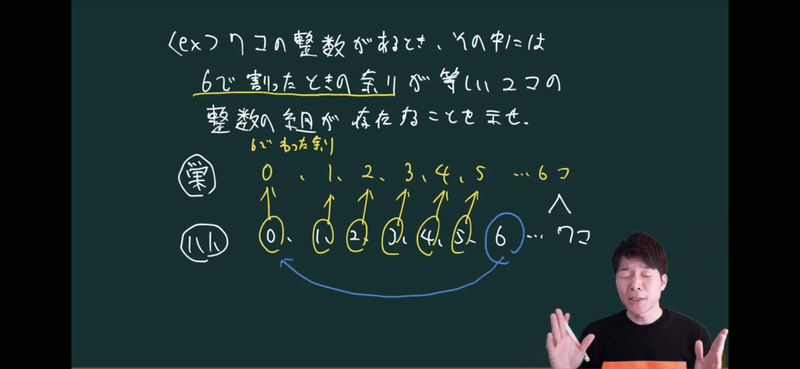
巣と鳩を決めてあげましょう。
巣：6で割った時の余り＝6個あります。
鳩：7個の整数とします。

答案
整数を6で割ったあまりは0,1,2,3,4,5のいずれかである。
この6個の数字を部屋に対応させる。
ここで7個の整数を6個の部屋に分けていくと
鳩の巣原理より、2個以上の整数が入る部屋が少なくとも1つ存在する。

問題１：入試問題です！！

相異なる4つの整数a,b,c,dからうまく2数を選べば、その差が3の倍数にできることを証明せよ。

巣：3で割ったあまり
鳩：4つの整数

少なくとも1つは同じ余りのものが存在する。
それを A,Bとして式を作る。（あまりが等しい）

以上よりその差は3の倍数である。

問題２

互いに異なる5個の格子点を任意に選ぶと、その中に次の性質を持つ格子点が少なくとも一対は存在することを示せ。
「一対の格子点を結ぶ線分の中点がまた格子点になる。」

上記のように選ぶと、中点はちょうど整数の点になります。

ダメなケース。上記にある青い二つの点は、中点が格子点（整数）にならないからダメ。

でも5つ選ぶと、「一対の格子点を結ぶ線分の中点がまた格子点になる。」というものが存在するのです。それを示していきます。

2個の格子点を座標(a,b)(c,d)え表す。
中点はそれを足して2で割ったもの。
それが整数になれば良い。

a+bもc＋dが偶数になればその中点は整数（格子点）になれます。

巣：座標を偶数と奇数の組み合わせで表すと、4つになる。
鳩：5個の格子点

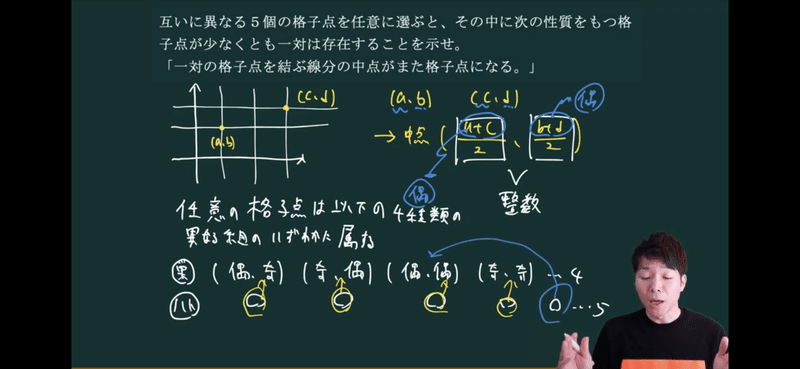
2点は必ずどこか同じ巣に入ります。
座標の奇偶が一致します。
奇数＋奇数＝偶数
偶数＋偶数＝偶数となります。

よって5つの異なる格子点は少なくとも2点は同じ組になり、それらのx座標同士、y座標同士の奇遇は一致する。よって中点の両座標は整数となる。

問題３

すべての桁が1である自然数111...111(1がa個並ぶ)と111...111(1がb個並ぶ。ただし、a>b)を29で割った余りが等しいとき、111...111(1がa-b個並ぶ)は29で割り切れることを示せ。

2種類の自然数をAとBとおく。
29で割ったあまりが等しいので上記のような式になる。

1がa-b個である自然数をCとおく。

A-Bは上記のようになる。
1がa-b個で、0がb個の自然数となる。

それをCを用いて表す。

整数＝分数の形になリました。

以上よりCは29で割り切れる。

問題４

すべての桁が1である自然数1,11,111,...,111...111(1が30個並ぶ)の中には29で割り切れるのもが存在することを示せ。

巣：29で割った時の余り＝29個
鳩：1が並んでいる自然数が30個

少なくとも1つは余りが同じものが存在する。
その2数をA,Bとする。
上記（青字）よりA-Bは29で割り切れる。

式変形をして整数＝分数の形に持っていく。

以上より、1がa-b個ある自然数は29で割り切れることが示されました。

鳩の巣原理はやっとかないと解けない問題です。
やっておくと解けるようになるのです！！

YouTube動画あります↓↓

整数の再生リストあります↓↓

整数が面白いほどわかる

⭐️数学専門塾MET【反転授業が日本の教育を変える】

⭐️獣医専門予備校VET【獣医学部合格実績日本一！！】