
たった1記事なのに訪問者爆増の謎…極限的必要十分条件のおかげか?
あけましておめでとうございます。今年度もよろしくお願いします。去年、僕はこちらの記事を書いた。
僕の中では予想外の展開だった。訪問者も1日あたり18人と、noteでは久々に見た数字だった(笑)。
記事で論理の応用例として「誰がこの記事を読んでいるの?」を記した。記事を書き終えた翌日、僕は書いた記事を印刷しながら読み直していた。
「これを書いていた自分よ、よくここが思いついたな」がある。
数学が好きである
数学に興味がある
昔、数学を勉強していた
数学は社会に出て役に立たないと思っている
数学が社会に出て役に立っている
役に立っているが、どう役に立つか、うまく説明できない
あなたはないだろうか?
気合入れて書いた記事なのに、思った以上に読まれなくてショックを感じた経験が。どうしたら読者も次々現れつつ、高評価で読んでくれるのだろう?
前回の記事を通し、僕は一つの答えが見えた。
本題へ入る前に、まず必要事項がある。
必要条件と十分条件

必要な基礎知識がある。大学共通テスト1問目で出てくる必要条件と十分条件だ。
前提条件がある下で、ある条件pとqに対し、
p→qが成り立つ場合(真)、pはqであるための十分条件。
q→pが成り立つ場合、qはpであるための必要条件だ。
「右に十分、左に必要」暗記すればいい。図だとpが狭いうえ、qの中に入っている。今から条件pとqを文章に置き換えてみよう。
実数x,yにおいて……p:x=y=1ならばq:xy=1である。
q:xyの値が1という情報(xとy、それぞれの値がわからない)に対し、p:x,yの値が1とはっきり定まっている。
pは具体的だ。qは一般的、抽象的、総合的と言える。
p→qこと十分条件を見ていく。確かにどちらも1なので、xyも1となり、正しい。一方q→pの場合、xy=1になるxとyはx=y=1だけでなく、共に-1もある。あるいはxに2、yに1/2(=0.5)でも達成できる。
x=y=1以外にも値がある(反例)。なので必要条件でない。
上図を見てほしい。pはqの中に入っていれば、とりあえず十分だ。
一方pの外にも値があると「qを満たす値はp以外(r)にもある=必要とはいえない」となってしまう。
別の表現で例えるなら、ご飯を食べるのにお箸で十分だが、お箸以外を使っても食べれる。例えばカレーライスだとスプーンを使って食べる。なので必要ではない。
どうすれば必要条件を満たせるか?
反例を省く条件を創ればいい。
先ほどの反例はxとyがともに-1の時、あるいは2と1/2の時、反例に入った。実数は整数、自然数、負の数、有理数に無理数など、虚数以外ならいろいろ含まれる。
一方自然数(0より大きい整数、少数や分数などでない)あるいは正の整数だと-1は含まれない。もちろん少数や分数も含まれない。
前提条件:自然数x,yにおいて……p:x=y=1ならばq:xy=1である。
qを満たす条件がpのみの場合、必要十分条件となる。
pだけが必要なのに、それ以外が入っちゃ必要条件でなくなる。

なおpとqが反対になると「必要条件だが十分条件でない」になる。
僕としてはpには限定的あるいは詳しい値や文章を、qには大雑把な文章や値を入れておくといいと思うんだ。
必要条件および十分条件はプログラミングでもメチャクチャ使う。
例えばunityにて階段を上る処理を行う時、対象物から短い線(Physics-Linecast)を飛ばし、短い線と地面が降れていれば真(True)、接していなければ偽(False)となる。
短い線を二つ用意する。一つは地面と接するよう垂直に。もう一つは地面と平行に。一つ目をgrounde、もう一つをstairというbool(真偽地判断)変数を置こう。
階段を登るための必要十分条件はgroundeかつstairを同時に満たしたときのみだ。
if(grounde && stair)階段上る処理
//unityことC#言語にて「かつ∩(キャップ)」は&&と記述
//英語だとandどちらか一方だと階段を登れない。
※一応最後に階段を上るプログラムを記載。ただしunityを使っている人にしか参考にならないと思う。
基本がわかったところで本題に入る。
反例つぶしは奥が深い
気合入れて書いた記事なのに、思った以上に読まれなくてショックを感じた……。
数学の論理を用いると、
p:気合を入れて書いた記事
q:思った以上に読まれる
ところが現実はq→pこと必要条件において反例が出てしまった。自分も意図しない・わからない反例だ。
どうしたらいいか。反例を潰す条件を創ればいいだけだ。
簡単な対策だからこそ、めちゃくちゃ頭を使う。
その条件、本当にそれでいいの?
気合を入れて書いた記事、誰に向けて読んでほしいのか?
誰でも構わないのか?
条件pに対する疑い+条件変更はもちろん、qにも疑いを持たねばならぬ。
読んでもらうだけでいいのか? とりあえず個別記事リンクを押せばいいのか?
いいねを押してもらいたいのか? 有料記事を購入してほしいのか?
そこからライン登録、メルマガ登録まで持ち込みたいのか?
目的によってpとqの条件ががらりと変わる。
未来を見つける「宝の条件」
条件を今一度見直した後、新しい条件を基に十分条件と必要条件を指摘していく。ただ掘り下げてはならない。目的は宝(超重要な言葉)の掘り出しにある。宝の正体が前回の記事にあった。
数学が好きである
数学に興味がある
昔、数学を勉強していた
数学は社会に出て役に立たないと思っている
数学が社会に出て役に立っている
役に立っているが、どう役に立つか、うまく説明できない
今あなたが読んでるこの記事、この時点ではまだ掘り下げていない。今から掘り下げるため、チラシの裏にとことん書く。
あなたも自分の記事を一つ用意して、やってみよう。まず決めねばならぬ条件はqだ。qは自分が求める展開でいい。
q:この記事を食い込むように読む
次はpを考える。pは一つ、二つ、三つと思いつく限りあげる。
上にある諸条件はすべてpこと十分条件が成り立つ場合だ。
ここで大きな問題がある。どれだけ十分条件が成り立とうとも、必要条件は一向に達成されない。必ず反例が生じる。
反例を一つずつあげて潰すと、限りなく必要十分条件ができる。すなわち……
極限必要十分条件
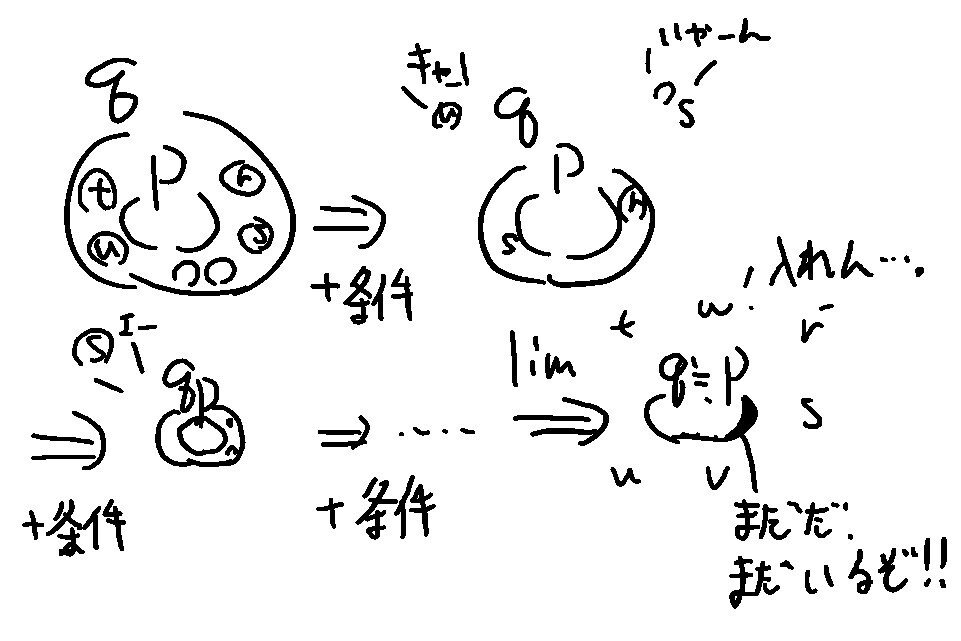
完全必要十分条件でなく、極限必要十分条件というべきか。
図で言うとqを絞って余分な条件(反例)を追い出し、q=pに近づける感じだ。
※極限的とは限りなくある値に近づけるのであって、完全一致ではない。例えば0.9999999999999999……は1に近づくが、1とは完全に一致しない。大きな目でみたら「1と同じ」に見えるだけ。
極限必要十分条件をやった結果が宝の条件にある。
単純に「これなら来る、これでも来る」浮かぶ内容から、そう簡単に浮かんでこない内容をとことん自問していく。
体を使わないという意味では楽だが、頭を使うという意味でメチャクチャきつい。きつい作業は何をもたらすのか?
今から一つの問いに答えてもらおう。
なぜ今、あなたはここまで読んでいるのか?
「答えてくれよ」言われたら、言葉に詰まるだろう。あなたの中にある感性(言葉で表現できない)が「ここを読め」導いた。
僕がきちんと極限必要十分条件をやって、あなたの感性が求める情報に答えた。あなたがここにいる。
もしあなたがここにいないとなると、僕は極限必要十分条件を怠った。あるいはやってはいるものの、反例を捨てないままやった結果と言える。
さらには世間の関心でないテーマを使って掘り下げた。多くの人が関心を持ってる分野だからこそ「私の悩み・疑問を満たしてくれる情報・答えはない」のだ。
極限必要十分条件は、あなたが漠然と求めている情報、うまく言語化できない悩みをはっきり言語化し「これじゃないか、私が求めているものは」にたどり着くための十分条件だ。
極限必要十分条件をただき出すには、簡単な数学(論理分野)の知識があればいい。ビジネス書では「ターゲット設定、ペルソナ設定」など言葉があるだろう。
ターゲット設定、僕はきちんとやっていた……が、極限必要十分条件を通して「大した掘り下げてなかったな」気づかされた。
極限必要十分条件が各方面に与える影響とは
僕が記事を書いているとき、極限必要十分条件をやるかやらないかで、記事の展開が大きく変わる。
極限条件をやると、文章に迷いがなくなる。どういう展開であなたに伝えたらいいかも浮かんでくる。僕の頭の中で勝手に数式が働き、計算通りに文章を書いている。
ただし頭の中では数式などを使っているのであって、実際に自分が数式を使っているのでない。数式計算を使わない数学だ。
反対に極限必要十分条件をやってないと「どこで終わらせようか」わからないまま、ぐだぐだが続く。書いている自分からすると、いい内容を書いているんだけど、読み手及び未来の自分からすると「なんだこれ」でしかない。
くわえて極限必要十分条件をこなすと、その後の戦略(自分たちが取るべき考え・行動など)にも影響を与える。迷いが生じるときは自分の中で「どれを最優先するか」が決まってないときだ。
実例:今あなたが読んでいる記事
現在あなたが読んでいる記事、記事投稿から7日前に書いたが、3日間書いては消してを繰り返した。記事一つにここまでやらなくていいんだけど、身近な習慣はやがてすべての生活習慣につながるから、さぼらずにやっている。
最初、記事タイトルは「潜在数学2:絶望を与えた事実」だった。何も考えないでそのままやっているだけだ。楽して成果を得たいわけだ。
記事タイトルに必要十分条件を入れよう。
q:潜在数学2:絶望を与えた事実
今からpを入れていく。
p:読者が~~な時、q:潜在数学2を必ず読む
前回の記事より「数学が役に立っているとわかっているが、どう説明したらいいかわからない」ときと置こう。
十分条件がとりあえず成立と仮定し、次はひっくり返す。
記事タイトル「q:潜在数学2:絶望を与えた事実」なら、p:数学が役に立っているとわかっているが、どう説明したらいいかわからない人は、必ず読む
あなたなら、この時必ず僕の記事を読むだろうか?
必ずでなければ高い確率でもいい。読むだろうか?
「読まない」選んだ時、何で読まないと思ったのか。
読まない理由こそ反例であり、潰さねばならぬ。
僕も「読まない」置いた。絶望を与えた事実は気になるけど、数学が役に立つかどうか、うまく説明できないのに、それを満たしてくれそうになさそう…。
pの条件だと「数学がいかに身近な生活で使っているか、役に立っているか、わかりやすく言語化してくれる情報」を求めてるわけだ。
なので同じ展開は当てはまらないとなる。
ここからが検討の始まりだ。考えがつかないと、さぼりたくなる。さぼってもいいんだ。己に「何が何でもやれ」命令してないから。
宝の言葉を探しながら「反例」を見つけ、反例を潰した内容を条件に加えていく。たとえば「読む時間がない」なら「読む時間がある」否定すればいいわけだ。
そもそもこの記事はいったい、何を伝えたいのか?
qを改めて見直さなければならない。
そこでタイトルを「極限的必要十分条件」に改めた。
極限的必要十分条件を知って、何を得るのか?
誰でもない「あなた」を引き込むための道具にした。
改めてq:極限的必要十分条件を使って、あなたを招き寄せる(仮題)が浮かんだ。後は再びpこと十分条件を創っていく。
※^:「かつ」を示す
数学に興味がある^
役に立つと分かっているが、うまく説明できない^
極限的必要十分条件という言葉に疑問を抱く^
学んだことを生かした仕事をしたい^
もう一度数学を学びなおしたい^
noteの訪問者を増やしたい
と、ここで「noteの訪問者を増やしたい」書いた。ここもまた「反例=別に増やさなくていい/増やし方を知ってるよ」を浮かべ、一つずつ検討しなければならない。
例えば「noteの訪問者を今よりも10倍ほど増やしたい^
増やし方を知らない or 増やし方を知っているが、興味ある」
今orを使った。orは「または」であり、どちらかを満たせばいいわけだ。もちろん両方でもいい。条件に当てはまらない言葉は「増やし方を知っている^他人の増やし方に興味ない」ときだけだ。
こうして絞り込んでいくと……
p:数学に興味ある^訪問者を一人でも多く一気に増やしたい^平日に読む時間がある^情報発信者として知名度を上げたいならば、
q:極限的必要十分条件で訪問者が爆増になったを読む。
これでもまだ反例は見つかるが、とりあえずここでしめる。これ以降の反例は起きてもいい(=それが理由で訪問者が減ってもいいと考えている)。
ここまで導き出すと、自分がどういう記事構成を練り、どうしていくか。誰に読んでもらいたいかも定まってくる。
やるもよし、やらぬもよし。
ここまで読んで、あなたに問われている事実は一つ。
「この記事があなたにとって面白くて、頭や体が動きたくなるか」どうかだ。面白そうと思ったら試してほしい。
今回の極限的必要十分条件を使ったのに、全く訪問者が来ない場合(未来の話)
noteに触れる人はもちろん、ネットに接する人が求めている情報を無視した。大きな市場に目をやらなかった「己の姿勢」に原因があると、はっきりわかる。
失敗は「この分野は大した求められてないんだな。ただ自分が語りたかっただけなんだな」がわかる。
極限的必要十分条件をやったからと言って、絶対来るわけでない。むしろ現時点の自分が見逃してた反例と向き合う瞬間でもある。
投稿翌日の報告
翌日午前11時時点で20人、いいねが3つもついていた。
これはこれで僕にとって悩みとうれしさをもたらした。
悩みは「数学と訪問者増、どちらに力を入れるべきか」迷いが生まれた。嬉しさは書かぬ。
悩み解決のために、あと数日経過観察が必要だ。
実験の一つとして、ぜひ堪能してもらいたい。
追記:階段上りプログラム
個々はプログラミングをやってる人、3Dゲームを作ってる人、参考にしてくれればありがたい。いくつか省略してるからわかりにくいと思う。
//先頭のpublic class は省略
private void Lines(){//地面とキャラの接触、床(layerWall)は例外
linePosS = transforms.position + groundS;//ベクトル
linePosE = transforms.position - groundE;
stairPos = linePosS + transforms.forward;
grounded = Physics.Linecast(linePosS, linePosE , layerGround );
stairs = Physics.Linecast(linePosS, stairPos , layerGround );
}//layerGroundとは private const int layerGround = 1<<3;
//3はレイヤー該当数番号が3にあるから。5なら1<<5private void Speeds(){ //動く動作
moving.x = moving2.x = axisH ; moving.z = moving2.z = axisV;//進道(moving)と向き(moving2)
moving.y = walkrun.y = rb.velocity.y; moving2.y = 0;
Rotats(); //武器構え以外は自由に回る
SetActions();StairActions(); //てつはうだけ移動不可
} private void SetActions(){ //普通に走る、歩く処理
if(!guardok){//ground,stairs関係ない
if(!sets) { //走る、歩く
if(runTrue){ //走る
if(axisV is 1 ) delays = 1;
if(axisH != 0) {delays = .8f;sideWalk = true;} else sideWalk = false;
if(axisV is -1 && !backon){delays = 0; backon = true; StartCoroutine(BackOff());}
} else { //上下のみ歩く
if(axisV != 0){delays = .4f;} if(axisH != 0) {delays = 0;}
} rb.velocity = wespdelay * speed * delays * velocitys;//左右は回転のみ
} else { //構え歩き
if(axisV is -1) delays = .1f;
else if(axisV is 1) delays =.3f;
if(axisH != 0) {delays = .2f;sideWalk = true;} else sideWalk = false;
rb.velocity = speed * delays * velocitys;
} //sets
} //ガード時は走るも歩くもできない,guard
}//rigidbodyの「位置」Y軸を固定private void Constraint(byte num){//キャラの動きを決める場合分け
switch (num) {
case 0: rb.constraints = RigidbodyConstraints.FreezeAll; break;//完全ストップ
case 1: rb.constraints = RigidbodyConstraints.None; rb.constraints = RigidbodyConstraints.FreezeRotationZ | RigidbodyConstraints.FreezeRotationX | RigidbodyConstraints.FreezePositionY; break;//普通に動く状態
case 2: rb.constraints = RigidbodyConstraints.None; rb.constraints = RigidbodyConstraints.FreezeRotationZ | RigidbodyConstraints.FreezeRotationX ; break;//落下,ジャンプ、階段上る
}
}好評なのか、誰も求めてないか、わからぬ。参考になれば。
追記2:極限必要十分条件
最初「極限的必要十分条件」書いていたが、的は形容詞となり、色々心残りがあったので、一部極限必要十分条件と書いた。
的には「~に関する」「~の性質を有する」など色々ある。
ないほうが、かえってすっきりする。
いいなと思ったら応援しよう!

