
流体力学 ジューコフスキー変換・翼(その1)
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
第49回目は,「ジューコフスキー変換・翼」について紹介していきますが,「等角写像」の続きです。よって,等角写像の理論編と例題編を基に進めますので,以前の記事もご覧ください。
約4ヶ月ぶりの投稿です。失踪しては,また気まぐれに再開していきますので,進捗はあまり期待せずでお願いします。
(1)ジューコフスキー変換とは
ジューコフスキーの変換については,等角写像の例題編で最後に少し触れましたが,あれはただの紹介でしたので,今回はもう少し掘り下げてみましょう。
そもそも,ジューコフスキーって人の名前でも「誰やねん」と思いますので,少し紹介します。
この法則を見つけた暇人こそ「ニコライ・ジューコフスキー」です。ロシアの物科学者,特に空気力学の研究業績が凄まじく,風洞の作成や航空力学の研究所設立など,現在の航空機はこの人なしでは到底成し得なかったことが容易に想像できます。
では,ジューコフスキー変換とは何なのでしょうか。
結論を述べると,「z平面上の流れをζ平面上に変換して,翼形周りの流れを検証するツール」です。これまでの記事で取り扱ってきたように,z平面からζ平面に変換をしてきましたので,図1にジューコフスキー変換によるz平面とζ平面の対応表を示します。
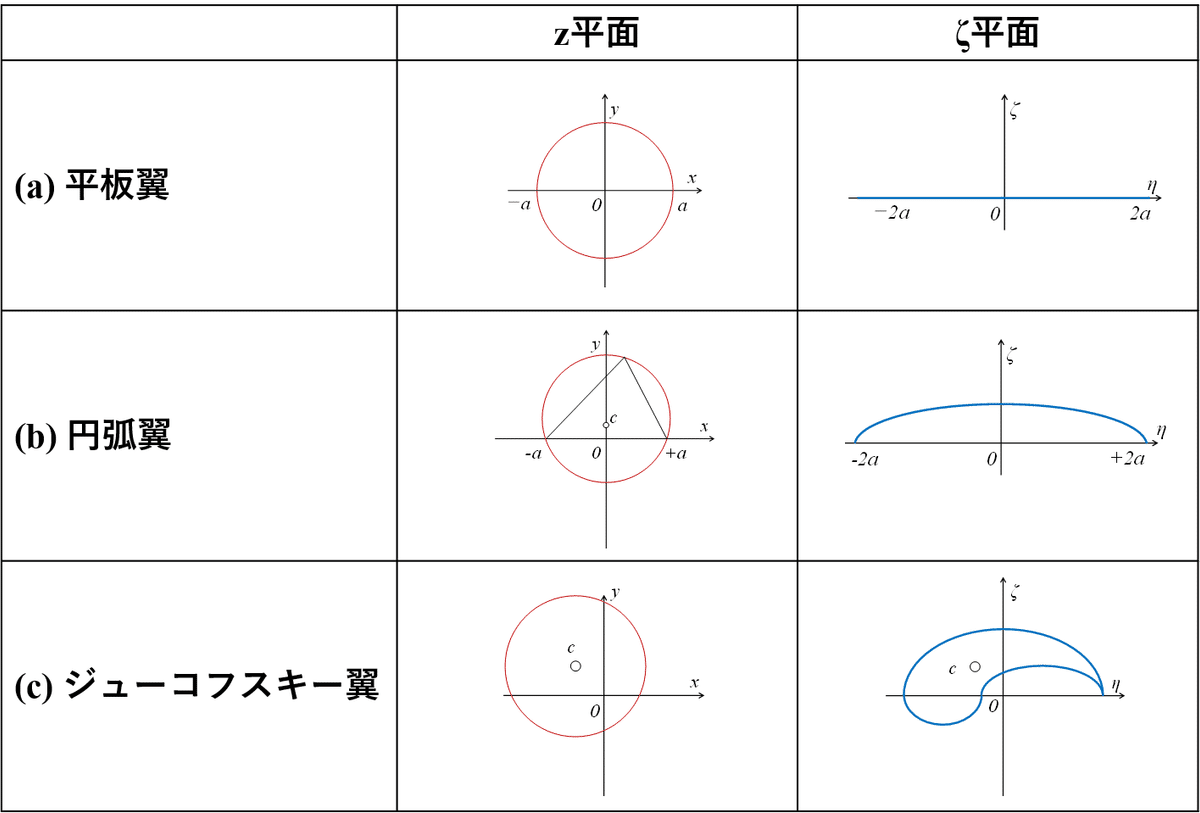
図1のようにz平面からζ平面に変換するときに使用するのが式(1)です。

この変換を使って色々やっていくと,最終的に翼形のような形状が出来たのです。それを「ジューコフスキー翼」と呼び,図1の最終段行のζ平面で現れる形状です。では,このような形状ができた理由を次項で掘り下げていきます。
(2)ジューコフスキー翼について
ジューコフスキー翼ができるまでの最初の条件について説明します。
ジューコフスキー翼ができる条件は「円柱に一様流れと2重湧き出しの流れが斜め向きに当たる状況」なので,このときの複素ポテンシャルを算出していくことで求められます。このときの円柱は,原点からx,y方向にそれぞれ僅かにズレているので,円の中心cと半径Rは式(2)で与えられます。

一様流れと2重湧き出しの流れ場における複素ポテンシャルを求めたい訳ですが,そのためには「一様流れと2重湧き出しの合成流れ」から始めていきます。過去の記事で紹介していますので,ご参考に。
まず,一様流れと2重湧き出しの合成流れの複素ポテンシャルは式(3)のように与えられ,そこに複素数zを代入していきます。

但し,斜め向きの一様流れを想定する場合は角度αの成分を含む複素数zでなければならないので,式変形を進めると式(4)のようになります。

式(4)で一様流れと2重湧き出しの合成流れから「一様流れと2重湧き出しの流れが斜め向きに当たる流れ」に変換できましたが,これで終わりではありません。
次に円の中心が原点からズレているので,これを考慮した複素数を更に加えて式変形すると,複素ポテンシャルは式(5)のようになります。

最後に,式(5)に半径Rを掛け,複素ポテンシャルに含まれている複素数zを全て変換すると,式(6)のようになります。つまり,式(6)まで到達できると速度ポテンシャルφと流れ関数ψの2つが分かることになって rとθの関数で表されることが分かります。

以上より,z平面での複素ポテンシャルの結果と円の中心がズレていることを踏まえて,2次元流れの極座標形式でx,y方向の式をそれぞれ考えると,式(7)のようになります。

よって,式(7)の結果を使ってζ平面の複素ポテンシャルを考えるとジューコフスキー変換の式(1)を上手く使って,式(8)のように変形できます。

ここまでの結果を総括すると,定数として定義できるのは中心から半径までの距離a,複素数c=a0+ib0,角度αの5つが任意に設定できるパラメータとなります。
次回は,このパラメータを設定して,z平面の流れとζ平面の流れをグラフ化してみましょう。
(3)まとめ
今回の記事のまとめを以下に示します。
①ジューコフスキー変換は,「z平面上の流れをζ平面上に変換して,翼形周
りの流れを検証するツール」である。
②ジューコフスキー翼は,z平面で「一様流れと2重湧き出しの流れが斜め向
きに当たる流れ場」をζ平面に変換したときにできる形状である。
以上です。最後まで閲覧頂きありがとうございました。
次回は,「ジューコフスキー変換・翼(その2)」について,解説する予定です。
サポートをして頂けると大変助かります。何かの支援ができるかもと思われた人をは何卒よろしくお願いします!
