流体力学　一様流れと2重わき出しの合成

　皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第２３回目は，第２２回目で予告した通り，「一様流れと2重わき出しの合成」について紹介していきます。

（１）一様流れと2重わき出しが合わさると…

　 では，「一様流れと2重わき出しの合成」について，解説してみます。図１に概略図を示します。図１を見ると，機械工学を専攻している方は，「これは…」と思う方もいるのではないかと思います。最終結果として得られる２次元流れは，あの「円柱回りの流れ」を示しているのです。

図１　一様流れと2重わき出しの合成の概略図

　意外と流体力学の講義でも，実験でもついて離れないのが「円柱回りの流れ」なのです。様々な理論構築をしていくときにこの「円柱回りの流れ」を起点に色々スタートするからだと筆者は考えています。それでは，数式を使って解き明かしていきましょう。

（２）一様流れと2重わき出しの合成の導出

　それでは，一様流れと2重わき出しの合成の導出をしていきます。まだ，「一様流れ」や「２重わき出し」のことについて知らない方や忘れてしまった方は以下の記事を確認してみて下さい。

　早速導出していきます。一様流れと2重わき出しの複素関数を重ね合わせができることを考慮すると，式（１）のように表せます（複素数z = x + iyと表せることを前提とします）。

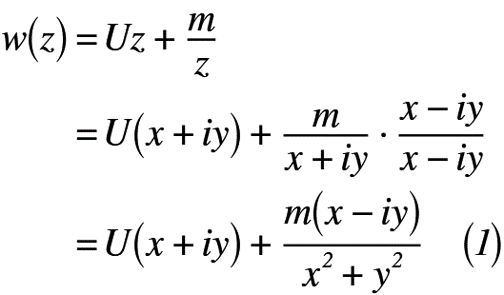
　但し，U：一様流れの速度，m：2重わき出しの強さとします。式（１）を使うことで，式（２）のように速度ポテンシャルφと流れ関数ψをそれぞれ表すことができます。

　ここで，式（２）で得られた流れ関数ψ=0の場合を考えると，円の方程式x^2+y^2=r^2であることを考慮したうえで，半径rを導出すると，式（３）のように表せます。

　式（３）は流れ関数ψ=0の場合を示していますが，このときの流線はx軸上の直線と原点からの半径rを示していることが分かります。つまり，この半径rから成立する流線を「円柱」（図面上では「円」ですが，奥手【スパン】方向の長さを１として考えているため，実際には「円柱」となります）と見なすことができ，一様流れと2重わき出しの合成によってできる2次元流れを「円柱回りの流れ」と呼ぶ習慣になっているようです。
　実は，この式（４）の流れ関数ψを使うことで，「一様流れと2重わき出しの合成グラフ」を描く準備はこの時点で終わっている状態です。これについては次回以降，紹介します。

（３）円柱回りの流れの速度分布

　ここでは，円柱回りの速度分布を算出してみましょう。式（３）で得られた結果を式（２）へ代入すると，式（４）のように表せます。

　式（４）に対して複素数zについて微分すると，複素共役速度が算出できるともに式（５）のように表せます。

　ここで，y軸上のx軸方向速度，もしくはx軸上のy軸方向速度を算出するためには，式（５）をx=0，もしくはy=0と置く必要があります。そのため，式（６），（７）のようにそれぞれ表すことができます。

　ここでまずは，yの値を変更したうえで，x軸上の速度分布を確認してみましょう。今回は，y=－5r～+5r（r刻み）としてグラフを描きます。そして，y=+r，+2rの場合を考えると，式（8-1），（8-2）のように表せます。

　それぞれ，yの値を変更したうえでグラフに描画すると，x軸上の速度分布は図２のように表せます。

図２　x軸上の速度分布

　次に，uの値を変更したうえでのy軸上の速度分布を確認してみましょう。今回は，u=0.01U～2U（0.01U刻み）としてグラフを描きます。そして，u=1.5U，2Uの場合を考えると，式（9-1），（9-2）のように表せます。

　それぞれ，速度uの値を変更したうえでグラフに描画すると，y軸上の速度分布は図３のように表せます。

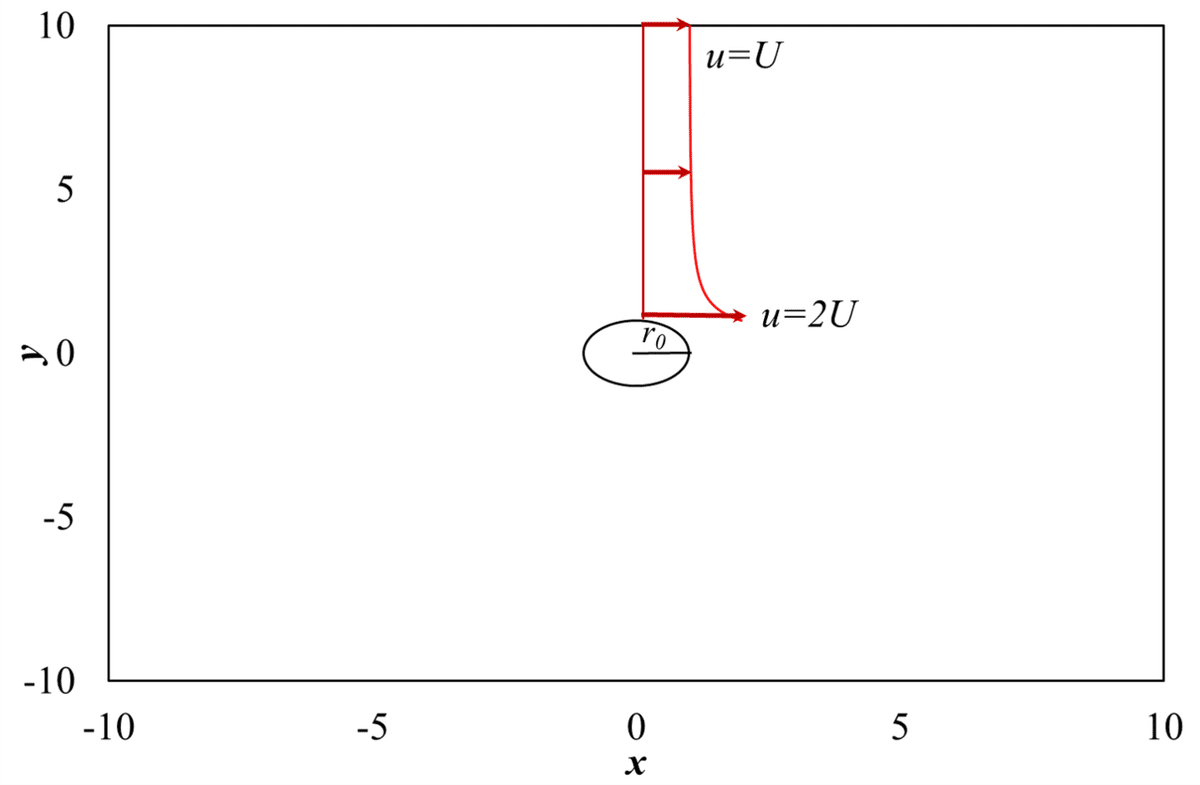
図３　y軸上の速度分布

　このように，円柱の近くはy軸上の速度が減速するのに対して，x軸上の速度は最大で2倍の速度になることが分かると思います。つまり，円柱の上端と下端が最大速度になることからやっかいな流体現象が起きます。
それが「剥離」です。細かい詳細は省きますが，途中から流れが円周に従わずに「剥離」が生じることで「カルマン渦」が発生することが過去の実験により分かっているのです。渦をはじめ，この「円柱回りの流れ」が流体現象の説明の起点になるのは，このような現象が起きるからだと筆者は考えています。

（４）y軸上の速度分布について

　前項では，円柱回りの速度分布を算出しましたが，y軸上の速度分布の別解を示してみましょう。共役複素速度の式（5）を用いて，円柱上のrではz=re^iθを代入すると，式（１０）のように表せます。

　ここで，極座標変換した速度分布を使って，式（１０）を代入すると，式（１１）のように表せます。もし，極座標変換した速度分布を知らない方は，以下の記事を確認してみて下さい。

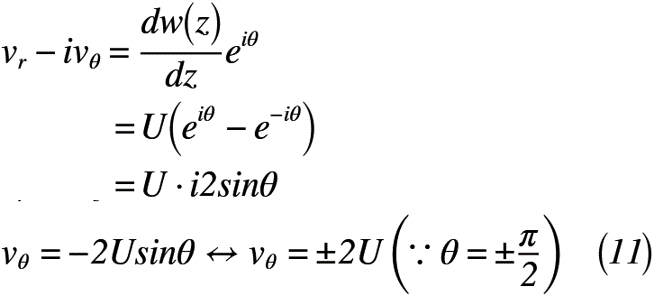
　よって，式（１１）に示すように，円周上の半径方向速度vr=0となるが，周方向速度vθ＝－2Usinθとなる。そして，θ=±π/2のときに，周方向速度が最大速度∓2Uとなり，式（9-2）及び図3で得られる結果と同様であることが分かるかと思います。

（５）まとめ

　今回の記事のまとめを以下に示します。
（１）一様流れと2重わき出しの合成で得られる２次元流れは，「円柱回りの流れ」である。
（２）円柱は，流れ関数ψ=0の場合に得られる半径rを使ったものである。
（３）y軸上の速度は，最大速度が一様流れの速度の2倍となる。

　以上です。最後まで閲覧頂きありがとうございました。

※次回は，一様流れと２重わき出しのグラフについて扱う予定です。