
流体力学 ブラジウスの公式(例題編)
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
今回は,第63回目として「ブラジウスの公式(例題編)」について紹介したいと思います。今回は,以前に投稿した「ブラジウスの第1公式」,「ブラジウスの第2公式」,「コーシーの積分定理」を使いますので,まだ知らない方はご確認ください。
(1)例題1
では,ブラジウスの第2公式を利用して翼の中心周りのモーメントMを求めてみましょう。以下に具体的な設問を示します。
流速u0の一様流れにおいて,平面翼(長さ4a)が迎え角αにて置かれた場合,翼の中心の周りのモーメントMは式(1)にて表されることをブラジウスの第2公式より導け。

はじめに,この状況を図示したものを図1に示します。図1は,x軸に適当な傾き角αをなす一様流れと循環を加えたz平面とジューコフスキー変換後のζ平面(平板翼:長さ4a)であり,過去の記事で取り扱った「翼理論(その4)」からの抜粋です。

今回は,翼の中心周りのモーメントMを求めるためにブラジウスの第2公式を使います。ブラジウスの第2公式を式(2)に示します。

ここで,図1に示したようにz平面からζ平面に変換するには,ジューコフスキー変換(式(3))が必要になります。
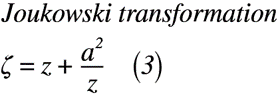
式(3)を式(2)に代入すると,式(4)のようになります。但し,ブラジウスの第2公式(式(2))を見るとz平面で議論が進むため,ζ平面に座標変換する必要があります。そのため,合成微分(チェーンルール)を使用することで,式(4)はz平面からζ平面に変換されたものになります。
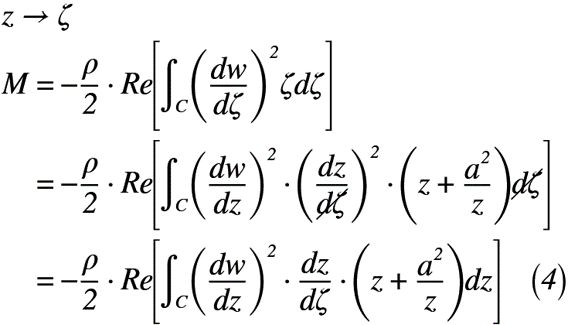
次に,x軸に適当な傾き角αを持たせたことでz’平面として考えているため,任意の角度αを持った複素数z’→zに変換した円柱周りの複素ポテンシャルw(z)は,式(5)のようになります。

得られた式(5)をzについて微分した複素速度dw/dzを式(6)に示します。但し,ブラジウスの第2公式に代入する形式に合わせるため,式(6)を2乗した形で示します。

ここで,さらにブラジウスの第2公式へ代入する形式に合わせるため,ジューコフスキー変換(式(3))からzについて微分したものを式(7)に示します。

ここで,式(7)を式(4)の下線部に代入すると,以下のようになります。ここで,注意するべきは(1-a^2/z^2)です。分母に(1-a^2/z^2)がある状態では,その後の議論をするのに障害となるため,マクローリン展開(1次項のみ)を使用します。

この状態にできれば,式(6)と式(7)を代入して計算を進めると,式(8)のようになります。

式(8)の状態でブラジウスの第2公式の積分をすることは不可能なので,チート技である「コーシーの積分定理」(式(9))を使用します。

式(9)を式(8)に適用すると,簡潔な形に持ち込むことができるので,式(10)のような複素数形式になります。

式(10)を式(4)へ代入すると,翼の中心の周りのモーメントMである式(11)が求められ,式(1)と同じになります。

よって,ブラジウスの第2公式を利用して翼の中心の周りのモーメントMを導出できたことになります。
(2)例題2
次に,ブラジウスの第1公式を利用して揚力Lを求めてみましょう。。以下に具体的な設問を示します。
流速u0の一様流れにおいて,平面翼(長さ4a)が迎え角αにて置かれた場合,揚力Lは式(12)にて表されることをブラジウスの第1公式より導け。

先ほど触れた「例題1」と同じ手順で進めます。基本的な進め方は以下の通りです。
複素ポテンシャル→複素速度→マクローリン展開→コーシーの積分定理
→ブラジウスの第1公式
「例題2」の状況も図1と同様のため,省略します。
では,ブラジウスの第1公式を式(13)に示します。「例題1」と同様に,z平面→ζ平面に座標変換した形式にしてあります。そのため,ζ平面におけるx,y方向の圧力をそれぞれPξ,Pηとします。

次に,x軸に適当な傾き角αを持たせたことでz’平面として考えているため,任意の角度αを持った複素数z’→zに変換した円柱周りの複素ポテンシャルw(z)は,式(14)のようになります。

得られた式(14)をzについて微分した複素速度dw/dzを式(15)に示します。但し,ブラジウスの第1公式に代入する形式に合わせるため,式(15)を2乗した形で示します。

ここで,さらにブラジウスの第1公式へ代入する形式に合わせるため,ジューコフスキー変換(式(3))からzについて微分したものを式(16)に示します。

ここで,式(16)を式(15)に代入すると,以下のようになります。ここで,注意するべきは(1-a^2/z^2)です。分母に(1-a^2/z^2)がある状態では,その後の議論をするのに障害となるため,マクローリン展開(1次項のみ)を使用します。

この状態にできれば,式(15)と式(16)を代入して計算を進めると,式(17)のようになります。

式(17)の状態でブラジウスの第1公式の積分をすることは不可能なので,チート技である「コーシーの積分定理」(式(18))を使用します。

式(18)を式(13)に適用すると,簡潔な形に持ち込むことができるので,式(19)のような複素数形式になり,ζ平面におけるx,y方向の圧力Pξ,Pηを求められます。

ここで求められた圧力の合力はρΓu0であり,一様流れの速度u0に対して垂直に働く力,すなわち揚力Lとして考えることができます。この考えに沿って行くと,式(20)のようになり,式(12)と同じになります。
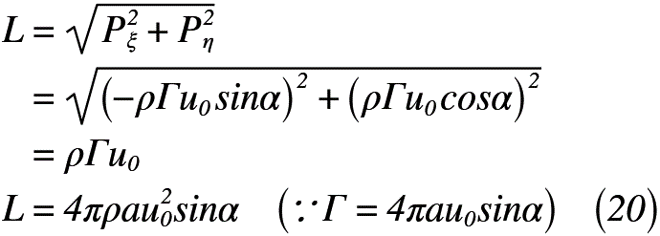
よって,ブラジウスの第1公式を利用して揚力Lを導出できたことになります。ちなみに式(20)の導出時に使用した循環Γの値については,過去の記事で紹介しているため,既に分かっているものとして取り上げています。(「翼理論(その4)」,(2)z平面のx軸に適当な傾き角αをなす一様流れと循環を加えた場合の循環より参照)
(3)まとめ
今回の記事のまとめを以下に示します。
① 流速u0の一様流れにおいて,平面翼(長さ4a)が迎え角αにて置かれた場合,ブラジウスの第1公式とブラジウスの第2公式により,揚力Lと翼の中心周りのモーメントMを導出することが可能である。
以上です。最後まで閲覧頂きありがとうございました。
次回は,「有限翼」について取り上げます。
サポートをして頂けると大変助かります。何かの支援ができるかもと思われた人をは何卒よろしくお願いします!
