
補足編 コーシーの積分定理
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
今回は,次回以降に投稿予定の「ブラジウスの第1公式」,「ブラジウスの第2公式」の解説で使用する「コーシーの積分定理」について取り上げてみようと思います。
(1)コーシーの積分定理とは
今回は,コーシーの積分定理を紹介していきます。この定理は,別名「コーシーの第1定理」とも呼ばれることがあり,この定理を導き出した暇人こそ,オーギュスタン=ルイ・コーシー(Augustin Louis Cauchy, 1789~1857)というフランスの数学者です。コーシーは,数学者として特に現在では「解析学」と呼ばれる学問で多大な功績を残した人であり,過去に記事で取り上げた「コーシー・リーマンの微分方程式」も彼の功績の1つです。その他,知っている人であれば,「コーシーの〇〇」のような公式や定理が出てくるほど,彼の功績は大きなものです。

(参考:Wikipediaフリー百科事典)
さて,コーシーの積分定理は端的にいうと,とある閉曲線上の複素関数w(z)が正則,かつ連続な導関数であるときの1周線積分が必ず「ゼロ」になるという定理です。正式に以下のような言い方をします。
「単純閉曲線(始点と終点以外に交点を持たない閉曲線)Cで囲まれた内部領域Dと置くと,複素関数w(z)が単純閉曲線Cかつ内部領域Dで正則,かつ連続な導関数のとき,式(1)が成立する。」

では,式(1)が成立するかどうかを証明してみましょう。単純閉曲線Cとその内部領域Dで正則な複素関数w(z)=φ+iψと複素数z=x+iyと置くと,複素関数w(z)の単純閉曲線Cに沿った1周線積分は,式(2)のように表されます。

ここで,以前の記事で紹介した「ストークスの定理」を使います。
但し,使用するにあたって注意があります。ストークスの定理は,微小な面要素の総和が外周Cの周積分に等しいことを証明したものです。ここで,微小な面要素の総和をそのまま使用すると都合が良くないので,微小な面要素の総和から単純閉曲線Cの面積素の総和に変更します。
これを「平面のグリーンの定理」といい,ストークスの定理の特殊な場合として使うことが出来ます。よって,ストークスの定理の特殊な場合である「平面のグリーンの定理」は式(3)のように表されます。

では,式(3)を式(2)に代入すると,式(4)が得られます。
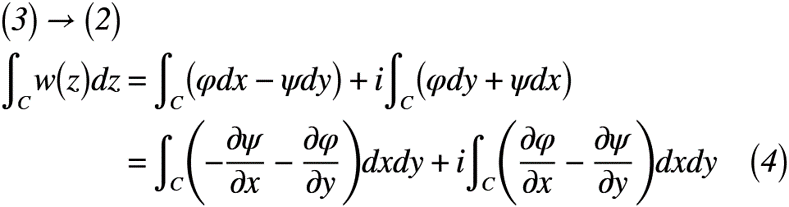
式(4)を更に式変形するには,コーシーの積分定理の文言で大事な言葉に注目します。「正則」です。複素関数が正則であれば,以前の記事で取り上げたコーシー・リーマンの微分方程式(以下,C-R方程式)が使えます。
そこで,式(5)にC-R方程式を示します。

式(5)を式(4)代入すると,式(6)のように表されます。

この式(6)は,式(1)と同じ式,すなわちコーシーの積分定理が証明できたことになります。コーシーの積分定理は,多くのパターンでも成立することが分かっていますので,次項ではそのパターンに注目してみましょう。
(2)積分路変形の原理
ここでは,コーシーの積分定理が成立するパターンの1つ目を見ていきましょう。図1に2点a,bを両端とする2つの曲線C1,C2がある場合の図形を示します。

コーシーの積分定理(式(1),または式(6))が成立することを前提に考えたうえで,図1の積分経路を数式化すると,式(7)のように表されます。今回は,a→bまでの経路を「プラス」として考えて,逆にb→aまでの経路を「マイナス」として考えることにします。

式(7)は経路によって,符合が変わることを用いて,始点と終点が同じであれば,経路が異なっていても(積分路変形),コーシーの積分定理が成立することを意味しています。これを「積分路変形の原理」と呼ぶこともあります。数式だけ見ると,線形性(加減法を使っただけ)が利用可能であることを述べただけですが,とても重要なのです。
(3)2重連結領域
コーシーの積分定理が成立するパターンの2つ目を見ていきましょう。図2に閉曲線C1の外部に他の閉曲線C2があり,複素関数w(z)は閉曲線C1,C2の上およびその間で正則である場合の図形を示します。(C2>C1)
図2のような状態を「2重連結領域」と呼びます。

およびその間で正則である場合(2重連結領域)
ここで,コーシーの積分定理が成立することを前提に考えたうえで,図2の積分経路を数式化すると,式(8)のように表されます。今回は,図2に示した反時計周りを「プラス」として考えることにします。

式(8)より,始点と終点が同じであれば,コーシーの積分定理が成立する積分路変形の原理を用いると,式(9)のように書き換えが出来ます。

線分ABと線分A’B’に注目し,両者の辺の長さが同じでかつ極限まで線分AA'と線分BB’の間を省略できるまで短くすると,式(10)に示すように取扱いの都合が良くなります。

また,線分AA‘と線分BB’を省略できるまで短くすると,式(11)のように表され,式(10),(11)を式(9)に代入すると,式(12)のようになります。


式(12)は,閉曲線C1の外部に他の閉曲線C2が存在するとき(2重連結領域)でも,コーシーの積分定理の積分定理が成立することを意味しています。
(4)単一閉曲線内部に半径rとなる円Kを境界とする2重連結領域
コーシーの積分定理が成立するパターンの3つ目を見ていきましょう。図3に単一閉曲線Cの内部に半径rとなる円Kを境界とする2重連結領域の図形を示します。また,複素関数はw(z)=(z-z0)^nとします。(n:正負の整数)
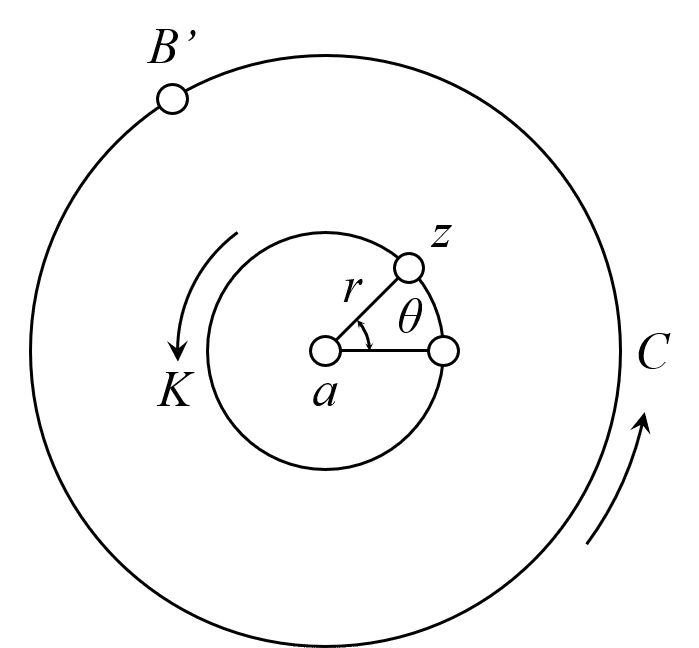
コーシーの積分定理(2重連結領域)を利用すると,式(13)のように表されます。

ここで,点aは原点からのズレ量と考えると,複素数z-a=re^iθ,複素数の微分dz = ire^iθdθとなるため,式(13)を書き換えると,式(14)のようになります。

式(14)を見ると,sinとcosで構成されているので,両者をそれぞれ0~2πの領域(円1周の領域)で積分すると,以下の式(15)のような結果が得られます。

式(15)を式(14)に代入すると,式(16)のようになります。

式(16)の結果から,n=-1の場合のみ複素関数w(z)=(z-z0)^nの積分値が「2πi」となり,n=-1以外の値の場合は複素関数w(z)=(z-z0)^nの積分値が全て「ゼロ」となるのです。
もし,点aは原点からのズレ量と考えずa=0の特別な場合であっても,複素関数w(z)=z^nの積分値は,n=-1の場合のみ「2πi」となり,n=-1以外の値の場合は,式(17)のように全て「ゼロ」となります。

よって,式(16),(17)の結果から,コーシーの積分定理は,n=-1の場合のみ積分値を持つことになり,n=-1以外の値の場合は全て「ゼロ」となります。
(5)まとめ
今回の記事のまとめを以下に示します。
① コーシーの積分定理を導き出したオーギュスタン=ルイ・コーシーは,フランスの数学者であり,解析学で多大な功績を残した。
② コーシーの積分定理の導出には,ストークスの定理の特殊な場合である平面のグリーンの定理とコーシー・リーマンの微分方程式を用いる。
③ コーシーの積分定理は,積分路変形や2重連結領域でも成立するが,一閉曲線Cの内部に半径rとなる円Kを境界とする2重連結領域の場合のみ,特殊なパターンが存在する。
以上です。最後まで閲覧頂きありがとうございました。
※本記事は,「ブラジウスの第1公式」,「ブラジウスの第2公式」にて利用する背景知識となります。
サポートをして頂けると大変助かります。何かの支援ができるかもと思われた人をは何卒よろしくお願いします!
