補足編　ストークスの定理

　皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　今回は，物理数学でよく利用される「ストークスの定理」について，取り扱っていきたいと思います。本来なら「循環の証明」と同時投稿を目指しておりましたが，実現できず大変申し訳ございません。

（１）ストークスとは？

　ベクトル解析や流体力学，あるいは光学などでよく登場する「ストークス」先生ですが，これらの分野を一度は学んだ方にとっては，聞いたことがないという方はいないでしょう。ここでは，ベクトル解析で登場する「ストークスの定理」までの歴史を少し追っていきましょう。
　本名は，「ジョージ・ガブリエル・ストークス（George Gabriel Stokes）」といい，アイルランドの数学者，物理学者です。主な功績としては，粘性流体の基礎方程式であるナビエ＝ストークスの方程式（Navier–Stokes equations），流体中の落下する粒子速度を算出するストークスの式，ラマン効果（散乱）で発生するストークス散乱や今回取り上げるストークスの定理など様々な分野で多くの功績を残されている方です。
　しかし，このストークスの定理ですが，友人であるウィリアム・トムソン（William Thomson）から送られた手紙から定理を知ったそうです。驚くことに，最初の世に現れたのはケンブリッジ大学の数学の優等試験で「これを証明せよ」と出題されたそうです。私がもし優秀な学生であったとしても「ふざけんな！」とブチギレしているところでしょう。笑
　そんな逸話が残っている「ストークスの定理」ですが，ストークス自身が見つけたものではないことが分かって頂けたと思います。今回は，ストークスの定理の証明を取り扱っていきましょう。

※参考URL: https://www.kurims.kyoto-.ac.jp/~okamoto/paper/green/node5.html

（２）ストークスの定理について

　では，ストークスの定理を見ていきましょう。図1に示すようなベクトル場a = [a, b, c]の中に閉曲線Cで囲まれた曲面Sがあるとき，式（1）が成立します。この式（1）がストークスの定理の式を示します。

　但し，単位法線ベクトルnをSの正の側にとり，周回積分路Cは正の向きに回るものとします。
　式（1）を見てもイメージしづらいと思いますが，ストークスの定理が言いたいことは，「微小な面要素の総和が，外周Cの周積分に等しい」ことを述べています。これが分かると，今まで流体力学で解説して当たり前のように使っていた「渦度」や「循環」のモデル化および数式化ができるようになります。次に，ストークスの定理を証明してみましょう。

（３）ストークスの定理の証明

　それでは，式（１）を証明してみましょう。まずは，式（2）に示すように準備します。

　式（２）を式（１）へ代入すると，式（３）～式（５）のように表せます。

　ここで面積素ベクトルdS = ndSより式（６）のように表せます。

　曲面ＳがベクトルＰ=[x, y, z]の場合，その単位法線ベクトルnは，式（7）のように表せます。

　よって，式（７）を式（６）に代入すると，面積素ベクトルdSが式（８）のように表せます。

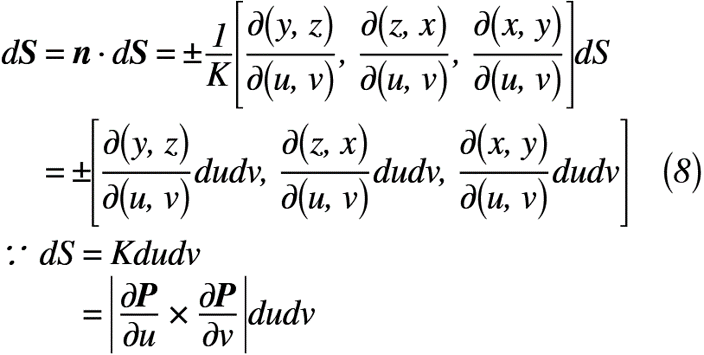
　式（６）と式（８）が等しいことを利用すると，式（９）～式（１１）のように表せます。

　式（９）～式（１１）までがいわゆるx, y, z方向のベクトル成分を示しています。したがって，どれか1方向の証明ができれば，残り2方向の証明が可能となり，3成分の証明が可能となります。
　今回は，ｘ方向に該当する式（９）を証明します。式（２）を式（９）へ代入して計算を進めると式（３）が証明出来ました。

　残りの２方向の証明についても，式（１０）→式（４），式（１１）→式（５）と同様に示すことが出来るため，式（１）に示すようなストークスの定理が証明できました。

（４）まとめ

　今回の記事のまとめを以下に示します。
（１）ストークスの定理と名付けられたストークスは，数多くの功績を残しているが，ストークス自身がストークスの定理を見つけた訳ではない。
（２）ストークスの定理は，最初に世の中に出たのはケンブリッジ大学の試験問題とされている。
（３）ストークスの定理は，微小な面要素の総和が，外周Cの周積分に等しいこと述べている。

　以上です。最後まで閲覧頂きありがとうございました。

※本記事は，「循環の証明」にて利用する背景知識となります。このほかにも使われるかと思いますが…。