流体力学　渦に関する法則（その4）

　皆様おはこんばんちは。そして，お疲れ様です。

 　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第３６回目は，前回の予告通り「渦に関する法則」について紹介していきます。

 

（１）渦の何を取り扱うのか？

 　 では，「渦に関する法則」について，解説していく訳ですが，筆者以外は，「何をそんなに取り上げる必要があるの？」と思うはずです。そこで，「渦に関する法則」として取り上げる内容を以下に箇条書きで示します。そして，各項目で記事にする予定ですので，興味のある分野や関連項目で見たいなどでいいかと思います。

（ⅰ）渦管を取巻く閉曲線Cで循環Γが成立するのか。
（ⅱ）2次元平面から3次元曲面でも循環Γが成立するのか。
（ⅲ）2次元流れの渦度は時間経過によってどう変化するのか。
（ⅳ）閉曲線Cに沿う循環Γは時間経過でどう変化するのか。

　基本的には，渦と取り扱うときに必ず登場する循環Γがどのようなモデルでも成立するのかをメインに取り扱います。今回は，「（ⅳ）閉曲線Cに沿う循環Γは時間経過でどう変化するのか。」について投稿していきます。今回が「渦に関する法則」の最終回となります。

 

 

（２）閉曲線Cに沿う循環Γは時間経過でどう変化するのか。

 

（２－１）数式による証明（準備編）

 　今回も， 数式による証明をメインに考えていきます。結論から言えば，「閉曲線Cに沿う循環Γは時間経過でどう変化するのか。」の「循環Γの時間経過」については，式（1）のようになればよいのです。

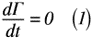
 　では，式（1）が何を示しているかというと，循環Γが時間経過に伴って，ゼロになることを指しているのです。要するに「渦度」がどの時間で見ても，ずっと「ゼロ」になるのです。前回の渦に関する法則（その3）で取り上げた「（ⅲ）2次元流れの渦度は時間経過によってどう変化するのか。」で渦度がゼロになることを紹介したので，この結果になることが想像できた方は素晴らしく勘の良い方だと思います。

 

　それでは，証明するために必要な数式は，2つ存在します。

　1つ目は，ナビエ・ストークスの方程式（以下，N-S方程式）です。流体力学の世界で，これが解けると，様々な流体現象を記述できるという（偏微分）方程式です。前回の記事でも紹介していますので，詳しい説明は省略します。

　2つ目は，ベルヌーイの定理です。特に水力学の分野で活躍する式です（土木工学では，水理学と呼ぶそうです）。密度が常に一定となる（温度変化により体積が変化しても質量が絶対変化しない理想的な状態となる）非圧縮性流体であることが前提であれば，流体の持つ圧力エネルギー，速度エネルギーおよびポテンシャルエネルギー（多くの場合は，位置エネルギーに該当する）の総和がどの位置にあってもエネルギー保存するというものです。つまり，どの位置をとっても，圧力や速度が変動してもトータルのエネルギーは適当な値から変わらないことを意味します。この性質を今回は利用します。

　次項では，実際に数式による証明をしていきます。

 

（２－２）数式による証明（実践編）

 　では，本格的に証明してみましょう。前回の記事と同様に，時間によって変化しない定常流れ，密度ρが変化しない非圧縮性流体を取り扱い，２次元流れとすることとします（よくわからない人は，とりあえず式を解くのを簡単にしているものと考えてください）。 

　まず，式（1）で登場する循環Γを展開すると，Γは各成分の速度（2次元流れの場合は，x, y方向の速度に分解できる）に分解して考えると，式（2）のように表せます。 

　ここで，x, y方向の速度u,vを一気に処理すると大変なので，個別に処理していきます。x方向の速度uを時間について微分すると，式（3）のように表せます。

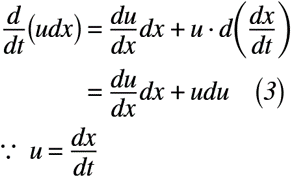
 　ここで，流体の運動の様子を数式で記述したN-S方程式に式（3）を代入すると，式（4）のように表せます。

　同様の処理をy方向の速度vについても行います。y方向の速度vを時間について微分し，N-S方程式に代入した結果は，式（5），（6）のように表せます。

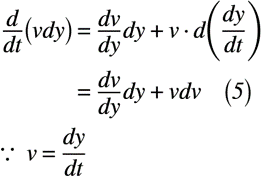
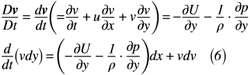
　ここまでに得られた式（4），式（６）の結果を式（2）に代入すると，式（7）のように表せます。

　最後に，式（7）を時間について積分すると，式（8）のように表せます。したがって，循環Γが時間経過に伴って，ゼロになることが証明できるため，式（9）のように表せます。

　式（8）で得られる結果こそ，ベルヌーイの定理と呼ばれる式と同一になります。そして，最初の仮定である「循環Γが時間経過に伴って，ゼロになる」式（1）を使うと，式（7）のようになります。

　また，数学的には定数（いわゆる，0，1/2，0.3，πなど）を積分すると，必ずゼロになるということが分かっているので，式（7）の右辺から式（8）の右辺にそのまま繋がっています。つまり，数学的にも間違っていないことになります。

　そして，式（7）から登場しているCは閉曲線を示しています。循環Γが閉曲線Ｃの内側に存在していれば，コーシー・リーマンの正則条件を満たしているので，どちらにしてもゼロになることは担保されていることになります。詳しくは，以前の記事を参考にしてみて下さい。

 流体力学　コーシー・リーマンの微分方程式｜素人が伝えてみる機械工学ブログ｜note

 

（３）まとめ

　今回の記事のまとめを以下に示します。
（１）渦に関する法則は，主に4つ取り上げる。今回は，（ⅳ）閉曲線Cに沿う循環Γは時間経過でどう変化するのか。
（２）2次元流れの循環は，時間経過とともに変化しないことを証明するには，N-S方程式およびベルヌーイの定理の2つを用いる必要がある。
（３）循環は，時間経過しても変化しないのはベルヌーイの定理が成立するためである。

 　以上です。最後まで閲覧頂きありがとうございました。

 

※次回は，「渦周りのポテンシャル流れ（その1）」を取り扱う予定です。

 

 

（4）おまけ

 　最近，noteが数式に対応し始めたような記事を拝見しました。これも数学や物理を解説する人が増えたことや数式をweb上にかきたいと希望する人が増えたからでしょうね。

note上で数式が表示できる機能を実験中です｜note公式｜note

　ですが，筆者はいわゆる「TeX記法」が「できない」人です。今まで，数式を書く機会があるときは，すべてMicrosoftの数式エディタ3.0を使って済ませていました（笑）。
　その他は，それに近いものを使ってしのいでいました。今も数式をあえて画像として記事を書いていますが，これを機会にTeX記法を覚えた方がいいのでしょうか…。

　筆者はかなりのめんどくさがりなので，自分に利益がないと腰が動かない人です。ここ最近の業務でもめったに使うことはないので，現在検討中です。もし，是非利用した方がいいという方は，何かしらの手段で間接的に教えて頂けると幸いです。