
高校数学をプログラミングで解く(数学B編)「2-5 座標空間における図形」
マガジンリスト > 数学B編 2.空間のベクトル > 2-5 座標空間における図形
はじめに
今回は、数学Bで学ぶ「座標空間における図形」について、線分の内分点や外分点の座標を計算して空間にプロットするプログラムや座標軸に垂直な平面を描くプログラム、そして球面を描くプログラムを作成します。
線分の内分点・外分点の座標
$${\mathrm{A}(x_1,y_1,z_1),\mathrm{B}(x_2,y_2,z_2),\mathrm{C}(x_3,y_3,z_3)}$$とします。
① 線分$${\mathrm{AB}}$$を$${m:n}$$に内分または外分する点の座標は、
$$
\mathrm{内分点} \left( \frac{nx_1+mx_2}{m+n},\frac{ny_1+my_2}{m+n},\frac{nz_1+mz_2}{m+n} \right)
$$
$$
\mathrm{外分点} \left( \frac{-nx_1+mx_2}{m-n},\frac{-ny_1+my_2}{m-n},\frac{-nz_1+mz_2}{m-n} \right)
$$
② △$${\mathrm{ABC}}$$の重心$${\mathrm{G}}$$の座標は
$$
\mathrm{G} \left( \frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3},\frac{z_1+z_2+z_3}{3} \right)
$$
座標軸に垂直な平面の方程式
点$${\mathrm{P}(a,b,c)}$$を通り、
① $${x}$$軸に垂直な平面($${yz}$$平面に平行な平面)の方程式は$${x=a}$$
② $${y}$$軸に垂直な平面($${zx}$$平面に平行な平面)の方程式は$${y=b}$$
③ $${z}$$軸に垂直な平面($${xy}$$平面に平行な平面)の方程式は$${z=c}$$
球面の方程式
中心が$${\mathrm{C}(a,b,c)}$$、半径が$${r}$$の球面の方程式は
$$
(x-a)^2+(y-b)^2+(z-c)^2=r^2
$$
一般形
$$
x^2+y^2+z^2+kx+ly+mz+n=0 (\mathrm{ただし、} k^2+l^2+m^2-4n>0)
$$
線分の内分点・外分点の座標に関する問題
まず、線分の内分点・外分点の座標に関する問題を解くプログラムを作成していきます。
線分の内分点・外分点の座標に関する問題
3点$${ \mathrm{A}(3,-3,-1) }$$、$${ \mathrm{B}(2,0,5) }$$、$${ \mathrm{C}(4,-1,5) }$$に対して、次の各点の座標を求めて、空間上にプロットせよ。
(1) 線分$${\mathrm{AB}}$$を$${3:5}$$に内分する点$${\mathrm{P}}$$
(2) 線分$${\mathrm{BC}}$$の中点$${\mathrm{Q}}$$
(3) 線分$${\mathrm{AB}}$$を$${1:3}$$に外分する点$${\mathrm{R}}$$
(4) △$${\mathrm{PQR}}$$の重心$${\mathrm{G}}$$
問題の考え方(空間座標の扱いについて)
Processingで空間座標$${\mathrm{P}(x,y,z)}$$を扱う場合、空間ベクトルや位置ベクトルを扱うときと同様に、PVectorクラスを利用すると便利です。そのため、例えば、$${\mathrm{P}(x,y,z)}$$は
PVector p = new PVector(x,y,z);としてベクトルのように扱うことにします。
線分の内分点・外分点の座標位置を求めてプロットするプログラム
今回の問題は線分の内分点・外分点の座標位置を定義通りに求めてプロットするようにプログラミングしていくだけですが、上記で説明したように、PVectorクラスを利用して計算を行います。
記事『高校数学をプログラミングで解く(数学B編)「2-0-3 右手系で図形を描く」』で作成したスケッチ「draw3DCoordinates_temp」を再利用します。以下の zip ファイルをダウンロードして展開または解凍してください。
そして、スケッチの名前(フォルダ名)を「plot3Dpoints」と変更し、またスケッチ「plot3Dpoints」内の「draw3DCoordinates_temp.pde」ファイルの名前を「plot3Dpoints.pde」に変更します。そして、pdeファイル「plot3Dpoints.pde」をダブルクリックしてスケッチ「plot3Dpoints」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「plot3Dpoints」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
// 内分点・外分点などを描く
float range; // 座標系での表示範囲-range≦x,y.z≦range
float res; // 座標系のサイズをキャンバスのサイズに変換するパラメータ
float angle = 0.0;
PVector a, b, c; // 点A,B,Cの空間座標
PVector p; // 線分ABを3:5に内分する点の空間座標
PVector q; // 線分BCの中点の空間座標
PVector r; // 線分ABを1:3に外分する点の空間座標
PVector g; // △PQRの重心の空間座標
void setup(){
size(400, 400, P3D);
noFill();
ortho();
range = 10.0;
res = width / 2.0 / range;
// 点A,B,Cの位置ベクトル
a = new PVector(3.0, -3.0, -1.0);
b = new PVector(2.0, 0.0, 5.0);
c = new PVector(4.0, -1.0, 5.0);
// 線分ABを3:5に内分する点の空間座標
float m = 3.0;
float n = 5.0;
p = a.copy().mult(n).add( b.copy().mult(m) ).mult(1.0/(m+n));
// 線分BCの中点の空間座標
m = 1.0;
n = 1.0;
q = b.copy().mult(n).add( c.copy().mult(m) ).mult(1.0/(m+n));
// 線分ABを1:3に外分する点の空間座標
m = 1.0;
n = 3.0;
r = a.copy().mult(-n).add( b.copy().mult(m) ).mult(1.0/(m-n));
// △PQRの重心の空間座標
g = p.copy().add( q.copy() ).add( r.copy() ).mult(1.0/3.0);
println("点Pの空間座標:", p);
println("点Qの空間座標:", q);
println("点Rの空間座標:", r);
println("点Gの空間座標:", g);
}
void draw(){
background(204); // 背景をグレーにする
// 視点を設定する
camera(200.0, -200.0, 100.0, 0.0, 0.0, 0.0, 0.0, 0.0, -1.0);
// マウスボタンが押されたときの処理
if(mousePressed){
if( mouseButton == LEFT ){ // 左ボタンがおされたときはz軸時計周りに回転
angle = angle + 1.0;
} else if( mouseButton == RIGHT ){ // 右ボタンがおされたときはz軸反時計周りに回転
angle = angle -1.0;
} else {
}
}
// z軸周りに回転
rotateZ(radians(angle));
// 座標軸の設定
strokeWeight(1);
fill(255,0,0);
stroke(255,0,0);
arrow3D(0.0,0.0,0.0,range * res,0.0,0.0); // x軸(赤色)
fill(0,255,0);
stroke(0,255,0);
arrow3D(0.0,0.0,0.0,0.0,range * res,0.0); // y軸(緑色)
fill(0,0,255);
stroke(0,0,255);
arrow3D(0.0,0.0,0.0,0.0,0.0,range * res); // z軸(青色)
noFill();
stroke(0,0,0);
// 以下に、図形を描いていく
// 点A,B,Cをプロットする(黒色)
strokeWeight(5);
// fill(0,0,0);
stroke(0,0,0);
point_rhs(a.copy().mult(res));
point_rhs(b.copy().mult(res));
point_rhs(c.copy().mult(res));
// △ABCを描く(黒色)
strokeWeight(1);
noFill();
triangle_rhs(a.copy().mult(res),b.copy().mult(res),c.copy().mult(res));
// 点Pをプロットする(黄色)
strokeWeight(5);
stroke(255,255,0);
point_rhs(p.copy().mult(res));
// 点Qをプロットする(水色)
stroke(0,255,255);
point_rhs(q.copy().mult(res));
// 点Rをプロットする(桃色)
stroke(255,0,255);
point_rhs(r.copy().mult(res));
// △PQRを描く(白色)
strokeWeight(1);
stroke(255,255,255);
triangle_rhs(p.copy().mult(res),q.copy().mult(res),r.copy().mult(res));
strokeWeight(5);
point_rhs(g.copy().mult(res));
}ソースコード1 線分の内分点・外分点を求めてプロットするプログラム
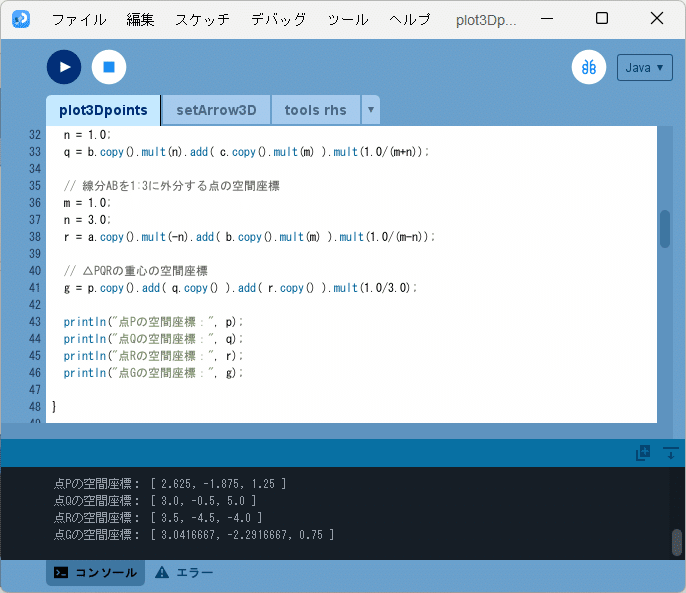
このスケッチ「plot3Dpoints」を実行すると、図1のように、開発環境ウィンドウのコンソールに、各点の座標位置が
点Pの空間座標: [ 2.625, -1.875, 1.25 ]
点Qの空間座標: [ 3.0, -0.5, 5.0 ]
点Rの空間座標: [ 3.5, -4.5, -4.0 ]
点Gの空間座標: [ 3.0416667, -2.2916667, 0.75 ]
と出力されます。
また、図2のように、実行ウィンドウのキャンバスに空間の座標系を表す3つの空間ベクトル(赤色:$${x}$$軸、緑色:$${y}$$軸、青色:$${z}$$軸)を基準にして、3点$${\mathrm{A,B,C}}$$とそれらの3点を頂点とする△$${\mathrm{ABC}}$$を黒色、点$${\mathrm{P}}$$を黄色、点$${\mathrm{Q}}$$を水色、点$${\mathrm{R}}$$を桃色、点$${\mathrm{G}}$$と△$${\mathrm{PQR}}$$を白色で表示しています。
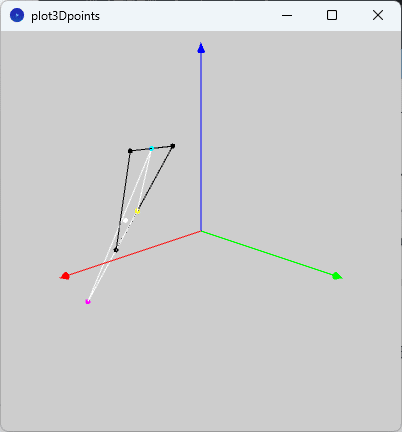
なお、実行ウィンドウのキャンバス内をクリックすると$${z}$$軸回りに図形が回転するので、いろいろな角度から空間ベクトルを眺めてみてください。
座標軸に垂直な平面の方程式に関する問題
次に、座標軸に垂直な平面の方程式に関する問題を解くプログラムを作成していきます。
座標軸に垂直な平面の方程式に関する問題
点$${\mathrm{A}(8,-2,4)}$$を通る、次のような平面の方程式を求め、空間上に描け。
(1) $${x}$$軸に垂直
(2) $${z}$$軸に垂直
(3) $${zx}$$平面に平行
座標軸に垂直な平面を描くプログラム
今回の問題は、座標軸に垂直な平面の方程式の定義通りであり、特に計算することもないので、直接平面を描いていきます。なお、平面は、記事『高校数学をプログラミングで解く(数学B編)「2-1 空間の座標」』の『プログラムの解説「平面の描画」』で解説したものと同じ方法で描いていきます。
先程作成したスケッチ「plot3Dpoints」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「drawPlanes」と変更し、またスケッチ「drawPlanes」内の「plot3Dpoints.pde」ファイルの名前を「drawPlanes.pde」に変更します。そして、pdeファイル「drawPlanes.pde」をダブルクリックしてスケッチ「drawPlanes」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「drawPlanes」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
// 平面を描く
float range; // 座標系での表示範囲-range≦x,y.z≦range
float res; // 座標系のサイズをキャンバスのサイズに変換するパラメータ
float angle = 0.0;
PVector a; // 空間の座標
void setup(){
size(400, 400, P3D);
noFill();
ortho();
range = 10.0;
res = width / 2.0 / range;
// 点Aの座標を表わすベクトル
a = new PVector(8.0, -2.0, 4.0);
}
void draw(){
background(204); // 背景をグレーにする
// 視点を設定する
camera(200.0, -200.0, 100.0, 0.0, 0.0, 0.0, 0.0, 0.0, -1.0);
// マウスボタンが押されたときの処理
if(mousePressed){
if( mouseButton == LEFT ){ // 左ボタンがおされたときはz軸時計周りに回転
angle = angle + 1.0;
} else if( mouseButton == RIGHT ){ // 右ボタンがおされたときはz軸反時計周りに回転
angle = angle -1.0;
} else {
}
}
// z軸周りに回転
rotateZ(radians(angle));
// 座標軸の設定
strokeWeight(1);
fill(255,0,0);
stroke(255,0,0);
arrow3D(0.0,0.0,0.0,range * res,0.0,0.0); // x軸(赤色)
fill(0,255,0);
stroke(0,255,0);
arrow3D(0.0,0.0,0.0,0.0,range * res,0.0); // y軸(緑色)
fill(0,0,255);
stroke(0,0,255);
arrow3D(0.0,0.0,0.0,0.0,0.0,range * res); // z軸(青色)
noFill();
stroke(0,0,0);
// 以下に、図形を描いていく
// 点Aをプロットする(黒色)
strokeWeight(5);
stroke(0,0,0);
point_rhs(a.copy().mult(res));
// 平面上の点を表す座標
PVector plane_point = new PVector(0.0,0.0,0.0);
// 平面を点群で表わすときの各軸方向に並べる点の数
int plot_num = 100;
// 図形を描く範囲
float m_range = -range;
float p_range = range;
// 点Aを通り、x軸に垂直な平面(黄色)
strokeWeight(1);
stroke(255,255,0);
for(int i=0; i<plot_num; i++){
for(int j=0; j<plot_num; j++){
plane_point.x = a.x;
plane_point.y = m_range + i*(p_range-m_range)/plot_num;
plane_point.z = m_range + j*(p_range-m_range)/plot_num;
point_rhs(plane_point.copy().mult(res));
}
}
// 点Aを通り、z軸に垂直な平面(水色)
stroke(0,255,255);
for(int i=0; i<plot_num; i++){
for(int j=0; j<plot_num; j++){
plane_point.x = m_range + i*(p_range-m_range)/plot_num;
plane_point.y = m_range + j*(p_range-m_range)/plot_num;
plane_point.z = a.z;
point_rhs(plane_point.copy().mult(res));
}
}
// 点Aを通り、zx平面に平行な平面(桃色)
stroke(255,0,255);
for(int i=0; i<plot_num; i++){
for(int j=0; j<plot_num; j++){
plane_point.x = m_range + i*(p_range-m_range)/plot_num;
plane_point.y = a.y;
plane_point.z = m_range + j*(p_range-m_range)/plot_num;
point_rhs(plane_point.copy().mult(res));
}
}
}ソースコード2 座標軸に垂直な平面を描くプログラム
このスケッチ「drawPlanes」を実行すると、図3のように、実行ウィンドウのキャンバスに空間の座標系を表す3つの空間ベクトル(赤色:$${x}$$軸、緑色:$${y}$$軸、青色:$${z}$$軸)を基準にして、$${x}$$軸に垂直な平面を黄色、$${z}$$軸に垂直な平面を水色、$${zx}$$平面に平行な平面を桃色で表示しています。
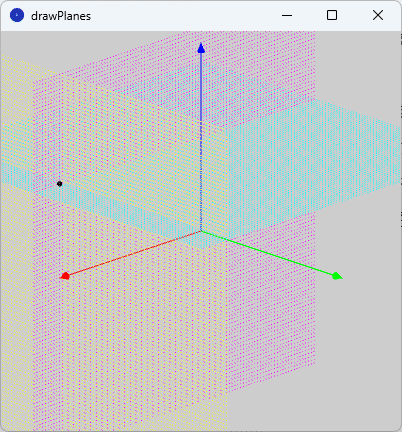
球面の方程式に関する問題
最後に、球面の方程式に関する問題を解くプログラムを作成していきます。
球面の方程式に関する問題
次のような球面の方程式を求めて、空間上に描け。
(1) 中心が原点、半径が$${2}$$の球面
(2) 中心が$${\mathrm{C}(1,2,3)}$$、半径が$${3}$$の球面
(3) 中心が$${\mathrm{C}(1,3,-1)}$$で、点$${\mathrm{A}(5,-1,1)}$$を通る球面
(4) 2点$${\mathrm{A}(-1,2,3),\mathrm{B}(3,6,-1)}$$を直径の両端とする球面
球面の方程式の導出
各問題の球面の方程式を求めていきます。
(1)の球面の方程式は、
$$
x^2+y^2+z^2=2^2
$$
です。(2)の球面の方程式は、
$$
(x-1)^2+(y-2)^2+(z-3)^2=3^2
$$
となります。(3)の球面の方程式は点Aを通るので、球面の半径$${r_3}$$は
$$
r_3 = \mathrm{ACの長さ} = 6
$$
となり、
$$
(x-1)^2+(y-3)^2+(z+1)^2=6^2
$$
となります。最後に、(4)の球面の方程式は、点$${\mathrm{A,B}}$$を直径の両端とするので、中心は線分$${\mathrm{AB}}$$の中点$${(1,4,1)}$$となり、半径は線分$${\mathrm{AB}}$$の長さの半分の$${2\sqrt{3}}$$となり、方程式は、
$$
(x-1)^2+(y-4)^2+(z-1)^2=12
$$
となります。
球面を描くプログラム
上記で各問題の球面の方程式は導出したので、あとはその球面を描くプログラムを作成していきます。なお、問題(3)と(4)について、半径や中心座標を求めていますが、プログラムで改めて計算するようにしています。
先程作成したスケッチ「plot3Dpoints」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「drawSpheres」と変更し、またスケッチ「drawSpheres」内の「plot3Dpoints.pde」ファイルの名前を「drawSpheres.pde」に変更します。そして、pdeファイル「drawSpheres.pde」をダブルクリックしてスケッチ「drawSpheres」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「drawSpheres」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
// 球面を描く
float range; // 座標系での表示範囲-range≦x,y.z≦range
float res; // 座標系のサイズをキャンバスのサイズに変換するパラメータ
float angle = 0.0;
PVector c1,c2,c3,c4; // 問題の球面の中心位置を表わすベクトル
float r1,r2,r3,r4;// 問題の球面の半径
PVector a3; // 問題(3)の点Aを表わすベクトル
PVector a4, b4; // 問題(4)の点A,Bを表わすベクトル
void setup(){
size(400, 400, P3D);
noFill();
ortho();
range = 10.0;
res = width / 2.0 / range;
// (1)中心が原点、半径が2の球面
c1 = new PVector(0.0,0.0,0.0);
r1 = 2.0;
// (2)中心がC(1,2,3)、半径が3の球面
c2 = new PVector(1.0,2.0,3.0);
r2 = 3.0;
// (3)中心がC(1,3,-1)で、点A(5,-1,1)を通る球面
a3 = new PVector(5.0,-1.0,1.0);
c3 = new PVector(1.0,3.0,-1.0);
r3 = a3.copy().sub( c3.copy() ).mag();
// (4)2点A(-1,2,3)、B(3,6,-1)を直径の両端とする球面
a4 = new PVector(-1.0,2.0,3.0);
b4 = new PVector(3.0,6.0,-1.0);
c4 = a4.copy().add( b4.copy() ).mult(0.5);
r4 = a4.copy().sub( b4.copy() ).mag()/2.0;
println("r3=", r3);
println("c4=", c4);
println("r4=", r4);
}
void draw(){
background(204); // 背景をグレーにする
// 視点を設定する
camera(200.0, -200.0, 100.0, 0.0, 0.0, 0.0, 0.0, 0.0, -1.0);
// マウスボタンが押されたときの処理
if(mousePressed){
if( mouseButton == LEFT ){ // 左ボタンがおされたときはz軸時計周りに回転
angle = angle + 1.0;
} else if( mouseButton == RIGHT ){ // 右ボタンがおされたときはz軸反時計周りに回転
angle = angle -1.0;
} else {
}
}
// z軸周りに回転
rotateZ(radians(angle));
// 座標軸の設定
fill(255,0,0);
stroke(255,0,0);
arrow3D(0.0,0.0,0.0,range * res,0.0,0.0); // x軸(赤色)
fill(0,255,0);
stroke(0,255,0);
arrow3D(0.0,0.0,0.0,0.0,range * res,0.0); // y軸(緑色)
fill(0,0,255);
stroke(0,0,255);
arrow3D(0.0,0.0,0.0,0.0,0.0,range * res); // z軸(青色)
noFill();
stroke(0,0,0);
// 以下に、図形を描いていく
// (1)中心が原点、半径が2の球面 (黄色)
strokeWeight(5);
stroke(255,255,0);
point_rhs(c1.copy().mult(res));
strokeWeight(1);
stroke(255,255,0,20);
noFill();
sphere_rhs(c1.copy().mult(res), r1*res);
// (2)中心がC(1,2,3)、半径が3の球面(水色)
strokeWeight(5);
stroke(0,255,255);
point_rhs(c2.copy().mult(res));
strokeWeight(1);
stroke(0,255,255,20);
noFill();
sphere_rhs(c2.copy().mult(res), r2*res);
// (3)中心がC(1,3,-1)で、点A(5,-1,1)を通る球面(桃色)
strokeWeight(5);
stroke(255,0,255);
point_rhs(c3.copy().mult(res));
point_rhs(a3.copy().mult(res));
strokeWeight(1);
stroke(255,0,255,20);
noFill();
sphere_rhs(c3.copy().mult(res), r3*res);
// (4)2点A(-1,2,3)、B(3,6,-1)を直径の両端とする球面(白色)
strokeWeight(5);
stroke(255,255,255);
point_rhs(a4.copy().mult(res));
point_rhs(b4.copy().mult(res));
strokeWeight(1);
stroke(255,255,255,50);
noFill();
sphere_rhs(c4.copy().mult(res), r4*res);
}ソースコード3 球面を描くプログラム
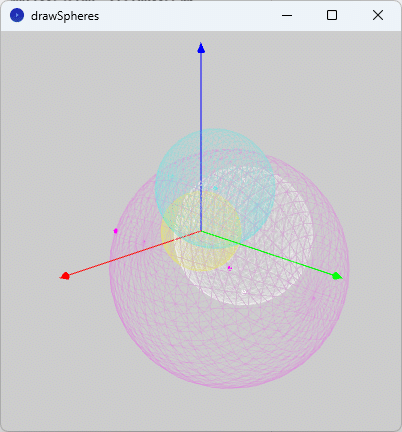
このスケッチ「drawSpheres」を実行すると、図4のように、実行ウィンドウのキャンバスに空間の座標系を表す3つの空間ベクトル(赤色:$${x}$$軸、緑色:$${y}$$軸、青色:$${z}$$軸)を基準にして、
(1) 中心が原点、半径が$${2}$$の球面を黄色、
(2) 中心が$${\mathrm{C}(1,2,3)}$$、半径が$${3}$$の球面を水色、
(3) 中心が$${\mathrm{C}(1,3,-1)}$$で、点$${\mathrm{A}(5,-1,1)}$$を通る球面を桃色、
(4) 2点$${\mathrm{A}(-1,2,3),\mathrm{B}(3,6,-1)}$$を直径の両端とする球面を白色
で表示しています。
まとめ
今回は、数学Bで学ぶ「座標空間における図形」について、線分の内分点や外分点の座標を計算して空間にプロットするプログラムや座標軸に垂直な平面を描くプログラム、そして球面を描くプログラムを作成しました。
いずれも描くこと自体は難しくはない方だと思いますが、点をプロットするときと平面や球面を描くときの線の太さを細かく調整しているので、そのあたりに注意して描く必要があるでしょう。
あと、実際に平面や球面を描いた図を見てみていかがでしょうか。味気ない方程式ですが図示してみると、意外にきれいで驚かないでしょうか。こういうことを感じることも、高校数学をプログラミングすることの醍醐味だと思っています。
参考文献
改訂版 教科書傍用 スタンダード 数学B(数研出版、ISBN9784410209468)
この記事が気に入ったらサポートをしてみませんか?
