
高校数学をプログラミングで解く(数学B編)「2-0-3 右手系で図形を描く」
マガジンリスト > 数学B編 2.空間のベクトル > 2-0-3 右手系で図形を描く
はじめに
今回は3次元空間に右手座標系で図形を描くために便利な関数を作成した上で、今後3次元空間に3次元の座標軸を用意して図形を描くためのテンプレートとなるスケッチを作成していきます。
3次元空間上に正三角形を描く
まず、3次元空間上に正三角形を描くプログラムを作成してみます。なお、正三角形は3つの頂点$${\mathrm{A}(5,0,0)}$$、$${\mathrm{B}(0,5,0)}$$、$${\mathrm{C}(0,0,5)}$$を線分で結んだものとします。
3次元空間上に正三角形を描くプログラム
記事『高校数学をプログラミングで解く(数学B編)「2-0-2 3次元空間での座標軸を準備する」』で利用したスケッチ「draw3DCoordinates」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「draw3DTriangle」と変更し、またスケッチ「draw3DTriangle」内の「draw3DCoordinates.pde」ファイルの名前を「draw3DTriangle.pde」に変更します。そして、pdeファイル「draw3DTriangle.pde」をダブルクリックしてスケッチ「draw3DTriangle」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「draw3DTriangle」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
float range; // 座標系での表示範囲-range≦x,y.z≦range
float res; // 座標系のサイズをキャンバスのサイズに変換するパラメータ
float angle = 0.0;
void setup(){
size(400, 400, P3D);
// noFill();
ortho();
range = 10.0;
res = width / 2.0 / range;
}
void draw(){
background(204); // 背景をグレーにする
// 視点を設定する
camera(width/2.0, -height/2.0, height/4.0, 0.0, 0.0, 0.0, 0.0, 0.0, -1.0);
// マウスボタンが押されたときの処理
if(mousePressed){
if( mouseButton == LEFT ){ // 左ボタンがおされたときはz軸時計周りに回転
angle = angle + 1.0;
} else if( mouseButton == RIGHT ){ // 右ボタンがおされたときはz軸反時計周りに回転
angle = angle -1.0;
} else {
}
}
// z軸周りに回転
rotateZ(radians(angle));
// 座標軸の設定
strokeWeight(1);
fill(255,0,0);
stroke(255,0,0);
arrow3D(0.0,0.0,0.0,range * res,0.0,0.0); // x軸(赤色)
fill(0,255,0);
stroke(0,255,0);
arrow3D(0.0,0.0,0.0,0.0,range * res,0.0); // y軸(緑色)
fill(0,0,255);
stroke(0,0,255);
arrow3D(0.0,0.0,0.0,0.0,0.0,range * res); // z軸(青色)
noFill();
stroke(0,0,0);
// 以下に図形を描いていく
// 三角形を描く
PVector a = new PVector(5.0, 0.0, 0.0);
PVector b = new PVector(0.0, 5.0, 0.0);
PVector c = new PVector(0.0, 0.0, 5.0);
beginShape();
vertex(a.x*res, a.y*res, a.z*res);
vertex(b.x*res, b.y*res, b.z*res);
vertex(c.x*res, c.y*res, c.z*res);
endShape(CLOSE);
}ソースコード1 3次元空間に正三角形を描くプログラム
このスケッチ「draw3DTriangle」を実行すると、図1のように実行ウィンドウのキャンバス上に$${x}$$軸を赤色の空間ベクトル、 $${y}$$軸を緑色の空間ベクトル、 $${z}$$軸を青色の空間ベクトルとして描かれた3次元空間での正三角形が描かれます。
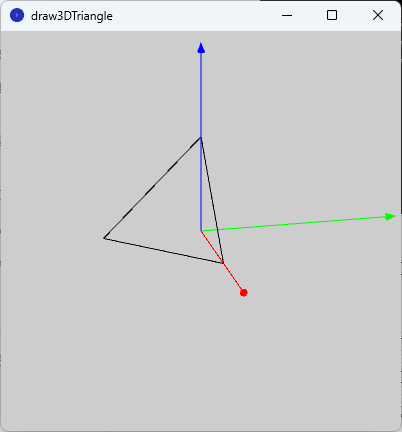
左手系で定義されている関数への対策
図1を見ると、正三角形の位置が想像していたものと異なっています。具体的には頂点$${\mathrm{B}}$$の位置が$${(0,5,0)}$$ではなく、$${(0,-5,0)}$$になっています。これは、vertex 関数がその引数として与えられる座標位置を”左手系"の座標として解釈することに起因します。つまり、頂点$${\mathrm{B}}$$の座標位置$${(0,5,0)}$$を”右手系”と解釈して入力したにもかかわらず、vertex 関数が"左手系"の座標位置として解釈したために起こりました。
これは、記事『高校数学をプログラミングで解く(準備編)「4-3 Processingでの3次元座標」』でも説明したように、入力された座標の$${y}$$成分の値を$${-y}$$と変換することで回避できます。実際に、ソースコード1の三角形を描く部分のコードを以下のように書き換えます。
// 三角形を描く
PVector a = new PVector(5.0, 0.0, 0.0);
PVector b = new PVector(0.0, 5.0, 0.0);
PVector c = new PVector(0.0, 0.0, 5.0);
beginShape();
vertex(a.x*res, -a.y*res, a.z*res);
vertex(b.x*res, -b.y*res, b.z*res);
vertex(c.x*res, -c.y*res, c.z*res);
endShape(CLOSE);ソースコード2 左手系で定義された関数への対策
この修正を行った上でスケッチ「draw3DTriangle」を実行すると、図2のように今度は実行ウィンドウのキャンバス上に想定の位置に正三角形が描かれます。
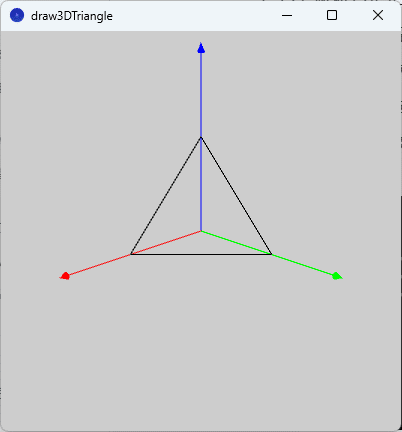
右手系の座標系で定義される関数の準備
上記で、右手系の座標で与えた正三角形の頂点の情報から Processing で準備された描画用関数(上記では vertex 関数)を利用して図形を描画する場合、入力された座標の$${y}$$成分の値を$${-y}$$と変換して描画用関数に入力することで右手系の座標系上で正しく描画することができることを見ました。ただ、今後も右手系で三角形を描く際に、常に座標の$${y}$$成分の値を$${-y}$$に変換することを意識しなければならないのは多少面倒です。
そこで、この座標変換を行った上で左手系での描画用関数を呼び出すことで右手系での図形を描く、この一連の処理を1つの関数としてまとめておくことにします。以下のソースコード3は右手座標系上に三角形を描くための一連の処理を1つの関数(関数名を triangle_rhs としています)にまとめたものになります。
// 右手座標系上に三角形を描く関数
void triangle_rhs(
PVector a,
PVector b,
PVector c
){
beginShape();
vertex(a.x, -a.y, a.z);
vertex(b.x, -b.y, b.z);
vertex(c.x, -c.y, c.z);
endShape(CLOSE);
}ソースコード3 右手座標系上に三角形を描く関数
なお、引数は三角形の3つの頂点の座標を表す PVector クラスの変数としています。
この triangle_rhs 関数をスケッチ「draw3DTriangle」に追加して右手座標系での正三角形を描いてみます。
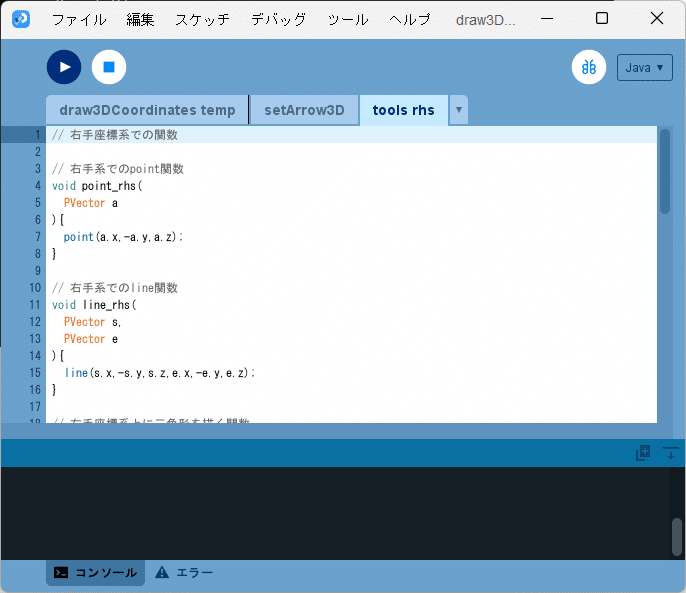
① スケッチ「draw3DTriangle」の開発環境ウィンドウのタブ欄にある▼のボタンを押して「新規タブ」を選択し、新たに「tools_rhs」タブを追加します(図3)。
② 「tools_rhs」タブを選択した状態で、そのテキストエディタ部分にtriangle_rhs 関数(ソースコード3)を記述します(図4)。
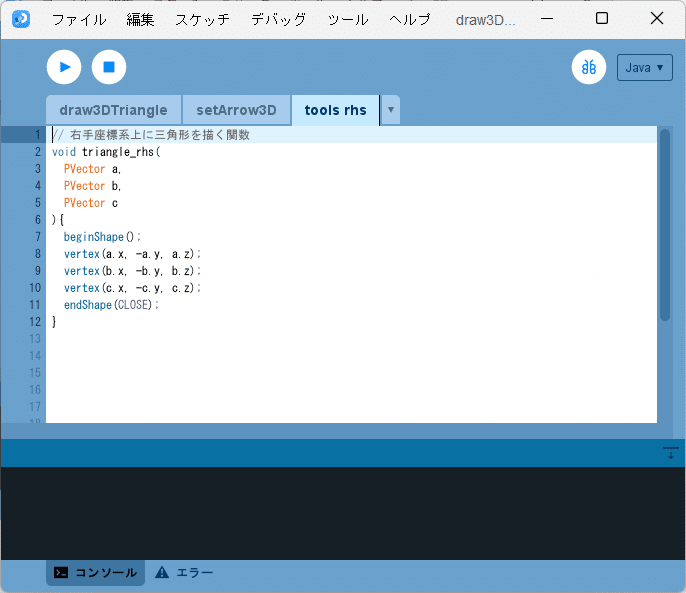
③ 「draw3DTriangle」タブを選択し、そのテキストエディタに記述されているコード(ソースコード1)の三角形を描く部分を以下のように書き換えます。
// 三角形を描く
PVector a = new PVector(5.0, 0.0, 0.0);
PVector b = new PVector(0.0, 5.0, 0.0);
PVector c = new PVector(0.0, 0.0, 5.0);
triangle_rhs(a.copy().mult(res),b.copy().mult(res),c.copy().mult(res));ソースコード4 triangle_rhs 関数を用いて三角形を描く
④ この状態でスケッチ「draw3DTriangle」を実行すると、実行ウィンドウのキャンバス上に図2と同じ正三角形が描かれます(図5)。
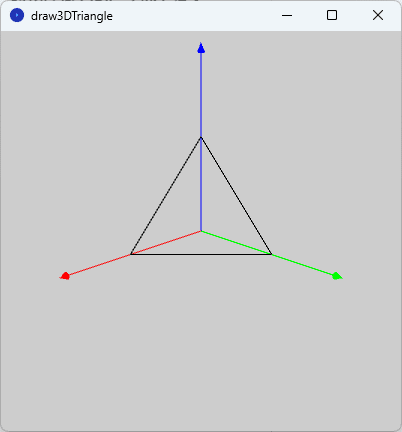
ソースコード4を見ると、draw 関数内では変数変換の処理を行っていないことがわかります。つまり、定義した右手座標系での描画用関数を用いることで、右手系と左手系との変換を意識することなく、右手座標系で図形を描くことができます。
右手座標系で図形を描くためのテンプレートの準備
最後に、三角形だけでなく、点、直線、四角形、球面についても変数変換を意識することなく右手座標系上に図形を描けるように関数化して準備しておきます。その上で、今後、右手座標系で図形を描いていくためのテンプレートとなるスケッチ「draw3DCoordinates_temp」を準備します。
右手座標系で各種図形を描くための関数と利用例
先ほど作成したスケッチ「draw3DTriangle」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「draw3DCoordinates_temp」と変更し、またスケッチ「draw3DCoordinates_temp」内の「draw3DTriangle.pde」ファイルの名前を「draw3DCoordinates_temp.pde」に変更します。そして、pdeファイル「draw3DTriangle.pde」をダブルクリックしてスケッチ「draw3DCoordinates_temp」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「tools_rhs」タブを選択し、そのテキストエリアのソースコードを以下のソースコード5で書き換えます。
// 右手座標系での関数
// 右手系でのpoint関数
void point_rhs(
PVector a
){
point(a.x,-a.y,a.z);
}
// 右手系でのline関数
void line_rhs(
PVector s,
PVector e
){
line(s.x,-s.y,s.z,e.x,-e.y,e.z);
}
// 右手座標系上に三角形を描く関数
void triangle_rhs(
PVector a,
PVector b,
PVector c
){
beginShape();
vertex(a.x, -a.y, a.z);
vertex(b.x, -b.y, b.z);
vertex(c.x, -c.y, c.z);
endShape(CLOSE);
}
// 右手座標系上に四角形を描く関数
void rect_rhs(
PVector a,
PVector b,
PVector c,
PVector d
){
beginShape();
vertex(a.x, -a.y, a.z);
vertex(b.x, -b.y, b.z);
vertex(c.x, -c.y, c.z);
vertex(d.x, -d.y, d.z);
endShape(CLOSE);
}
// 右手座標系上に球面を描く関数
void sphere_rhs(
PVector c, // 球面の中心座標
float r // 球面の半径
){
pushMatrix();
translate(c.x,-c.y,c.z);
sphere(r);
popMatrix();
}ソースコード5 右手系で点、直線、三角形、四角形、球面を描く関数
次に、開発環境ウィンドウのタブ欄で「draw3DCoordinates_temp」タブを選択し、そのテキストエリアのソースコードを以下のソースコード6で書き換えます。
float range; // 座標系での表示範囲-range≦x,y.z≦range
float res; // 座標系のサイズをキャンバスのサイズに変換するパラメータ
float angle = 0.0;
void setup(){
size(400, 400, P3D);
// noFill();
ortho();
range = 10.0;
res = width / 2.0 / range;
}
void draw(){
background(204); // 背景をグレーにする
// 視点を設定する
camera(width/2.0, -height/2.0, height/4.0, 0.0, 0.0, 0.0, 0.0, 0.0, -1.0);
// マウスボタンが押されたときの処理
if(mousePressed){
if( mouseButton == LEFT ){ // 左ボタンがおされたときはz軸時計周りに回転
angle = angle + 1.0;
} else if( mouseButton == RIGHT ){ // 右ボタンがおされたときはz軸反時計周りに回転
angle = angle -1.0;
} else {
}
}
// z軸周りに回転
rotateZ(radians(angle));
// 座標軸の設定
strokeWeight(1);
fill(255,0,0);
stroke(255,0,0);
arrow3D(0.0,0.0,0.0,range * res,0.0,0.0); // x軸(赤色)
fill(0,255,0);
stroke(0,255,0);
arrow3D(0.0,0.0,0.0,0.0,range * res,0.0); // y軸(緑色)
fill(0,0,255);
stroke(0,0,255);
arrow3D(0.0,0.0,0.0,0.0,0.0,range * res); // z軸(青色)
noFill();
stroke(0,0,0);
// 以下に図形を描いていく
// 点を描く
strokeWeight(5);
PVector p = new PVector(3.0,3.0,3.0);
point_rhs(p.copy().mult(res));
// 直線を描く
strokeWeight(1);
PVector s = new PVector(-5.0,-5.0,-3.0);
PVector e = new PVector(5.0,5.0,3.0);
line_rhs(s.copy().mult(res), e.copy().mult(res));
// 三角形を描く
strokeWeight(1);
PVector a = new PVector(5.0, 0.0, 0.0);
PVector b = new PVector(0.0, 5.0, 0.0);
PVector c = new PVector(0.0, 0.0, 5.0);
triangle_rhs(a.copy().mult(res),b.copy().mult(res),c.copy().mult(res));
// 四角形を描く
strokeWeight(1);
a = new PVector(4.0, 0.0, 0.0);
b = new PVector(0.0, 4.0, 0.0);
c = new PVector(0.0, 0.0, 4.0);
PVector d = new PVector(4.0, 4.0, -4.0);
rect_rhs(a.copy().mult(res),c.copy().mult(res),b.copy().mult(res),d.copy().mult(res));
// 球面を描く
strokeWeight(1);
stroke(128,128,128);
c = new PVector(0.0, 0.0, 7.5);
float r = 2.0;
sphere_rhs(c.copy().mult(res),r*res);
}ソースコード6 右手系で図形を描く関数の利用例
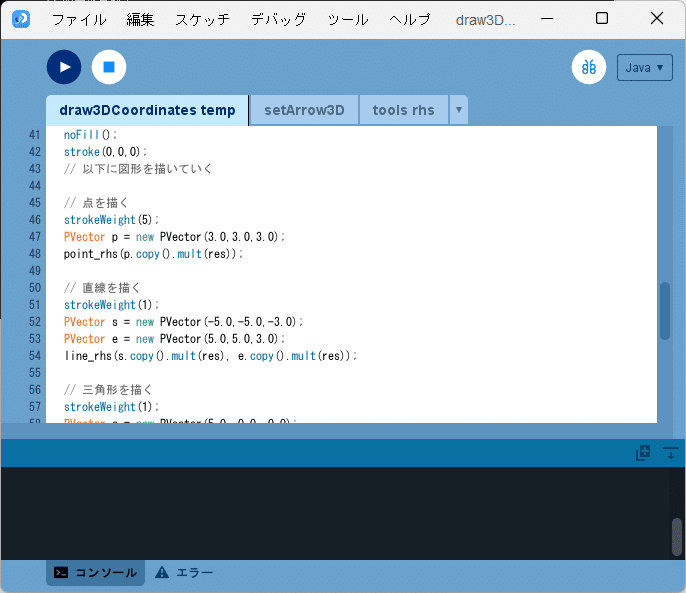
ソースコード5とソースコード6とを反映した上でスケッチ「draw3DCoordinates_temp」を実行すると、図8のように実行ウィンドウのキャンバス上に点、直線、三角形、四角形、球面が描かれます。
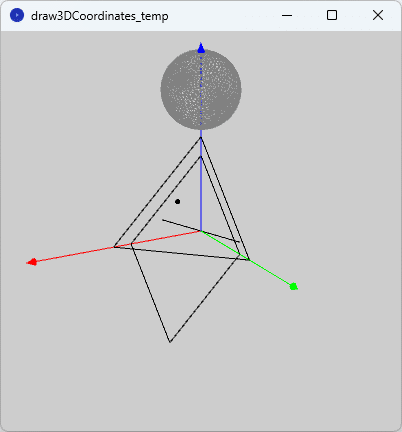
テンプレートとして利用する
今回作成したスケッチ「draw3DCoordinates_temp」は、そのフォルダごとコピーして、右手座標系で空間図形や空間ベクトルを描くためのテンプレートとして再利用することができます。その場合は、ソースコード6の
// 以下に図形を描いていく以下の部分を書き換えて利用します。
まとめ
今回は3次元空間に右手座標系で図形を描くために便利な関数を作成した上で、今後3次元空間に3次元の座標軸を用意して図形を描くためのテンプレートとなるスケッチ「draw3DCoordinates_temp」を作成しました。
今回作成したスケッチ「draw3DCoordinates_temp」の利用方法は今後、空間ベクトルや空間図形に関する記事で実際に利用していくので、そちらの記事も見てください。
参考文献
改訂版 教科書傍用 スタンダード 数学B(数研出版、ISBN9784410209468)
Processingをはじめよう 第2版(オライリー・ジャパン、オーム社、ISBN9784873117737)
