
高校数学をプログラミングで解く(準備編)「4-3 Processingでの3次元座標」
マガジンリスト > 準備編 4.動画、3次元表示 > 4-3 Processingでの3次元座標
はじめに
今回はProcessingで3次元座標を扱う方法について説明していきます。
3次元空間の座標系
これまでは2次元平面上の図形やベクトルを扱ってきました。ここでは3次元空間上の図形やベクトルを扱っていきます。今回はその準備として3次元空間の座標系について解説していきます。
Processingで3次元空間を扱うための設定
まず、Processingで3次元空間を扱うための設定について解説します。と言っても設定は簡単です。size関数の3つ目の引数に"P3D"を記述するだけです。
size(400,400,P3D);空間座標の特徴を見てみる
size関数の3つ目の引数に"P3D"を設定することで、空間上の図形などを扱えるようになりました。つまり、座標位置として$${x,y}$$に加えて$${z}$$軸方向の成分を持つことができます。
では、3次元空間上の座標がProcessingでどのように設定されているかを見ていきます。そのために、空間上に3次元座標の軸が設定されていると仮定してそれぞれの座標軸上に点列を描いてみます。
なお、点は記事『高校数学をプログラミングで解く(準備編)「2-1 Processingで図形を描く」』で紹介した point 関数を、3つ目の引数として$${z}$$軸方向の値を指定することで利用することができます。
point(x, y, z);x:点の位置の$${x}$$座標 float型
y:点の位置の$${y}$$座標 float型
z:点の位置の$${z}$$座標 float型
点列を描くプログラム
では、点列を描くプログラムを作成します。
void setup(){
size(400, 400, P3D); // 3次元空間を利用するためにP3Dを設定
noLoop();
// 点のサイズを設定
strokeWeight(10);
// 座標系の原点に点を打つ(黒色)
point(0.0,0.0,0.0);
// x軸上に点列を並べる(赤色)
stroke(255,0,0);
for(int i=1; i<=4; i++){
point(50.0*i,0.0,0.0);
}
// y軸上に点列を並べる(緑色)
stroke(0,255,0);
for(int i=1; i<=4; i++){
point(0.0,50.0*i,0.0);
}
// z軸上に点列を並べる(青色)
stroke(0,0,255);
for(int i=1; i<=4; i++){
point(0.0,0.0,50.0*i);
}
}ソースコード1 3次元空間上に点列を描くプログラム
プログラム(ソースコード1)では、座標軸の原点に黒色の点、$${x}$$軸上正の向きに座標軸の原点から50ピクセル間隔で4つの赤色の点、$${y}$$軸上正の向きに座標軸の原点から50ピクセル間隔で4つの緑色の点、$${z}$$軸上正の向きに座標軸の原点から50ピクセル間隔で4つの青色の点がそれぞれ並ぶようにキャンバス上に描いています。
このソースコード1を、Processingの開発環境ウィンドウを開いて(スケッチ名を「draw3DTest」としています)、テキストエディタ部分に書いて実行すると、図1のように実行ウィンドウのキャンバス上に点列が描かれます。

図1の結果を見ると、黒色の点がキャンバスの左上にあります。これは、座標系の原点がキャンバスの左上に位置していることを示しています。また、赤色の点列が左上の原点から右向きに打たれていることから、$${x}$$軸の正の向きが右向きになっていることがわかります。一方、緑色の点列が左上の原点から下向きに打たれていることから、$${y}$$軸の正の向きが下向きになっていることがわかります。青色の点列は描かれていないので、まだこの段階で$${z}$$軸の情報はわかりません。
点列を移動させてみる
ソースコード1では$${z}$$軸の情報がわかりませんでしたので、次に点列を移動させるとどうなるかを見てみます。具体的には、座標系の原点をキャンバスの中央に移動してみます。この原点の移動は、記事『高校数学をプログラミングで解く(数学A編)「2-0 高校数学に適した座標系の準備」』で紹介した translate 関数を利用できます。なお、3つ目の引数として$${z}$$軸方向の値を指定することで$${z}$$軸方向の移動も可能になります。
translate(x, y, z);各引数は次のようになっています。
x:$${x}$$方向の正の向きに移動させる幅 float型
y:$${y}$$方向の正の向きに移動させる幅 float型
z:$${z}$$方向の正の向きに移動させる幅 float型
では、ソースコード1の size 関数の下に、
translate(width/2.0, height/2.0, 0.0);を追加して、座標系の原点をキャンバスの中央に移動します。なお、今回は$${z}$$軸方向の移動はしていません。
translate 関数を追加後、スケッチ「draw3DTest」を実行すると、図2のように実行ウィンドウのキャンバスにキャンバスの中央と移動した点列が描かれます。
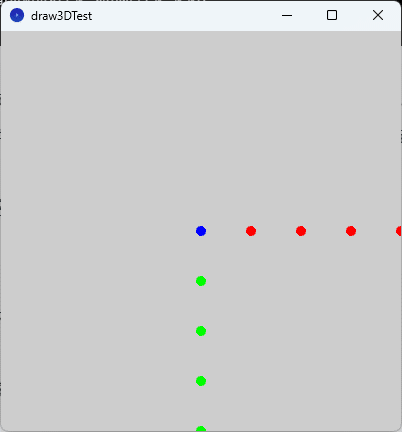
図2をよく見ると、キャンバスの中央の点が黒色ではなく、青色になっていることがわかります。これは、青色の点列が原点の位置でキャンバスから垂直手前方向に並ぶことによって起こっています。つまり、$${z}$$軸の正の向きがキャンバスから垂直手前方向に向いていることを示唆しています。また、このことからProcessingでの3次元座標系は左手系となっていることがわかります(左手系と右手系については後述)。
もう一つ、今度は座標系の原点をキャンバスの左上から$${x}$$軸正の向きに4分の1、$${y}$$軸正の向きに4分の1の位置に移動してみます。
ソースコード1の size 関数の下に入れた translate 関数を、
translate(width/4.0, height/4.0, 0.0);のように変更した後、スケッチ「draw3DTest」を実行すると、図3のように実行ウィンドウのキャンバスに移動した点列が描かれます。

図3では、$${z}$$軸方向の点列(青色)が見えました。ただ、座標系の原点(黒色)から左上の方向に点列が並んでいます。これは、空間座標がキャンバスの中央を消失点とする遠近法(透視投影法)を利用して描かれていることを示しています。
視点を考える
上記で、size 関数の3つ目の引数に”P3D"を設定すると、3次元座標系として原点がキャンバスの左上、$${x}$$軸の正の方向が右向き、$${y}$$軸の正の方向が下向き、そして$${z}$$軸の正の方向がキャンバスから垂直手前方向に向いていて、キャンバスの中央を消失点とする遠近法で描くように設定されていることがわかりました。
また、translate 関数を利用して3次元座標系を平行移動することができました。その他、(ここでは紹介しませんが、)3次元座標系の回転なども行うことができますので、3次元空間上の図形をいろいろな角度から見ることができます。
ただ、3次元の図形を様々な角度から見るために、3次元座標系を移動、回転させて調整することは結構大変な作業になります。そこで、次は、図形や3次元座標系を動かすのではなく、視点を変えることで3次元の図形をいろいろな角度からみることを考えます。
camera 関数
3次元空間で視点を設定するためには camera 関数を利用します。
camera(eyeX, eyeY, eyeZ, centerX, centerY, centerZ, upX, upY, upZ);各引数は次のようになっています。
eyeX:目(カメラ)の位置座標の$${x}$$成分 float型
eyeY:目(カメラ)の位置座標の$${y}$$成分 float型
eyeZ:目(カメラ)の位置座標の$${z}$$成分 float型
centerX:キャンバスの中心となる座標の$${x}$$成分 float型
centerY:キャンバスの中心となる座標の$${y}$$成分 float型
centerZ:キャンバスの中心となる座標の$${z}$$成分 float型
upX:座標軸の向きを決めるパラメータ 0.0 or 1.0 or -1.0 のいずれか float型
upY:座標軸の向きを決めるパラメータ 0.0 or 1.0 or -1.0 のいずれか float型
upZ:座標軸の向きを決めるパラメータ 0.0 or 1.0 or -1.0 のいずれか float型
図4に、この camera 関数を利用したときの概念図を示します。
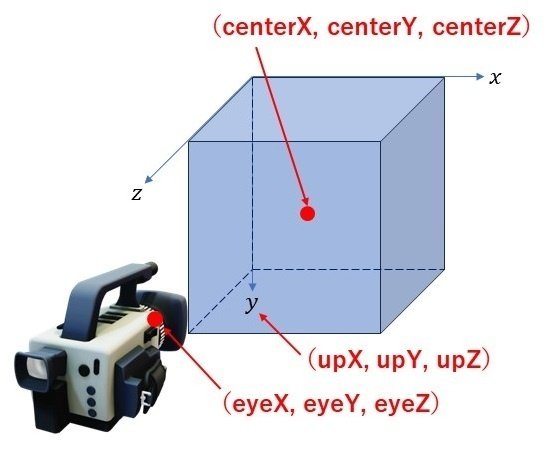
camera 関数を利用して3次元空間での視点を設定する方法を理解するために、以下の順で考えてみてください。
① まず、3次元座標系$${xyz}$$を設定します。このとき、例えば、(upX, upY, upZ)の値を(0.0,1.0,0.0)と設定すると、$${y}$$軸の正の向きが下向きになるように3次元座標系が設定されます。
② この3次元座標系を基準として、座標(eyeX, eyeY,eyeZ)の位置にカメラ(視点)を設定しています。
③ そして、座標(centerX, centerY, centerZ)の位置がキャンバスの中央にくるように、カメラの向き(視線)が設定されます。
camera 関数の初期設定
上記の3次元空間の座標系の節では、size 関数の3つ目の引数に"P3D"を設定するのみで、camera 関数を明示的に設定していませんでしたが、実は以下のような設定が暗黙的になされています。
camera(width/2, height/2, (height/2) / tan(PI/6), width/2, height/2, 0, 0, 1, 0);つまり、以下のように設定されています。
① 7つ目から9つ目の引数の値が(0,1,0)となっているので、$${y}$$軸の正の向きが下向きになるように3次元座標系が設定されます。
② 1つ目から3つ目の引数の値が(width/2, height/2, (height/2) / tan(PI/6))となっているので、①での3次元座標系を基準として、座標(width/2, height/2, (height/2) / tan(PI/6))の位置にカメラ(視点)が設定されます。
③ そして、4つ目から6つ目の引数の値が(width/2, height/2, 0)となっているので、座標(width/2, height/2, 0)の位置がキャンバスの中央にくるように、カメラの向き(視線)が設定されます。
この設定を3次元空間の座標系の節の内容と比較してみます。
①で$${y}$$軸の正の向きが下向きになるように3次元座標系が設定されます。また、②③で視点の座標が(width/2, height/2, (height/2) / tan(PI/6))、キャンバスの中央位置の座標が(width/2, height/2, 0)と設定されているので、視線は$${z}$$軸と並行になることがわかります。そして、Processingの3次元座標系が左手系であることを考慮すると、$${x}$$軸の正の向きが右向きになることがわかります。
以上のことから、3次元座標の原点(0,0,0)は左上にくることがわかり、これは図1と矛盾しないことがわかります。また、視線が$${z}$$軸と並行であることから、図2とも矛盾しないことがわかります。
左手系と右手系
3次元座標系の取り方として、大きく左手系と右手系の2つの方法があります。図5の左図が左手系の3次元座標系、右図が右手系の3次元座標系になります。

なぜ、これらの座標系が左手系や右手系と呼ばれるかということを説明します。
まず、手を握った状態から親指を立てます。次に、人差し指を立てます。このとき、親指と人差し指が互いに垂直になるようにします。最後に、中指を立てます。このとき、中指が親指と人差し指と垂直になるようにします(物理の「フレミングの左手の法則」を知っている方はその指の形と同じものです)。
この状態で、親指を$${x}$$軸の正の向き、人差し指を$${y}$$軸の正の向きと合わせてみてください。このとき、中指が$${z}$$軸の正の方向と一致するのが左手だった場合その座標系を左手系と呼び、右手だった場合その座標系を右手系と呼びます。
高校数学は右手系
一般に、高校数学では右手系を利用します。一方で、Processingでの3次元座標系は左手系になっています。
残念ながら、Processingでは左手系を右手系に反転させるような関数など準備されていないようです。ただ、左手系で描かれた図形をあたかも右手系で描かれた図形とみなすようにすることはできます。
例えば、右手系の3次元座標系上の点$${(a,b,c)}$$を考えます(図6右図)。この点は右手系の3次元座標系を$${y}$$軸のみ正負反転させた左手系の3次元座標系でみると、座標$${(a,-b,c)}$$の位置にあることになります(図6左図)。
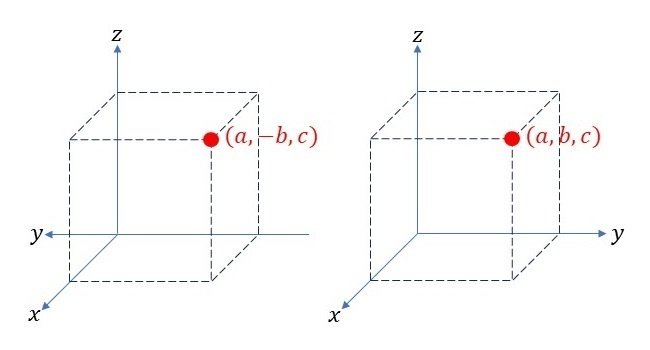
このことを利用すると、右手系の座標として入力したものをプログラムの中で$${y}$$座標成分のみ符号を反転させた上でキャンバスに表示すれば、あたかも右手系の3次元座標系上でプロットしたように考えることができます。今後、プログラムでは、入力された座標の$${y}$$成分の値を$${-y}$$と変換することで、右手系の3次元座標系を表現することにします。
透視投影と平行投影
図3で見たように、キャンバス上に描かれる図形は遠近法(透視投影法)で描かれます。ただ、高校数学で扱う3次元空間を表現するには、遠近法はあまり向いていません。そこで、遠近法(透視投影法)ではなく、平行投影法を利用してキャンバス上に図形を描くようにします。
平行投影法を利用するには、ortho 関数を利用します。
ortho();引数はありません。
では、図3を遠近法ではなく、平行投影法を用いて表示してみます。ソースコード1の size 関数の下に、
translate(width/4.0, height/4.0, 0.0);
ortho();を追加して、スケッチ「draw3DTest」を実行すると、図7のように実行ウィンドウのキャンバスに点列が描かれます。
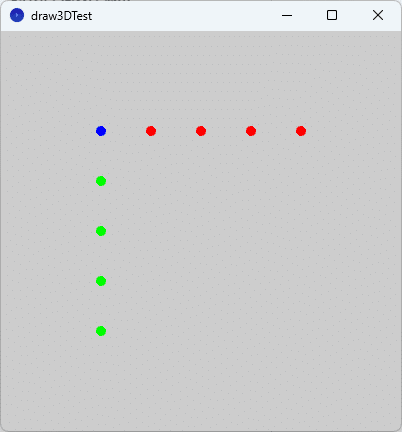
図3と図7と比較すると、$${z}$$軸方向の点列について座標系の原点(黒色)から左上の方向に並んでいた点列(図3)が、キャンバスから垂直手前方向に並ぶ(図7の青点)ように変わっていることがわかります。これは、図7が平行投影法で描かれていることを示しています。
高校数学に適した3次元座標系を考える
この記事の最後に、高校数学に適した3次元座標系を考えます。このような座標系の条件は以下の通りとします。
① $${z}$$軸の正の向きが上向き
② 視点は$${x>0, y>0, z>0}$$の領域
③ キャンバスの中心は座標軸の原点
④ 座標系は右手系
⑤ 平行投影法で描画
点列を描くプログラムの書き換え
これらの条件を満たす3次元座標系になるように、点列を描くプログラム(ソースコード1)を書き換えてみます。
void setup(){
size(400, 400, P3D); // 3次元空間を利用するためにP3Dを設定
noLoop();
// 視点を設定する
camera(width/2.0, -height/2.0, height/4.0, 0.0, 0.0, 0.0, 0.0, 0.0, -1.0);
// 平行投影法で描く
ortho();
// 点のサイズを設定
strokeWeight(10);
// 座標系の原点に点を打つ(黒色)
point(0.0,0.0,0.0);
// x軸上に点列を並べる(赤色)
stroke(255,0,0);
for(int i=1; i<=4; i++){
point(50.0*i,0.0,0.0);
}
// y軸上に点列を並べる(緑色)
stroke(0,255,0);
for(int i=1; i<=4; i++){
point(0.0,-50.0*i,0.0);
}
// z軸上に点列を並べる(青色)
stroke(0,0,255);
for(int i=1; i<=4; i++){
point(0.0,0.0,50.0*i);
}
}ソースコード2 点列を描くプログラム(書き換え)
このソースコード2に、スケッチ「draw3DTest」のテキストエディタ部分を書き換えて実行すると、図8のように実行ウィンドウのキャンバス上に点列が描かれます。

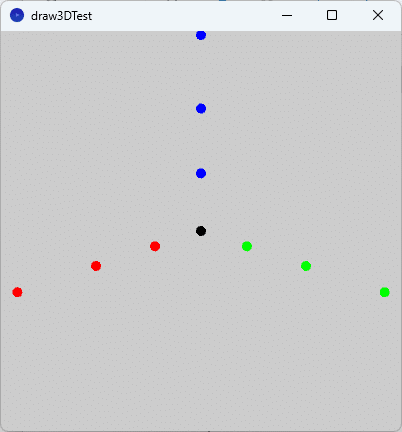
図8を見ると、高校数学に適した3次元座標系の条件①-⑤を満たすものとなっています。
プログラムの解説
ソースコード2について、解説しておきます。
まず、条件①-④は
camera(width/2.0, -height/2.0, height/4.0, 0.0, 0.0, 0.0, 0.0, 0.0, -1.0);の部分で実現されています。つまり、以下のように設定されています。
① 7つ目から9つ目の引数の値が(0,0,-1)となっているので、$${z}$$軸の正の向きが上向きになるように3次元座標系が設定されます。
② 1つ目から3つ目の引数の値が(width/2.0, -height/2.0, height/4.0)となっているので、①での3次元座標系を基準として、座標(width/2.0, -height/2.0, height/4.0)の位置にカメラ(視点)が設定されます。なお、条件④の右手系の座標系での扱いとするために、$${y}$$成分(2つ目の引数)の値の符号を反転していることに注意してください(詳細は、左手系と右手系の節をご覧ください)。これにより、視点は$${x>0, y>0, z>0}$$の領域となります。
③ そして、4つ目から6つ目の引数の値が(0, 0, 0)となっているので、原点の位置がキャンバスの中央にくるように、カメラの向き(視線)が設定されます。
次に、条件⑤については、
ortho();を記述することで実現されます。図8をみると、平行投影法での描画となっていることがわかります。ちなみに、ortho 関数を設定せず遠近法(透視投影法)を利用した場合の点列は図9のようになります。
最後に、条件④についてもう一つ説明しておきます。ソースコード2の
// y軸上に点列を並べる(緑色)
stroke(0,255,0);
for(int i=1; i<=4; i++){
point(0.0,-50.0*i,0.0);
} の部分を見てください。point 関数の2つ目の引数の符号をマイナスにしています。これは、右手系の座標系での扱いにするためにおこなっています(詳細は、左手系と右手系の節をご覧ください)。つまり、何らかの図形を描くときに座標の指定が必要な場合、$${y}$$成分の値の符号を反転させることに注意してください。
まとめ
今回はProcessingで3次元座標を扱う方法について説明しました。
Prcessingでの3次元座標は、size 関数に3つ目の引数として"P3D"を設定することで利用することができます。そして、camera 関数を用いると3次元座標系の視点を変えることができ、ortho 関数を用いると遠近法(透視投影法)から平行投影法に3次元空間の見方を変えることができました。
Processingでは左手系から右手系へ切り替えるような関数は用意されていないので、左手系で描いた図形をあたかも右手系で描いた図形であるように見なす方法についても説明しました。
これらの考察をもとにして、最後に、高校数学に適した3次元座標系について考えました。
高校数学に適した3次元座標系については数学B編でもう少し利用しやすいようにしていきます。ただ、3次元空間を扱うための基本的な情報としてはこの記事の内容を知っておけばよいでしょう。
参考文献
Processingの公式リファレンス「 Reference / Processing.org」
Processingをはじめよう 第2版(オライリー・ジャパン、オーム社、ISBN9784873117737)
この記事が気に入ったらサポートをしてみませんか?
