高校数学をプログラミングで解く(数学B編)「2-1 空間の座標」
マガジンリスト > 数学B編 2.空間のベクトル > 2-1 空間の座標
はじめに
今回は、数学Bで学ぶ「空間の座標」について、空間上に三角形を描いてその形状を調べる問題や空間上の点の座標を求める問題をプログラミングして考えてみます。
空間の座標
まず、空間の座標についてまとめておきます。
空間の点の座標
① 座標 3つの実数の組$${ (a,b,c) }$$で、空間の点の座標が定まる。
② $${x}$$軸上の点$${(a,0,0)}$$ $${y}$$軸上の点$${(0,b,0)}$$ $${z}$$軸上の点$${(0,0,c)}$$
③ $${xy}$$平面上の点$${(a,b,0)}$$ $${yz}$$平面上の点$${(0,b,c)}$$
$${zx}$$平面上の点$${(a,0,c)}$$
2点間の距離
$${\mathrm{A}(x_1, y_1, z_1)}$$、$${\mathrm{B}(x_2, y_2, z_2)}$$とする。
$$
\mathrm{AB} = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}, \mathrm{OA}=\sqrt{x_1^2+y_1^2+z_1^2}
$$
以下では、空間の座標を利用した問題をプログラムで解くことを考えてみます。
問題1 空間上の三角形の形状
次の3点を頂点とする$${\triangle \mathrm{ABC}}$$はどのような形の三角形か。
(1) $${\mathrm{A}(1,1,5)}$$、$${\mathrm{B}(4,3,-1)}$$、$${\mathrm{C}(-2,1,2)}$$
(2) $${\mathrm{A}(1,2,3)}$$、$${\mathrm{B}(3,1,5)}$$、$${\mathrm{C}(2,4,3)}$$
三角形を描くプログラム
問題1の三角形は空間上に浮かぶ三角形となります。この三角形がどのような三角形であるか、実際に描いて形状を見ることができるプログラムを作成します。まず、問題1(1)から作成してみます。
記事『高校数学をプログラミングで解く(数学B編)「2-0-3 右手系で図形を描く」』で作成したスケッチ「draw3DCoordinates_temp」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「drawTriangle3D」と変更し、またスケッチ「drawTriangle3D」内の「draw3DCoordinates_temp.pde」ファイルの名前を「drawTriangle3D.pde」に変更します。そして、pdeファイル「drawTriangle3D.pde」をダブルクリックしてスケッチ「drawTriangle3D」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「drawTriangle3D」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
float range; // 座標系での表示範囲-range≦x,y.z≦range
float res; // 座標系のサイズをキャンバスのサイズに変換するパラメータ
float angle = 0.0;
PVector a,b,c; // 空間の座標
void setup(){
size(400, 400, P3D);
noFill();
ortho();
range = 10.0;
res = width / 2.0 / range;
// △ABCの頂点の位置ベクトル
a = new PVector(1.0, 1.0, 5.0);
b = new PVector(4.0, 3.0, -1.0);
c = new PVector(-2.0, 1.0, 2.0);
// △ABCの各辺の長さ
float AB = sqrt((b.x-a.x)*(b.x-a.x) + (b.y-a.y)*(b.y-a.y) + (b.z-a.z)*(b.z-a.z));
float BC = sqrt((c.x-b.x)*(c.x-b.x) + (c.y-b.y)*(c.y-b.y) + (c.z-b.z)*(c.z-b.z));
float CA = sqrt((a.x-c.x)*(a.x-c.x) + (a.y-c.y)*(a.y-c.y) + (a.z-c.z)*(a.z-c.z));
println("AB:", AB);
println("BC:", BC);
println("CA:", CA);
}
void draw(){
background(204); // 背景をグレーにする
// 視点を設定する
camera(200.0, -200.0, 100.0, 0.0, 0.0, 0.0, 0.0, 0.0, -1.0);
// マウスボタンが押されたときの処理
if(mousePressed){
if( mouseButton == LEFT ){ // 左ボタンがおされたときはz軸時計周りに回転
angle = angle + 1.0;
} else if( mouseButton == RIGHT ){ // 右ボタンがおされたときはz軸反時計周りに回転
angle = angle -1.0;
} else {
}
}
// z軸周りに回転
rotateZ(radians(angle));
// 座標軸の設定
strokeWeight(1);
fill(255,0,0);
stroke(255,0,0);
arrow3D(0.0,0.0,0.0,range * res,0.0,0.0); // x軸(赤色)
fill(0,255,0);
stroke(0,255,0);
arrow3D(0.0,0.0,0.0,0.0,range * res,0.0); // y軸(緑色)
fill(0,0,255);
stroke(0,0,255);
arrow3D(0.0,0.0,0.0,0.0,0.0,range * res); // z軸(青色)
noFill();
stroke(0,0,0);
// 以下に、図形を描いていく
// △ABCの頂点をプロットする
strokeWeight(5);
stroke(0,0,0);
point_rhs(a.copy().mult(res));
point_rhs(b.copy().mult(res));
point_rhs(c.copy().mult(res));
// △ABCを描く
strokeWeight(1);
triangle_rhs(a.copy().mult(res),b.copy().mult(res),c.copy().mult(res));
}ソースコード1 空間上に三角形を描くプログラム
ソースコード1では、setup 関数と draw 関数の両方で利用する PVector クラスの変数の定義を関数外で行い、setup 関数内で各頂点ベクトルの設定や各辺の長さを計算してその結果をコンソールに出力し、繰り返し実行を行う draw 関数内で三角形を図示するようにしています。これにより、図示した三角形は角度を変えてみることができるようになります。
このスケッチ「drawTriangle3D」を実行すると、図1のように、実行ウィンドウのキャンバスに空間の座標系を表す3つの空間ベクトル(赤色:$${x}$$軸、緑色:$${y}$$軸、青色:$${z}$$軸)を基準にして、3つの点とそれらを頂点とする三角形が描かれます。
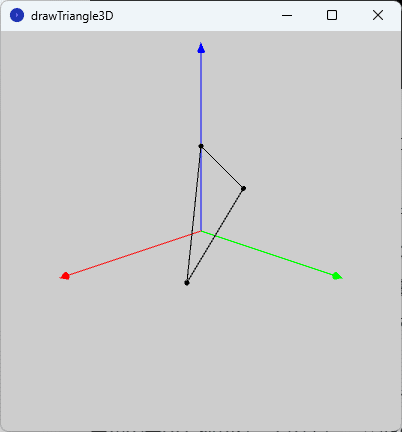
なお、キャンバス上を左クリックすると図形が$${z}$$軸を中心に時計回りに回転し、右クリックすると図形が$${z}$$軸を中心に反時計回りに回転します。回転させながらこの三角形を見てみると、この三角形が二等辺三角形であることがわかります。
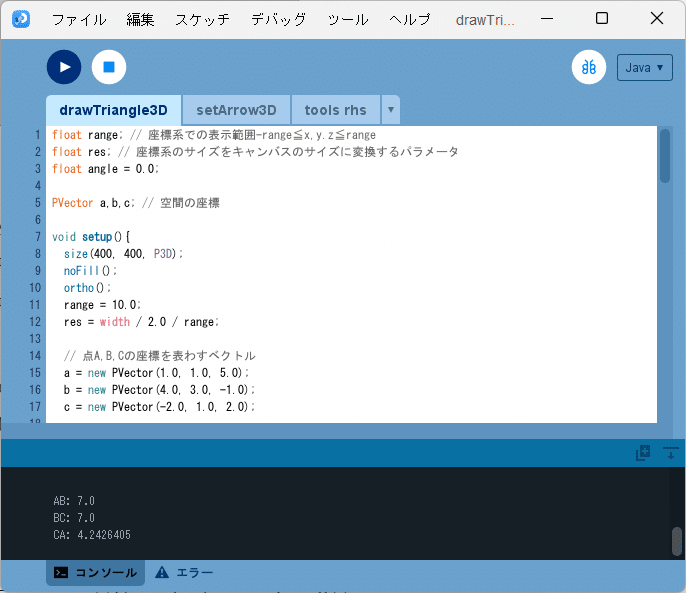
ソースコード1では$${\triangle \mathrm{ABC}}$$の各辺の長さを計算しており、それをコンソールに出力しています(図2)。その結果を見ると、
AB: 7.0
BC: 7.0
CA: 4.2426405
となって$${\mathrm{AB}=\mathrm{BC}}$$を満たしており、$${\triangle \mathrm{ABC}}$$が計算上も二等辺三角形になっていることがわかります。
同様にして、問題1(2)についても考えています。ソースコード1の
// △ABCの頂点の位置ベクトル
a = new PVector(1.0, 1.0, 5.0);
b = new PVector(4.0, 3.0, -1.0);
c = new PVector(-2.0, 1.0, 2.0);の部分を
// △ABCの頂点の位置ベクトル
a = new PVector(1.0, 2.0, 3.0);
b = new PVector(3.0, 1.0, 5.0);
c = new PVector(2.0, 4.0, 3.0);に書き換えて、このスケッチ「drawTriangle3D」を実行すると、図3のように、実行ウィンドウのキャンバスに三角形が描かれます。
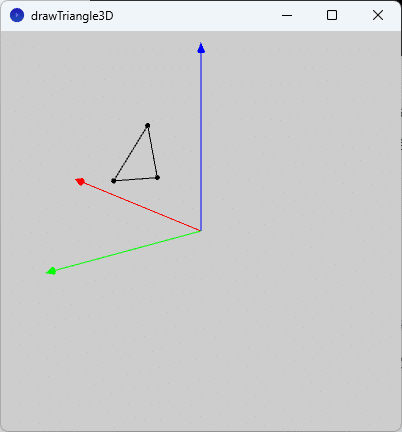
問題1(1)の時と同様に、回転させながらこの三角形を見てみると、この三角形が直角三角形であることがわかります。
ソースコード1のコンソール出力部分( println 関数を利用した部分)を少し書き換えて、$${\triangle \mathrm{ABC}}$$の各辺の長さの2乗も出力するようにすると、図4のように、コンソールに
AB: 3.0 ABの2乗: 9.0
BC: 3.7416575 BCの2乗: 14.000001
CA: 2.236068 CAの2乗: 5.0
と出力され、三平方の定理$${\mathrm{AB}^2+\mathrm{CA}^2=\mathrm{BC}^2}$$が成り立っていることがわかります。
問題2 空間上の点の座標を求める
3点$${\mathrm{A}(3,1,2)}$$、$${\mathrm{B}(-1,3,0)}$$、$${\mathrm{C}(2,-1,1)}$$から等距離にある$${yz}$$平面上の点の座標を求めよ。
今回は、この解となる点の座標を求める過程で出てくる平面や直線の式を図示しながら考えていきます。
問題2の解法
求める点の座標を$${\mathrm{P}(x,y,z)}$$とします。
① 点$${\mathrm{P}}$$と3点$${\mathrm{A,B,C}}$$それぞれの距離の2乗を計算します。
$$
\begin{array}{lll}
\mathrm{AP}^2 &=& (x-3)^2+(y-1)^2+(z-2)^2 \\
\mathrm{BP}^2 &=& (x+1)^2+(y-3)^2+z^2 \\
\mathrm{CP}^2 &=& (x-2)^2+(y+1)^2+(z-1)^2
\end{array}
$$
② 点$${\mathrm{P}}$$は3点から等距離にあるので、$${\mathrm{AP}=\mathrm{BP}}$$より$${\mathrm{AP}^2=\mathrm{BP}^2}$$となります。この式に①で求めた式を代入して整理すると、
$$
z = -2x+y+1
$$
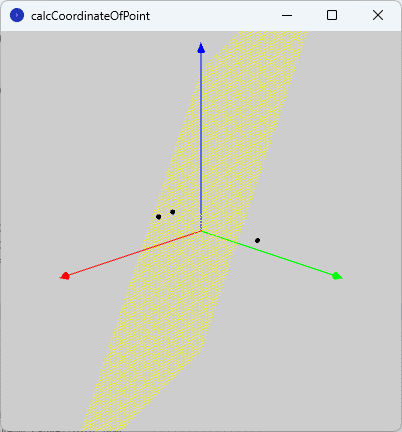
という式が得られます。この式は平面の式を表しており、実際に図示してみると、図5のような平面(黄色)になります。
③ ②と同様に、点$${\mathrm{P}}$$は3点から等距離にあるので、$${\mathrm{AP}=\mathrm{CP}}$$より$${\mathrm{AP}^2=\mathrm{CP}^2}$$となります。この式に①で求めた式を代入して整理すると、
$$
z = -x-2y+4
$$
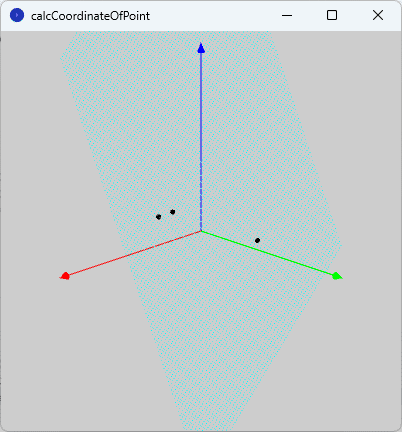
という式が得られます。この式も平面の式を表しており、実際に図示してみると、図6のような平面(水色)になります。
④ ②と③で求めた式を連立させると、
$$
y=\frac{1}{3} x + 1, \ z = -\frac{5}{3}x+2
$$
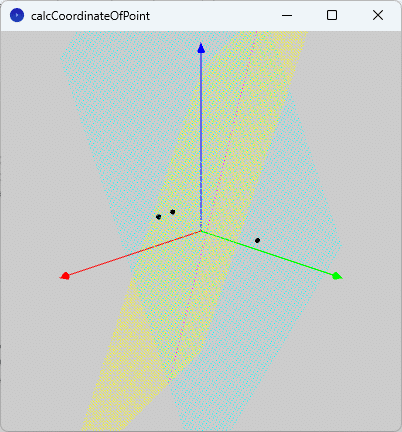
の2式が得られます。これらの式は②と③の平面が交わる直線を表します。実際に図示してみると、図7のような直線(桃色)になります。
⑤ 最後に、点$${\mathrm{P}}$$は$${yz}$$平面上の点であるので、$${x=0}$$とおくと、
$$
\mathrm{P}(0,1,2)
$$
が得られます。点$${\mathrm{P}}$$を図示すると、図8のような点(白色)になります。
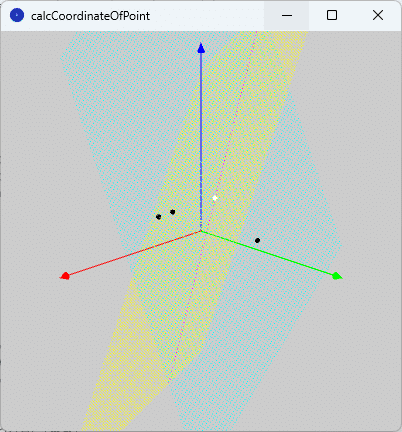
問題2のプログラム
図8を描くためのプログラムを示しておきます。
記事『高校数学をプログラミングで解く(数学B編)「2-0-3 右手系で図形を描く」』で作成したスケッチ「draw3DCoordinates_temp」をフォルダごとコピーして、スケッチの名前(フォルダ名)を「calcCoordinateOfPoint」と変更し、またスケッチ「calcCoordinateOfPoint」内の「draw3DCoordinates_temp.pde」ファイルの名前を「calcCoordinateOfPoint.pde」に変更します。そして、pdeファイル「calcCoordinateOfPoint.pde」をダブルクリックしてスケッチ「calcCoordinateOfPoint」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「calcCoordinateOfPoint」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。
float range; // 座標系での表示範囲-range≦x,y.z≦range
float res; // 座標系のサイズをキャンバスのサイズに変換するパラメータ
float angle = 0.0;
PVector a,b,c; // 空間の座標
void setup(){
size(400, 400, P3D);
noFill();
ortho();
range = 10.0;
res = width / 2.0 / range;
// 点A,B,Cの座標を表わすベクトル
a = new PVector(3.0, 1.0, 2.0);
b = new PVector(-1.0, 3.0, 0.0);
c = new PVector(2.0, -1.0, 1.0);
}
void draw(){
background(204); // 背景をグレーにする
// 視点を設定する
camera(200.0, -200.0, 100.0, 0.0, 0.0, 0.0, 0.0, 0.0, -1.0);
// マウスボタンが押されたときの処理
if(mousePressed){
if( mouseButton == LEFT ){ // 左ボタンがおされたときはz軸時計周りに回転
angle = angle + 1.0;
} else if( mouseButton == RIGHT ){ // 右ボタンがおされたときはz軸反時計周りに回転
angle = angle -1.0;
} else {
}
}
// z軸周りに回転
rotateZ(radians(angle));
// 座標軸の設定
strokeWeight(1);
fill(255,0,0);
stroke(255,0,0);
arrow3D(0.0,0.0,0.0,range * res,0.0,0.0); // x軸(赤色)
fill(0,255,0);
stroke(0,255,0);
arrow3D(0.0,0.0,0.0,0.0,range * res,0.0); // y軸(緑色)
fill(0,0,255);
stroke(0,0,255);
arrow3D(0.0,0.0,0.0,0.0,0.0,range * res); // z軸(青色)
noFill();
stroke(0,0,0);
// 以下に、図形を描いていく
// 3点A,B,Cを描く(黒色)
strokeWeight(5);
stroke(0,0,0);
point_rhs(a.copy().mult(res));
point_rhs(b.copy().mult(res));
point_rhs(c.copy().mult(res));
// 平面上の点を表す座標
PVector plane_point = new PVector(0.0,0.0,0.0);
// 平面を点群で表わすときの各軸方向に並べる点の数
int plot_num = 100;
// 図形を描く範囲
float m_range = -range/2.0;
float p_range = range/2.0;
// AP=BPを満たす平面(黄色)
strokeWeight(1);
stroke(255,255,0);
for(int i=0; i<plot_num; i++){
for(int j=0; j<plot_num; j++){
plane_point.x = m_range + i*(p_range-m_range)/plot_num;
plane_point.y = m_range + j*(p_range-m_range)/plot_num;
plane_point.z = -2.0 * plane_point.x + plane_point.y + 1.0;
point_rhs(plane_point.copy().mult(res));
}
}
// AP=CPを満たす平面(水色)
stroke(0,255,255);
for(int i=0; i<plot_num; i++){
for(int j=0; j<plot_num; j++){
plane_point.x = m_range + i*(p_range-m_range)/plot_num;
plane_point.y = m_range + j*(p_range-m_range)/plot_num;
plane_point.z = - plane_point.x -2.0 * plane_point.y + 4.0;
point_rhs(plane_point.copy().mult(res));
}
}
// 2つの平面が交わる線(桃色)
stroke(255,0,255);
for(int i=0; i<plot_num; i++){
plane_point.x = m_range + i*(p_range-m_range)/plot_num;
plane_point.y = plane_point.x / 3.0 + 1.0;
plane_point.z = -5.0/3.0 * plane_point.x + 2.0;
point_rhs(plane_point.copy().mult(res));
}
// 上記の直線とyz平面が交わる点P(白色)
stroke(255,255,255);
strokeWeight(5);
PVector p = new PVector(0.0,0.0,0.0);
p.x = 0.0;
p.y = p.x / 3.0 + 1.0;
p.z = -5.0/3.0 * p.x + 2.0;
point_rhs(p.copy().mult(res));
}ソースコード2 空間上に三角形を描くプログラム
このスケッチ「calcCoordinateOfPoint」を実行すると、図8のような図形がキャンバス上に描かれます。なお、「問題2の解法」の節で示した平面や直線は図形を回転させながら見た方が状況を把握しやすいので、実際にプログラムを実行させて、キャンバスをクリックしながら見てみてください。
プログラムの解説「平面の描画」
このプログラムでは、平面を小さな点を平面上に並べることで表現しています。こうした理由は、空間上に浮かんでいる平面を表すために、少し透過した形で表現したかったからです。
具体的には、$${xy}$$平面上の領域(今回は$${-\mathrm{range}/2 \leq x, y \leq \mathrm{range}/2}$$)に等間隔に碁盤目状に点を並べて(今回は$${100 \times 100}$$)、それぞれの点$${(x,y)}$$に対して平面の方程式から$${z}$$の値を求めて、その空間の座標$${(x,y,z)}$$をプロットしていくことで実現しています。
まとめ
今回は、数学Bで学ぶ「空間の座標」について、空間上に三角形を描いてその形状を調べる問題や空間上の点の座標を求める問題をプログラミングして考えてみました。
空間上の点や直線、平面を画面上に描くことはできますが、一面的にみると空間的な配置がよくわかりません。ただ、今回のように空間的に図形を回転することで図形の配置が少しはわかりやすくなったのではないでしょうか。図形の問題はプログラミングして実際に描いていくことで理解しやすくなりますので、ぜひそのスキルを高めていってください。
参考文献
改訂版 教科書傍用 スタンダード 数学B(数研出版、ISBN9784410209468)
