
大人の数学2 九九 から 十九十九 へ
はじめまして!
勉強、お仕事たいへんお疲れさまです。
このシリーズ記事は、数字の特徴に敏感になり、数値の扱いや計算を速くするための講座です。
新しい考え方を学び
『数字を上手に扱うための思考』をきたえます
公務員試験、就職試験、資格試験、あるいは中学受験など、スキルアップが必要なさまざまな場面にご活用ください。軽く読む内容ではなく、講座の形式を取っております。少しずつ新しい観点を学び、思考回路を変えていきましょう!
今回のテーマは、「九九 から 十九十九 へ」です。
もはやなんと読むかも分からない・・・
どこかの国では、九九を 2桁(10の位どうし)まで習うとか!?
でも、2桁×2桁をする機会、あると思います!
いろいろな問題を解いたりしますと、どうしても避けて通れないのが「2桁×2桁」の演算です。
そして、九九で対応できない、という状況に陥ります。
しかし!
やっぱりベースは九九。
どこかの国の特異な教育を受けているのでない限り、九九をベースに考えていくのが早道と言えます。
そして・・・
いわゆる「さくらんぼ算」が、たいへん効果的です!
さくらんぼ算とは、数字を2つのパーツに分けていく手法です。
たとえば、「7」を 5と2 に分けて
12×7 = 12×5 + 12×2
にする、という感じです。これを使えば
12×7 = 60 + 24 = 84
となります。
大人は経験値があるため、筆算を頭の中で想像できたりして、12×7 では「ありがたみ」が薄いかもしれませんが、次のような計算ではいかがですか?
13×23=?
ま、簡単ですよね(笑)
そうなんです、こういうところで、工夫するとスピードが出るんです!
「23 を 20 と 3 に分ける」なら、流れはこうです。
13×23 = 13×20 + 12×3
= 260 + 39
= 299
なんとまあ…
結局のところ、筆算を1段ずつやっているにすぎない
さくらんぼ算に否定的な意見があるようですが、それは「筆算を知らない子ども」を作りたくないからかもしれません。
しかし、上記の方法だと、手法としては「2ケタ×2ケタ」の筆算を平らにしてやっているにすぎません。
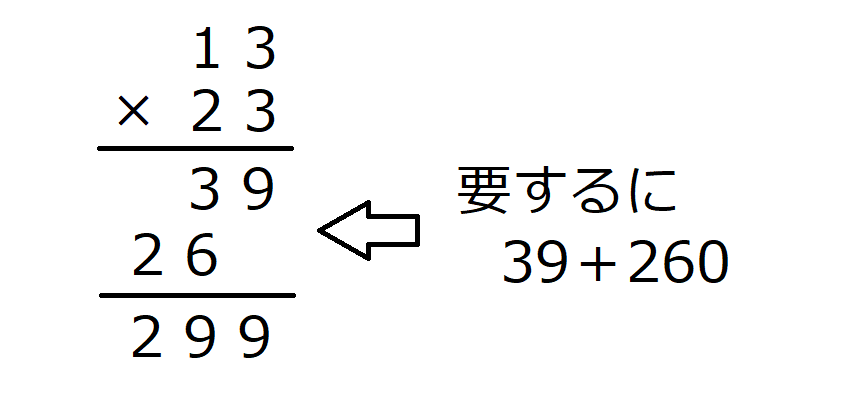
実際に計算が求められるときには、この方法で「2ケタ×2ケタ」をすることはたいへん効果的です。
答えを出す時だけでなく
合っているかどうかの「たしかめ」
を行う時にも活用しましょう。
そして、分解する手法のいいところは…
別に「十の位」と「一の位」で区切る必要はない
筆算では、片方の2ケタを、強制的に「十の位」と「一の位」に分けます。
しかし、自分にとって計算しやすい分け方にカスタマイズできれば、やりくり上手になります!
例えば…
12×14=?
多くの人が知っているかけ算に「平方」というものがあります。次のようなものは、有名でよく知られています。
1×1=1 2×2=4 3×3=9 4×4=16
5×5=25 6×6=36 7×7=49 8×8=64
9×9=81 10×10=100 11×11=121 12×12=144
ここまでは、知っておいたほうがいいと思います!
そして、これが利用できます!
ということで…
12×14 = 12×12 + 12×2
= 144 + 24
= 168
12×12 を導入する方法だってありますもんね!
筆算っぽく説明すると、以下のような感じです。

今であれば、小学生がこのように解いて提出しても「居残り」を回避できるかもしれません。学校現場もかなり柔軟になってきているので、現代であれば、先生から褒められるかもしれません。
筆算をする計算力があるなら、計算を工夫する力もあるはずです。原理を考える人になり、複数のアプローチができる人を目指して、ぜひチャレンジしてみましょう!
それでは、本日の講座はここまでです。
最後までお読みいただき、ありがとうございました!
この講座の様子がお分かりいただけたでしょうか。
この講座は、新しい考え方を入れる講座です。頭の中をアップデートするため、ぜひ継続的にお読みいただければ幸いです。
講座には、こちらからご参加ください!▼

https://college.coeteco.jp/s/shigumakaitacksmath
STORES でも同じ内容をご購入いただけます。 STORESはこちら ↓
勉強方法はみんなさまざま… 頭の使い方もみんなさまざまです。
ぜひ、皆さまの「選び」の参考になれば幸いです。短時間で良い勉強ができることを願っております!
こちらの記事もぜひご覧ください。
この記事が気に入ったらサポートをしてみませんか?
