＜学習シリーズ＞線形モデル編：重回帰分析

１．概要

１－１．緒言

　本記事は”学習シリーズ”として自分の勉強備忘録用になります。

　過去の記事で機械学習・AIの記事を多数作成しましたが、シンプルな線形モデルは外挿が比較的得意のためいろんな分野で使用されます。
　前回記事に引き続き、本記事では重回帰分析を紹介します。

１－２．用語・記号の説明（全般）

　本記事で使用する用語および記号は下記の通りです。

　１－２－１．用語一覧

●回帰 (regression)：実数値を予測する問題
●分類 (classification)：カテゴリ（離散値）を予測する問題
●教師あり学習 (supervised learning)：機械学習でデータセットに対して正解値（ラベル）がある学習方法
●教師なし学習 (unsupervised learning)：機械学習でデータセットに対して正解値（ラベル）が無い学習方法
●予測値 (predicted value)：関数で計算された出力変数y（用語は下記参照）
●目標値 (target value)：予測値がとるべき値（教師あり学習の正解値）
●目的関数 (objective function)：機械学習において性能の良さの指標を表す関数です。一般的には”予想値と目標値の差異”から作成される関数であり、この関数を最小化することでよいモデルと判断します。
●多重共線性（multicollinearity）：多変量解析（重回帰分析など）において、いくつかの説明変数間で線形関係（強い相関関係）があると共線性といい、共線性が複数認められる場合は多重共線性があると言います。
●二乗和誤差 (sum-of-squares error)：正解値$${y}$$と予測値$${\hat{y}}$$の差の２乗$${(y-\hat{y})^2}$$です。これをモデルと正解値の誤差とも呼びます。
●最小二乗法：二乗和誤差を最小化することでモデルの当てはまりを最適化する手法です。

　１－２－２．記号一覧

●$${f()}$$：$${y=f(x)}$$におけるf()であり関数と呼びます。中身は入力変数xを処理して新しい出力変数yを生成する計算式です。
●$${x}$$：$${y=f(x)}$$におけるxです。複数は下記の通り複数あります。
　名称１：説明変数（Explanatory variable）
　名称２：独立変数（Independent variable）
　名称３：外生変数（Exogenous variable）
　名称４：入力変数（Input variable）
　名称５：入力値（Input value）
●$${y}$$：$${y=f(x)}$$におけるyです。複数は下記の通り複数あります。
　名称１：目的変数（Response variable）
　名称２：従属変数（Dependent variable）
　名称３：被説明変数（Explained variable）
　名称４：内生変数（endogenous variable）
　名称５：出力変数（Output variable）
　名称６：予測値/推論値（prediction value）
●$${w_i}$$(weight)：重み（単回帰の場合は傾きとも言う）
●$${b}$$(bias)：バイアス（単回帰の場合は切片とも言う）

　１－２－３．ベクトル・行列表記一覧

●M次元の縦ベクトル：$${{\bf x}}$$

$$
\begin{aligned}{\bf x}= \begin{bmatrix} x_{0} \\ x_{1}\\ x_{2} \\ \vdots \\ x_{M} \end{bmatrix} \\ \end{aligned}
$$

●M次元の横ベクトル(縦ベクトルの転置)：$${{\bf x}^{\rm T}}$$

$$
\begin{aligned}{\bf x}^{\rm T}= \begin{bmatrix} x_{0} & x_{1}& x_{2} & \dots & x_{M} \end{bmatrix} & \end{aligned}
$$

●N×M次元の行列(M次元をもつN個のデータ)：$${{\bf X}}$$

$$
\begin{aligned}
{\bf X} &
= \begin{bmatrix} x_{10} & x_{11} & x_{12} & \cdots & x_{1M} \\
x_{20} & x_{21} & x_{22} & \cdots & x_{2M} \\
x_{30} & x_{31} & x_{32} & \cdots & x_{3M} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\ x_{N0} & x_{N1} & x_{N2} & \cdots & x_{NM} \end{bmatrix}
\end{aligned}
=\begin{bmatrix} {\bf x}_1^{\rm T} \\ {\bf x}_2^{\rm T} \\  {\bf x}_3^{\rm T}\\ \vdots \\ {\bf x}_N^{\rm T} \end{bmatrix}
$$

１－３．サンプル用データ：Diabetes

　サンプルデータはScikit-learnのToy datasetsを使用します。今回は回帰(Regression)のため"diabetes"を使用しました。重回帰は多次元の変数を取得できますが、可視化しやすいよう特徴量として重要な"s5"と"bmi"の2つだけ抽出しました。

[IN]
# %matplotlib qt
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn import datasets


#データセットの読み込み
diabetes = datasets.load_diabetes()
data, target = diabetes.data, diabetes.target
df_data = pd.DataFrame(data, columns=diabetes.feature_names)
df_data = df_data[['s5', 'bmi']] #単回帰として使用するため1次元のみ抽出
print(type(df_data), df_data.shape, type(target), target.shape)


#データの可視化:3次元プロット
plt.rcParams['font.size'] = 14
fig = plt.figure(figsize=(10, 10), facecolor='w')
ax = Axes3D(fig)
ax.scatter(df_data['s5'], df_data['bmi'], target, c='b', marker='o', s=50)
ax.set(xlabel='s5', ylabel='bmi', zlabel='target')
plt.grid()
plt.show()

[OUT]
<class 'pandas.core.frame.DataFrame'> (442, 1) <class 'numpy.ndarray'> (442,)

7.1. Toy datasets

【補足：３Dプロットのinteractive化】
　３DプロットをJupyter内で触れるように"ipympl"をインストールしてコード内に"%matplotlib qt"を追加しました。

[Terminal]
pip install ipympl

Make 3D interactive Matplotlib plot in Jupyter Notebook - GeeksforGeeks

２．重回帰モデル

２－１．重回帰モデルとは

　単回帰分析が「1 つの入力変数$${x}$$から 1 つの出力変数$${y}$$を出力するモデル」に対して、重回帰分析は「複数の入力変数$${x}$$から 1 つの出力変数$${y}$$を出力するモデル」です。よって単回帰の多次元拡張版モデルのようなものになります。
　単回帰と同じで、重回帰はモデルの解釈性が非常に高く外挿での動作も理解しやすいモデルとなります。

●$${x}$$：入力変数
●$${y}$$：出力変数
●$${w}$$：重み(単回帰での傾き$${a}$$と同等）
●$${b}$$：バイアス（単回帰での切片と同等）

$$
単回帰：y = wx+b
$$

$$
重回帰：y = w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{M}x_{M} + b=\sum_{m=1}^{M} w_{m} x_{m} + b
$$

　M次元の入力変数$${x}$$に$${x_0=1}$$を追加してM+1次元とし、同様にM次元の重み$${w}$$に$${w_0=b}$$を追加すると下記へ変換できます。

$$
\begin{aligned} y &
= w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{M}x_{M} + b \\ &
= w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{M}x_{M} + w_{0}x_{0} \\ &
= w_{0}x_{0} + w_{1}x_{1} + \cdots + w_{M}x_{M} \\ &
= \sum_{m=0}^M w_{m} x_{m} \end{aligned}
$$

２－２．重回帰を行列に変換

　重回帰は多次元のためベクトル・行列で表され、直接解法も行列で計算するため行列式で表現する方が便利となります。
　重回帰を重み$${\bf w}$$と説明変数$${\bf x}$$のベクトルの内積で表現するることができます。なお注意点は下記の通りです。

• バイアス$${b}$$は$${x_0=1}$$, $${w_0=b}$$より$${w_0x_0=b}$$で存在

• バイアス$${b}$$を含むため$${\bf w}$$, $${\bf x}$$共にM+1次元

• ベクトル同士の内積を計算するために、重み$${\bf w}$$は転置

【データ数が1個(1行の行列)：1×(M+1)行列】

$$
\begin{aligned} y = w_{0}x_{0} + w_{1}x_{1} + \cdots + w_{M}x_{M} = \begin{bmatrix} w_{0} & w_{1} & \cdots & w_{M} \end{bmatrix} \begin{bmatrix} x_{0} \\ x_{1} \\ \vdots \\ x_{M} \end{bmatrix} = {\bf w}^{\rm T}{\bf x}
\end{aligned}
$$

【データ数がN個(N行の行列)：(N×(M+1)行列)】

$$
\begin{aligned}{\bf y}&
=\begin{bmatrix} y_1 \\ y_2 \\y_3 \\ \vdots \\ y_N \end{bmatrix}
=\begin{bmatrix}{\bf x}_1^{\rm T}{\bf w} \\{\bf x}_2^{\rm T}{\bf w} \\{\bf x}_3^{\rm T}{\bf w} \\\vdots \\{\bf x}_N^{\rm T}{\bf w}\end{bmatrix}
= \begin{bmatrix}w_{10}x_{10} + w_{11}x_{11} + w_{12}x_{12} + \cdots + w_{1M}x_{1M} \\w_{20}x_{20} + w_{21}x_{21} + w_{22}x_{22} + \cdots + w_{2M}x_{2M} \\  w_{30}x_{30} + w_{31}x_{31} + w_{32}x_{32} + \cdots + w_{3M}x_{3M} \\
\vdots
\\w_{N0}x_{N0} + w_{N1}x_{N1} + w_{N2}x_{N2} + \cdots + w_{NM}x_{NM}\end{bmatrix}\end{aligned}
$$

$$
=\begin{bmatrix}x_{10} & x_{11} & x_{12} & \cdots & x_{1M} \\
x_{20} & x_{21} & x_{22} & \cdots & x_{2M} \\
x_{30} & x_{31} & x_{32} & \cdots & x_{3M} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{N0} & x_{N1} & x_{N2} & \cdots & x_{NM}\end{bmatrix}
\begin{bmatrix}w_{0} \\w_{1} \\w_{2}  \\\vdots \\w_{M}\end{bmatrix}
= {\bf X}{\bf w}
$$

３．直接解法の計算

　深層学習（ディープラーニング）などではモデルの学習時に誤差逆伝搬を使用して学習させますが、重回帰の重みとバイアスは直接計算可能です。
　最小二乗法を用いて誤差が最小になるパラメータを直接計算してみます。

３－１．結論

　結果は下記の通りであり「Normal Equation（正規方程式）」と呼ばれるものになります。

$$
\begin{aligned} {\bf w}
=\begin{bmatrix}w_{0} \\w_{1} \\w_{2}  \\\vdots \\w_{M}\end{bmatrix}
=\begin{bmatrix}b \\w_{1} \\w_{2}  \\\vdots \\w_{M}\end{bmatrix}
= ({\bf X}^{\rm T}{\bf X})^{-1}{\bf X}^{\rm T}{\bf t} \end{aligned}
$$

３－２．記号の定義一覧

　各種変数を示します。参考として統計用語は下記記事をご確認ください。

●データ数N, M+1次元(バイアス項含む)の説明変数:$${{\bf X \in \mathbb{R}^{N \times (M+1)}}}$$

$$
\begin{aligned}
{\bf X} &
= \begin{bmatrix} x_{10} & x_{11} & x_{12} & \cdots & x_{1M} \\
x_{20} & x_{21} & x_{22} & \cdots & x_{2M} \\
x_{30} & x_{31} & x_{32} & \cdots & x_{3M} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\ x_{N0} & x_{N1} & x_{N2} & \cdots & x_{NM} \end{bmatrix}
\end{aligned}
$$

●データ数Nの出力変数（推論値）:$${{\bf y}}$$

$$
\begin{aligned}{\bf y}&
=\begin{bmatrix} y_1 \\ y_2 \\y_3 \\ \vdots \\ y_N \end{bmatrix} \end{aligned}
$$

●バイアスを含むM+1次元の重みベクトル:$${{\bf w \in \mathbb{R}^{M+1}}}$$

$$
\begin{aligned} {\bf w}
=\begin{bmatrix}b \\w_{1} \\w_{2}  \\\vdots \\w_{M}\end{bmatrix}
=\begin{bmatrix}w_{0} \\w_{1} \\w_{2}  \\\vdots \\w_{M}\end{bmatrix}
\end{aligned}
$$

●データ数Nの正解値（ラベルデータ）:$${{\bf t}}$$

$$
\begin{aligned}{\bf t}&=\begin{bmatrix} t_1 \\ t_2 \\t_3 \\ \vdots \\ t_N \end{bmatrix} \end{aligned}
$$

●最小二乗誤差関数：$${Loss}$$

$$
Loss = \sum_{n=1}^N (t_n - y_n)^2= (t_1 - y_1)^2 + (t_2 - y_2)^2 + \cdots + (t_N - y_N)^2
$$

　ベクトルに変換すると

$$
\begin{aligned} Loss &
= (t_1 - y_1)^2 + (t_2 - y_2)^2 + \cdots + (t_N - y_N)^2 \\ &
= \begin{bmatrix} t_1 - y_1 & t_2 - y_2 & \cdots & t_N - y_N \end{bmatrix} \begin{bmatrix} t_1 - y_1 \\ t_2 - y_2 \\ \vdots \\ t_N - y_N \end{bmatrix} \\ &
= ({\bf t} - {\bf y})^{\rm T}({\bf t} - {\bf y}) \end{aligned}
$$

３－３．重みとバイアスの導出

　３－３－１：二乗和誤差の計算

　まずは最小化したい二乗和誤差Lossを計算します。計算には下記転置の公式を使用しました。

【転置の公式】
●$${({\bf A}{\bf B})^{\rm T} = {\bf B}^{\rm T}{\bf A}^{\rm T}}$$
●$${({\bf A}{\bf B}{\bf C})^{\rm T} = {\bf C}^{\rm T}{\bf B}^{\rm T}{\bf A}^{\rm T}}$$

$$
\begin{aligned} Loss &
= ({\bf t} - {\bf y})^{\rm T} ({\bf t} - {\bf y}) \\ &= ({\bf t} - {\bf X}{\bf w})^{\rm T} ({\bf t} - {\bf X}{\bf w}) \\ &= \{ {\bf t}^{\rm T} - ({\bf X}{\bf w})^{\rm T} \} ({\bf t} - {\bf X}{\bf w}) \\ &
= ({\bf t}^{\rm T} - {\bf w}^{\rm T}{\bf X}^{\rm T}) ({\bf t} - {\bf X}{\bf w})　\\ &
={\bf t}^{\rm T}{\bf t} - {\bf t}^{\rm T}{\bf X}{\bf w} - {\bf w}^{\rm T}{\bf X}^{\rm T}{\bf t} + {\bf w}^{\rm T}{\bf X}^{\rm T}{\bf X}{\bf w}
\end{aligned}
$$

　$${\bf w \in \mathbb{R}^{M+1}}$$, $${\bf X \in \mathbb{R}^{N \times (M+1)}}$$, $${\bf t \in \mathbb{R}^{N }}$$より$${({\bf t}^{\rm T}{\bf X}{\bf w})^{\rm T}}$$の内積を計算すると値はスカラーとなります。

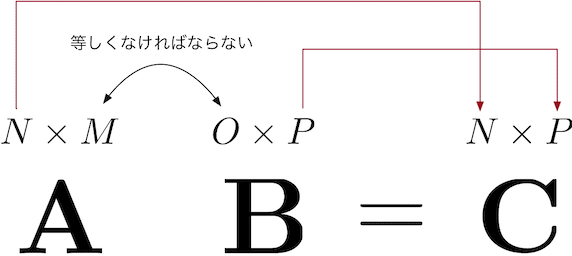
$$
({\bf t}^{\rm T}{\bf X}{\bf w})^{\rm T} =\mathbb{R}^{1 \times N }\mathbb{R}^{N \times M+1}\mathbb{R}^{(M+1) \times 1 }= \mathbb{R}^{1×1}
$$

　スカラーは転置しても形状変化がないため値も変化ありません。また転置の公式を適用すると下記の通りとなります。

$$
\bf t^{\rm T}{\bf X}{\bf w}
=({\bf t}^{\rm T}{\bf X}{\bf w})^{\rm T}
= {\bf w}^{\rm T} {\bf X}^{\rm T} {\bf t}
$$

　上式をLossの計算結果に代入すると下記が算出できます。

$$
\begin{aligned} Loss &
={\bf t}^{\rm T}{\bf t} - 2{\bf t}^{\rm T}{\bf X}{\bf w}+ {\bf w}^{\rm T}{\bf X}^{\rm T}{\bf X}{\bf w}
\end{aligned}
$$

　３－３－２．ｗでの偏微分を計算

　二乗和誤差Lossを$${{\bf w }}$$でまとめると下記の通りです。

$$
\begin{aligned} Loss &
= {\bf t}^{\rm T}{\bf t} - 2{\bf t}^{\rm T}{\bf X}{\bf w} + {\bf w}^{\rm T}{\bf X}^{\rm T}{\bf X}{\bf w} \\ &
= {\bf t}^{\rm T}{\bf t} - 2({\bf X}^{\rm T}{\bf t})^{\rm T} {\bf w} + {\bf w}^{\rm T}{\bf X}^{\rm T}{\bf X}{\bf w} \\ &
= c + {\bf b}^{\rm T}{\bf w} + {\bf w}^{\rm T}{\bf A}{\bf w} \end{aligned}
$$

　各定数$${\bf A}$$,  $${\bf B}$$,  $${c}$$はそれぞれ下記の通りです。

$$
\begin{aligned}
{\bf A} &= {\bf X}^{\rm T}{\bf X} \\ 
{\bf b} &= -2 {\bf X}^{\rm T}{\bf t} \\
c &= {\bf t}^{\rm T}{\bf t}
\end{aligned}
$$

　Lossのwでで偏微分の式は下記の通りです。

$$
\begin{aligned}
\frac {\partial}{\partial {\bf w}} Loss
=\begin{bmatrix} \frac {\partial}{\partial w_0} Loss \\
\frac {\partial}{\partial w_1} Loss \\ \vdots \\
\frac {\partial}{\partial w_M} Loss \\ \end{bmatrix} &
= \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \\ \end{bmatrix} \\
\end{aligned}
$$

　下記変形式を元にLossの偏微分を変換すると下記の通りとなります。

【変形式】

$$
\begin{aligned} \frac{\partial}{\partial {\bf x}} \left( {\bf a}^{\rm T}{\bf x} \right) &= \begin{bmatrix} \frac{\partial}{\partial x_1} \left( a_1x_1 + a_2x_2 \cdots + a_nx_n\right) & \frac{\partial}{\partial x_2} \left( a_1x_1 + a_2x_2 \cdots + a_nx_n\right) & \cdots & \frac{\partial}{\partial x_n} \left( a_1x_1 + a_2x_2 \cdots + a_nx_n\right) \end{bmatrix} \ &= \begin{bmatrix} a_1 & a_2 & \cdots & a_n \end{bmatrix} = {\bf a}^{\rm T} \end{aligned}
$$

$$
\begin{aligned}
\frac {\partial}{\partial {\bf w}} Loss
&= \frac{\partial}{\partial {\bf w}} (c + {\bf b}^{\rm T}{\bf w} + {\bf w}^{\rm T}{\bf A}{\bf w}) \\ &=\frac{\partial}{\partial {\bf w}} (c) + \frac{\partial}{\partial {\bf w}} ({\bf b}^{\rm T}{\bf w}) + \frac{\partial}{\partial {\bf w}} ({\bf w}^{\rm T}{\bf A}{\bf w}) \\ &
={\bf 0} + {\bf b}^{\rm T} + {\bf w}^{\rm T}({\bf A} + {\bf A}^{\rm T}) \end{aligned}
$$

　誤差の最小は傾き$${\frac {\partial}{\partial {\bf w}} Loss=0}$$より、①$${\bf A= {\bf X}^{\rm T}{\bf X}}$$,  $${{\bf b} = -2 {\bf X}^{\rm T}{\bf t} }$$を展開、②両辺を転置して$${\bf w^T}$$の転置を戻すと下記の通りです。

$$
\begin{aligned}
-2({\bf X}^{\rm T}{\bf t})^{\rm T} + {\bf w}^{\rm T} \{ {\bf X}^{\rm T}{\bf X} + ({\bf X}^{\rm T}{\bf X})^{\rm T} \} &= {\bf 0} \\
-2{\bf t}^{\rm T}{\bf X} + 2{\bf w}^{\rm T}{\bf X}^{\rm T}{\bf X} &= {\bf 0} \\
{\bf w}^{\rm T}{\bf X}^{\rm T}{\bf X}& = {\bf t}^{\rm T}{\bf X} \\
({\bf w}^{\rm T}{\bf X}^{\rm T}{\bf X}) ^{\rm T} & = ({\bf t}^{\rm T}{\bf X}) ^{\rm T} \\ {\bf X}^{\rm T}{\bf X}{\bf w} & = {\bf X}^{\rm T}{\bf t} \\
\end{aligned}
$$

　最後に$${{\bf X}^{\rm T}{\bf X}}$$に逆行列が存在すると仮定して、両辺に左側から$${({\bf X}^{\rm T}{\bf X})^{-1}}$$をかけると重みwの解が求まります。この式を正規方程式 (normal equation) と呼びます。

$$
\begin{aligned}
({\bf X}^{\rm T}{\bf X})^{-1} {\bf X}^{\rm T}{\bf X} {\bf w} &= ({\bf X}^{\rm T}{\bf X})^{-1} {\bf X}^{\rm T}{\bf t} \\ {\bf I}{\bf w} &= ({\bf X}^{\rm T}{\bf X})^{-1} {\bf X}^{\rm T}{\bf t} \\ {\bf w} &= ({\bf X}^{\rm T}{\bf X})^{-1}{\bf X}^{\rm T}{\bf t}
\end{aligned}
$$

４．単回帰モデルの実装：スクラッチ編

　動作を理解するためにPythonのライブラリを使用せずスクラッチで計算します。目視で確認できるようにデータ数を1桁に調整しました。

[IN]
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import japanize_matplotlib
import seaborn as sns
import os

from sklearn import datasets
from sklearn.model_selection import train_test_split

#データセットの読み込み
diabetes = datasets.load_diabetes()
data, target = diabetes.data, diabetes.target
df_data = pd.DataFrame(data, columns=diabetes.feature_names)
df_data = df_data[['s5', 'bmi']] #単回帰として使用するため1次元のみ抽出

#データの分割：参照用のデータ数を少なくする
x_train, x_test, y_train, y_test = train_test_split(df_data, target, test_size=0.98, random_state=0)
print(f'x_train: {x_train.shape}, x_test: {x_test.shape}, y_train: {y_train.shape}, y_test: {y_test.shape}')
print(f'x_train: {type(x_train)}, x_test: {type(x_test)}, y_train: {type(y_train)}, y_test: {type(y_test)}')

#Excel処理用としてデータを結合／出力
_data = np.concatenate([x_train, y_train.reshape(-1, 1)], axis=1)
df_dataset = pd.DataFrame(_data, columns=['s5', 'bmi', 'target'])
display(df_dataset)

#Excelファイルの出力
if not os.path.exists('data'):
    os.mkdir('data') #ディレクトリが存在しない場合のみ作成
    print(f'ディレクトリを作成しました: {os.path.abspath("data")}')

df_dataset.to_excel('data/dataset_diabetes2dim.xlsx', index=False)

#データの可視化:3次元プロット
plt.rcParams['font.size'] = 14
fig = plt.figure(figsize=(10, 10), facecolor='w')
ax = Axes3D(fig)
ax.scatter(df_dataset['s5'].values, df_dataset['bmi'].values, y_train, c='b', marker='o', s=50)
ax.set(xlabel='s5', ylabel='bmi', zlabel='target')
plt.grid()
plt.show()

[OUT]
x_train: (8, 2), x_test: (434, 2), y_train: (8,), y_test: (434,)
x_train: <class 'pandas.core.frame.DataFrame'>, x_test: <class 'pandas.core.frame.DataFrame'>, y_train: <class 'numpy.ndarray'>, y_test: <class 'numpy.ndarray'>

	s5	        bmi	        target
0	0.014823	0.005650	311.0
1	0.007837	0.025051	122.0
2	0.084495	0.098342	243.0
3	0.129019	-0.007284	248.0
4	-0.029528	-0.030996	91.0
5	0.079121	-0.021295	281.0
6	-0.018118	-0.073030	142.0
7	0.073410	0.071397	295.0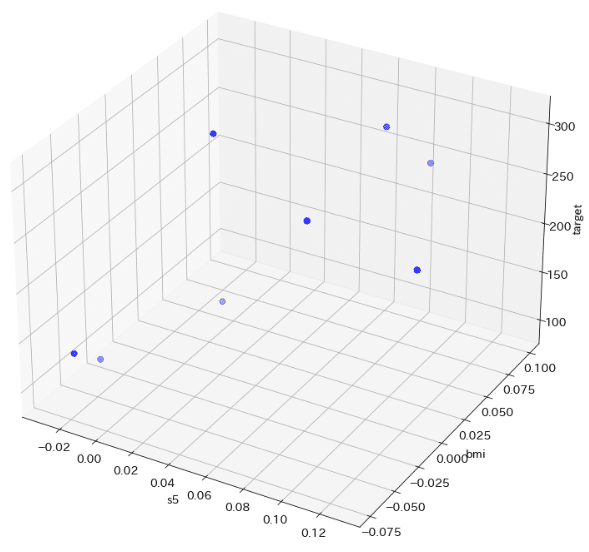

４－１．Pythonで計算：Numpy

　結論として、求める重み$${\bf w}$$の計算式は下記の通りです。

$$
\begin{aligned} {\bf w}
=\begin{bmatrix}b \\w_{1} \\w_{2}  \\\vdots \\w_{M}\end{bmatrix}
=\begin{bmatrix}w_{0} \\w_{1} \\w_{2}  \\\vdots \\w_{M}\end{bmatrix}
= ({\bf X}^{\rm T}{\bf X})^{-1}{\bf X}^{\rm T}{\bf t} \end{aligned}
$$

　説明変数$${\bf X}$$と目的変数$${\bf t}$$は下記を使用します。

$$
X = \begin{bmatrix}0.0148 & 0.0056 \\0.0078 & 0.0251 \\0.0845 & 0.0983 \\0.1290 & -0.0073 \\-0.0295 & -0.0310 \\0.0791 & -0.0213 \\-0.0181 & -0.0730 \\0.0734 & 0.0714 \end{bmatrix}
$$

$$
t = \begin{bmatrix}311 \\122 \\243 \\248 \\91 \\281 \\142 \\295 \end{bmatrix}
$$

　Xにはバイアス項として1列目に1を追加します。

$$
X = \begin{bmatrix}1 & 0.0148 & 0.0056 \\1 & 0.0078 & 0.0251 \\1 & 0.0845 & 0.0983 \\1 & 0.1290 & -0.0073 \\1 & -0.0295 & -0.0310 \\1 & 0.0791 & -0.0213 \\1 & -0.0181 & -0.0730 \\1 & 0.0734 & 0.0714
\end{bmatrix}
$$

　順序通りに計算すると下記解が得られます。

$$
\begin{aligned} {\bf w}
= ({\bf X}^{\rm T}{\bf X})^{-1}{\bf X}^{\rm T}{\bf t} \end{aligned}
=\begin{bmatrix}b \\w_{1} \\w_{2} \end{bmatrix}
=\begin{bmatrix}w_{0} \\w_{1} \\w_{2} \end{bmatrix}
=\begin{bmatrix}175.4 \\926.9 \\199.3 \end{bmatrix}
$$

[IN]
X = df_dataset[['s5', 'bmi']].values
t = df_dataset['target'].values
bias = np.ones((X.shape[0], 1)) #バイアス項用に1のベクトル作成

X = np.concatenate([bias, X], axis=1) #バイアス項をXに結合
X_T = X.T #Xの転置行列
X_TX = np.dot(X_T, X) #X_TとXの行列積
X_TX_inv = np.linalg.inv(X_TX) #X_TXの逆行列
X_TX_inv_X_T = np.dot(X_TX_inv, X_T) #X_TX_invとX_Tの行列積
weights = np.dot(X_TX_inv_X_T, t) #X_TX_inv_X_Tとtの行列積

print('説明変数X')
display(X)
print('\nXの転置行列X_T')
display(X_T)
print('\nX_TとXの行列積X_TX')
display(X_TX)
print('\nX_TXの逆行列X_TX_inv')
display(X_TX_inv)
print('\nX_TX_invとX_Tの行列積X_TX_inv_X_T')
display(X_TX_inv_X_T)
print('\nweights')
display(weights.reshape(-1, 1))

[OUT]
説明変数X
array([[ 1.   ,  0.015,  0.006],
       [ 1.   ,  0.008,  0.025],
       [ 1.   ,  0.084,  0.098],
       [ 1.   ,  0.129, -0.007],
       [ 1.   , -0.03 , -0.031],
       [ 1.   ,  0.079, -0.021],
       [ 1.   , -0.018, -0.073],
       [ 1.   ,  0.073,  0.071]])

Xの転置行列X_T
array([[ 1.   ,  1.   ,  1.   ,  1.   ,  1.   ,  1.   ,  1.   ,  1.   ],
       [ 0.015,  0.008,  0.084,  0.129, -0.03 ,  0.079, -0.018,  0.073],
       [ 0.006,  0.025,  0.098, -0.007, -0.031, -0.021, -0.073,  0.071]])

X_TとXの行列積X_TX
array([[8.   , 0.341, 0.068],
       [0.341, 0.037, 0.013],
       [0.068, 0.013, 0.022]])

X_TXの逆行列X_TX_inv
array([[  0.214,  -2.234,   0.697],
       [ -2.234,  58.028, -28.279],
       [  0.697, -28.279,  59.963]])

X_TX_invとX_Tの行列積X_TX_inv_X_T
array([[ 0.185,  0.214,  0.094, -0.079,  0.259,  0.023,  0.204,  0.1  ],
       [-1.534, -2.488, -0.112,  5.459, -3.071,  2.959, -1.22 ,  0.007],
       [ 0.617,  1.978,  4.205, -3.388, -0.326, -2.817, -3.17 ,  2.902]])

weights
array([[175.421],
       [926.852],
       [199.317]])

４－２．Excelで計算１：フルスクラッチ

　重回帰をExcelを用いてスクラッチで計算します。転置や内積の関数は下記記事をご確認ください。フルスクラッチで計算すると結構手間なので通常は次節で紹介する分析ツールを使用します。

$$
\begin{aligned} {\bf w}
=\begin{bmatrix}b \\w_{1} \\w_{2}  \\\vdots \\w_{M}\end{bmatrix}
=\begin{bmatrix}w_{0} \\w_{1} \\w_{2}  \\\vdots \\w_{M}\end{bmatrix}
= ({\bf X}^{\rm T}{\bf X})^{-1}{\bf X}^{\rm T}{\bf t} \end{aligned}
$$

４－３．Excelで計算２：データ分析(回帰分析)

　Excelには単回帰／重回帰分析を計算できるツールとして「データ分析」があります。「データ」タブの「データ分析」から「回帰分析」を選択して、ラベル名も含めて選択後に”ラベル”にチェックを入れます。

　新規シートが作成され出力結果が表示されます。係数の列に重みとバイアスが確認できます。

５．単回帰モデルの実装：ライブラリ編

　より簡単にモデルを作成するためにライブラリを使用します。

５－１．Scikit-learn：LinearRegression

　Scikit-learnを使用して重回帰を実装します。こちらは単回帰と同じく、重回帰は”LinearRegression”で実装できます。
　Scikit-learnのAPIはシンプルでありモデルは下記フローで実装できます。

1. 使用する機械学習モデルをインポート

2. モデルのインスタンス化

3. 学習：model.fit()

4. 学習後のパイパーパラメータ確認

5. 推論：model.predict()

[IN]
from sklearn.linear_model import LinearRegression

#単回帰モデルの実装
linear = LinearRegression() #インスタンス化
linear.fit(x_train, y_train) #学習
y_pred = linear.predict(x_test) #予測

print('Weights:', linear.coef_) #傾き
print('bias', linear.intercept_) #切片

[OUT]
Weights: [926.852 199.317]
bias 175.42095342718756

　出力も確認しました。下記の通り１次元単回帰モデルは直線で表現されますが２次元重回帰モデルは平面で表現されます。

[IN]
#データの可視化:3次元プロット
plt.rcParams['font.size'] = 14
fig = plt.figure(figsize=(10, 10), facecolor='w')
ax = Axes3D(fig)
 #生データをプロット ax.scatter(df_dataset['s5'].values, df_dataset['bmi'].values, y_train,
           label='data', c='b', marker='o', s=50)

 #重回帰の推論値を平面で表示 x_min, x_max = df_dataset['s5'].min(), df_dataset['s5'].max() #x1の最小値、最大値
y_min, y_max = df_dataset['bmi'].min(), df_dataset['bmi'].max() #x2の最小値、最大値
xs = np.linspace(x_min, x_max, 100)  #x1の最小値から最大値まで100等分 ys = np.linspace(y_min, y_max, 100)  #x2の最小値から最大値まで100等分 
X, Y = np.meshgrid(xs, ys)
Z = np.zeros((len(xs), len(ys)))
print(f'形状確認　X：{X.shape}, Y:{Y.shape}, Z:{Z.shape}')

for i in range(len(xs)):
    for j in range(len(ys)):
        Z[j,i] = linear.predict([[xs[i], ys[j]]])

ax.plot_surface(X, Y, Z, alpha=0.5, cmap='Reds')  #平面を表示 ax.contour(X, Y, Z, 10, colors='black', linewidths=0.5)  #等高線を表示 
ax.set(xlabel='s5', ylabel='bmi', zlabel='target')
plt.grid()
plt.show()

[OUT]
形状確認　X：(100, 100), Y:(100, 100), Z:(100, 100)

【コラム】
　３次元空間(x,y,z)に対して2次元（平面）で表現される空間、つまり元の空間(n次元)より1次元低い空間(n-1次元)を超平面と呼びます。
　重回帰では独立変数（説明変数）が２つの場合は”回帰平面”、３つ以上では”回帰超平面”と呼びます。

５－２．Pytorch：nn.Linear()

　Pytorchで重回帰も実装できますが、sklearnの方が楽のため今回は省略しました。

６．補足：ベクトル・行列式の変換

【ベクトルの内積の入れ替え：$${{\bf w}^{\rm T}{\bf x}= {\bf x}^{\rm T}{\bf w}}$$】

$$
\begin{aligned}
{\bf w}^{\rm T}{\bf x}= {\bf x}^{\rm T}{\bf w}
= w_{0}x_{0} + w_{1}x_{1} + \cdots + w_{N}x_{N}
= \begin{bmatrix} w_{0} \ w_{1}\ w_{2} \ \dots \ w_{n} \end{bmatrix}
\begin{bmatrix} x_{0} \\ x_{1}\\ x_{2} \\ \vdots \\ x_{n} \end{bmatrix} 
=\begin{bmatrix} x_{0} \ x_{1}\ x_{2} \ \dots \ x_{n} \end{bmatrix}
\begin{bmatrix} w_{0} \\ w_{1}\\ w_{2} \\ \vdots \\ w_{n} \end{bmatrix}
\end{aligned}
$$

【転置の公式】

$$
\begin{aligned} &\ \left( {\bf A}^{\rm T} \right)^{\rm T} = {\bf A} \\
& \ \left( {\bf A}{\bf B} \right)^{\rm T} = {\bf B}^{\rm T}{\bf A}^{\rm T}\\
&\ \left( {\bf A}{\bf B}{\bf C} \right)^{\rm T} = {\bf C}^{\rm T}{\bf B}^{\rm T}{\bf A}^{\rm T} \end{aligned}
$$

$$
\begin{aligned}
{\bf A} \in \mathbb{R}^{N \times M }&
= \begin{bmatrix} a_{10} & a_{11} & a_{12} & \cdots & a_{1M} \\ a_{20} & a_{21} & a_{22} & \cdots & a_{2M} \\a_{30} & a_{31} & a_{32} & \cdots & a_{3M} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{N0} & a_{N1} & a_{N2} & \cdots & a_{NM} \end{bmatrix}, 
{\bf B} &\in \mathbb{R}^{M \times O }
= \begin{bmatrix} b_{10} & b_{11} & b_{12} & \cdots & b_{1O} \\ b_{20} & b_{21} & b_{22} & \cdots & b_{2O} \\b_{30} & b_{31} & b_{32} & \cdots & b_{3O} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ b_{M0} & b_{M1} & b_{M2} & \cdots & b_{MO} \end{bmatrix}
\end{aligned}
$$

$$
\begin{aligned}
{\bf A}^{\rm T} \in \mathbb{R}^{M \times N }&
= \begin{bmatrix} a_{10} & a_{20} & a_{30} & \cdots & a_{N0} \\
a_{11} & a_{21} & a_{31} & \cdots & a_{N1} \\
a_{12} & a_{22} & a_{32} & \cdots & a_{N2} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
a_{1M} & a_{2M} & a_{3M} & \cdots & a_{NM} \end{bmatrix}
,
{\bf B}^{\rm T} \in \mathbb{R}^{O \times M }
= \begin{bmatrix} b_{10} & b_{20} & b_{30} & \cdots & b_{M0} \\
b_{11} & b_{21} & b_{31} & \cdots & b_{M1} \\
b_{12} & b_{22} & b_{32} & \cdots & b_{M2} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
b_{1O} & b_{2O} & b_{3O} & \cdots & b_{MO} \end{bmatrix}
\end{aligned}
$$

$$
\begin{aligned}
{\bf B}^{\rm T} {\bf A}^{\rm T} =
\begin{bmatrix} b_{10} & b_{20} & b_{30} & \cdots & b_{M0} \\
b_{11} & b_{21} & b_{31} & \cdots & b_{M1} \\
b_{12} & b_{22} & b_{32} & \cdots & b_{M2} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
b_{1O} & b_{2O} & b_{3O} &\cdots & b_{MO}  \end{bmatrix}
\begin{bmatrix} a_{10} & a_{20} & a_{30} & \cdots & a_{N0} \\
a_{11} & a_{21} & a_{31} & \cdots & a_{N1} \\
a_{12} & a_{22} & a_{32} & \cdots & a_{N2} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
a_{1M} & a_{2M} & a_{3M} & \cdots & a_{NM}
\end{bmatrix}
\end{aligned}
$$

【ベクトルの微分１：$${\frac{\partial}{\partial {\bf x}} \left( {\bf w}^{\rm T}{\bf x} \right) = {\bf w}^{\rm T}}$$】

$$
\begin{aligned}
\frac{\partial}{\partial {\bf x}} \left( {\bf w}^{\rm T}{\bf x} \right)
=\frac{\partial}{\partial {\bf x}}(w_{0}x_{0} + w_{1}x_{1} + \cdots + w_{N}x_{N})
=\frac{\partial}{\partial {\bf x}}\sum_{i=1}^{n}w_ix_i
\end{aligned}
$$

$$
\begin{aligned}
=\begin{bmatrix}
\frac{\partial}{\partial x_1} \left(\sum_{i=1}^{n}w_ix_i \right) &
\frac{\partial}{\partial x_2} \left(\sum_{i=1}^{n}w_ix_i \right) & \dots &
\frac{\partial}{\partial x_n} \left(\sum_{i=1}^{n}w_ix_i \right)
\end{bmatrix}
= \begin{bmatrix} w_{0} \ w_{1}\ w_{2} \ \dots \ w_{n} \end{bmatrix}
= {\bf w}^{\rm T}
\end{aligned}
$$

【ベクトルの微分２：$${\frac{\partial}{\partial {\bf x}} \left( {\bf x}^{\rm T}{\bf A}{\bf x} \right) = {\bf x}^{\rm T} \left( {\bf A} + {\bf A}^{\rm T} \right)}$$】

$$
\begin{aligned}
 {\bf x}^{\rm T}{\bf A}{\bf x}
&= \begin{bmatrix} x_1 & x_2 & \cdots & x_N \end{bmatrix}
\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1N} \\
a_{21} & a_{22} & \cdots & a_{2N} \\
\vdots & \vdots & \ddots & \vdots \\
a_{N1} & a_{N2} & \cdots & a_{NN} \end{bmatrix}
\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_N \end{bmatrix}
=\begin{bmatrix} \sum_{i=1}^{N}x_ia_{i1} & \sum_{i=1}^{N}x_ia_{i2} & \cdots & \sum_{i=1}^{N}x_ia_{iN} \end{bmatrix}
\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_N \end{bmatrix}
= \sum_{i=1}^{N} \sum_{j=1}^{N} a_{ij} x_i x_j
\end{aligned}
$$

$$
\begin{aligned}
\frac{\partial}{\partial {\bf x}} \left( {\bf x}^{\rm T}{\bf A}{\bf x} \right)
&= \frac{\partial}{\partial {\bf x}} \left( \sum_{i=1}^{N} \sum_{j=1}^{M} a_{ij} x_i x_j \right) \
&= \begin{bmatrix} \frac{\partial}{\partial x_1} & \frac{\partial}{\partial x_2} & \cdots & \frac{\partial}{\partial x_N} \end{bmatrix} \begin{bmatrix} \sum_{i=1}^{N} \sum_{j=1}^{N} a_{ij} x_i x_j \end{bmatrix} 
\end{aligned}
$$

$$
\begin{aligned}
= \begin{bmatrix} \sum_{j=1}^{N} a_{1j} x_j & \sum_{j=1}^{N} a_{2j} x_j & \cdots & \sum_{j=1}^{N} a_{Nj} x_j \end{bmatrix} 
\end{aligned}
$$

$$
\begin{aligned}
&= \begin{bmatrix} x_1 & x_2 & \cdots & x_N \end{bmatrix}
\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1N} \\
a_{21} & a_{22} & \cdots & a_{2N} \\
\vdots & \vdots & \ddots & \vdots \\
a_{N1} & a_{N2} & \cdots & a_{NN} \end{bmatrix} +
\begin{bmatrix} x_1 & x_2 & \cdots & x_N \end{bmatrix}
\begin{bmatrix} a_{11} & a_{21} & \cdots & a_{N1} \\
a_{12} & a_{22} & \cdots & a_{N2} \\
\vdots & \vdots & \ddots & \vdots \\
a_{1N} & a_{2N} & \cdots & a_{NN}
\end{bmatrix} \
&= {\bf x}^{\rm T} \left( {\bf A} + {\bf A}^{\rm T} \right)
\end{aligned}
$$

---

参考資料

Pythonライブラリ（機械学習・AI）｜KIYO｜note

勉強・メモ用マガジン｜KIYO｜note

チュートリアル — ディープラーニング入門：Chainer チュートリアル

今後の教材用

リッジ回帰とラッソ回帰の理論と実装を初めから丁寧に - Qiita

最短でリッジ回帰とラッソ回帰を説明（機械学習の学習 #3） - Qiita

線形回帰の過学習を抑えよう ～Ridge回帰とLasso回帰～ | Nature Insight ネイチャーインサイト株式会社

あとがき

　後でプロット追加と超平面の話を追加