夏休みとバウムクーヘンと積分と

はじめに

昨日、こんな記事を書いた。

バウムクーヘン分割の素晴らしさを知ってほしくて書いたのだが、書いているうちに、そもそも積分の素晴らしさから知ってほしくなってしまった。

そのため、バウムクーヘン分割を理解することを目標として、まずは積分の必要性と素晴らしさを語ろうと思う。

ここまでくると、さりげなく言うことは不可能なので、堂々と語り明かす。

積分とは「足し算」

積分を一言で表すと、足し算である。そう、小学校の算数でまずはじめに習う、あの足し算である。

”積”などと書いておきながら、掛け算ではない。インテグラルなどというかっこいい記号を使っておきながら、やっていることは足し算である。

積分が足し算であることは、次の体積の例で詳しく説明する。

体積の求め方

中学校の数学で、立体の体積の求め方を習った。

体積 = 底面積 × 高さ

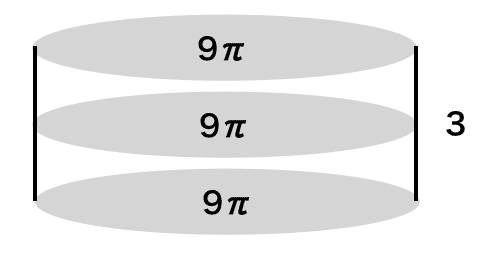
例えば底面積が9π、高さが3の円柱の体積は、27πである。

9π × 3 = 27π

体積がなぜこの公式で求められるか、考えたことがあるだろうか。

体積は、物体がその空間の中でどれくらいの大きさを占めるかを表したものである。そしてそれは、ものすごく薄い円の集合体として考えることができる。

つまり、9πの大きさのものすごく薄い円が、高さ3に渡って上に広がっているのが、この円柱である。誤解を恐れずもう少し簡単に言うと、9πの円が3つ積み重なったものである、と言ってもいい。

9π + 9π + 9π = 27π

三角錐の体積

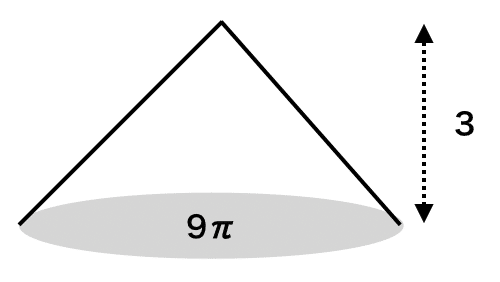
もう少し複雑な立体を考えてみよう。

これも中学校の数学で習ったものであるが、三角錐の体積の公式は、円柱とは公式が少し異なる。

三角錐の体積 = 底面積 × 高さ ÷ 3

なぜ、÷3が付いているのか、疑問に思ったことはあるだろうか。例え3という数字の意味がわからなくとも、底面積 × 高さだけで体積が求められないことは想像できる。（理由は下に記載する）

先ほど、「円柱の体積はものすごく薄い円の積み重ねである」と記載した。そしてその円柱における、1つ1つの円の大きさは9πだった。それが3つ集まって、27πとなった。

三角錐の体積も、基本的な考え方は同じである。ものすごく薄い円を考えて、それを積み重ねればよい。

...

と、ここで、あることに気がつく。

三角錐の場合、ものすごく薄い1つ1つの円の大きさが違っているではないか。

それもそのはず、三角錐は上に行くほど尖っている。したがって、円の大きさも上に行くほど小さくなってしまう。そのため、先ほどと同じように9π + 9π + 9πで体積を求めることはできない。（2つ目以降は9πにならないため）

このように、円の大きさが変わってしまう場合には、単純に9πを3回足すのでは体積を求めることができない。つまり単なる足し算は、通用しない。

そこで、もっと素晴らしい足し算が必要になる。

救世主、積分の登場。

積分と体積

三角錐では、ものすごく薄い円の大きさが上に行くにつれて小さくなってしまうため、体積を簡単に求めることができない。

ただ、どれくらいの割合で円の大きさが減るっていくのかがわかれば、計算によって体積を求められる気がしないだろうか。

ある値がどのくらいの割合で変化するのかを調べるとき、関数とそのグラフが役に立つ。そのため、まずはこの三角錐を座標平面上に置いてやる。

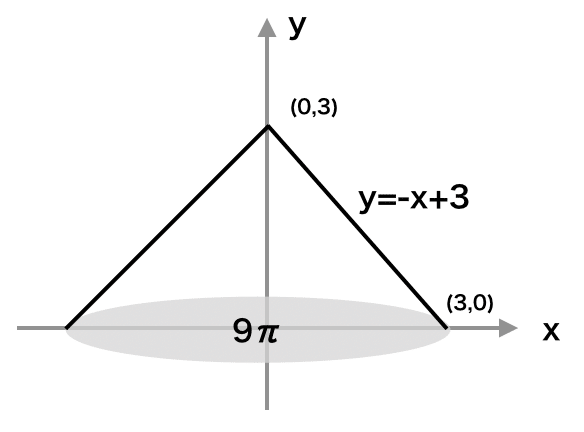
この直線は一次関数であり、式で表すことができる。

y = -x + 3

この時、先ほどと同様に、ものすごく薄い円を考えてみると、その円の半径はこの関数のx座標に相当する。そのため、あるyという高さにおける円の半径xが式変形によってわかる。

x = -y + 3

これは、上のy=の式を移項して、x=の形に直しただけである。

また、ある高さにおける円の半径がわかれば、円の面積も公式でわかる。

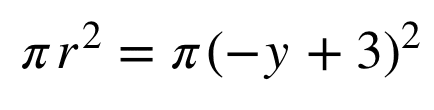
あとはこれを下から上まで足していく。”足す”というのはすなわち積分することである。

三角錐の公式を使ってみると、積分で求めた体積の値と一致することがわかる。

9π × 3 ÷ 3 = 9π

円柱の例で示した通り、体積はものすごく薄い面の積み重ね（足し算）である。積分によって算出した値が三角錐の体積と等しいということは、積分は面の積み重ねをする計算だということになる。

すなわち、積分は足し算なのである。

これでもピンとこない場合は、「区分求積」とググってもらうと、理解が深まるかもしれない。（さらに頭が混乱する場合もある）

満を辞して。

いよいよ、バウムクーヘン分割に再挑戦する。

前回の記事と同様、y=sinxを考える。この図形の回転体の体積を求めるために、まずはものすごく薄い円を考える。

ただし、今回のような図形の場合、底面こそ円となっているものの、それ以降は円ではなくドーナツ型の図形になる。

ドーナツ型の図形の面積は、大きい円から小さい円を引き算すればよい。

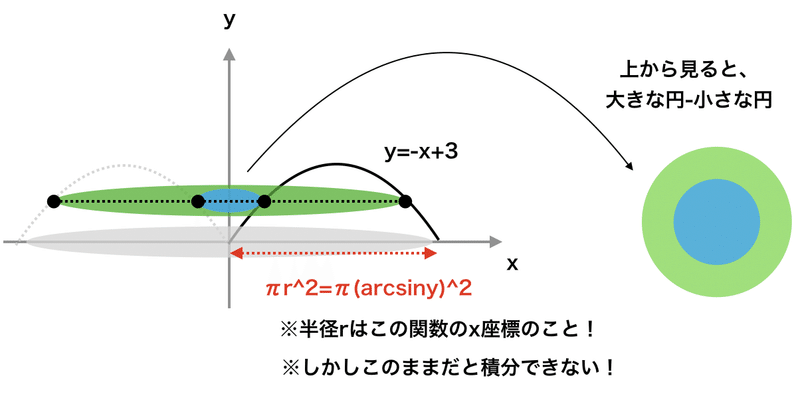
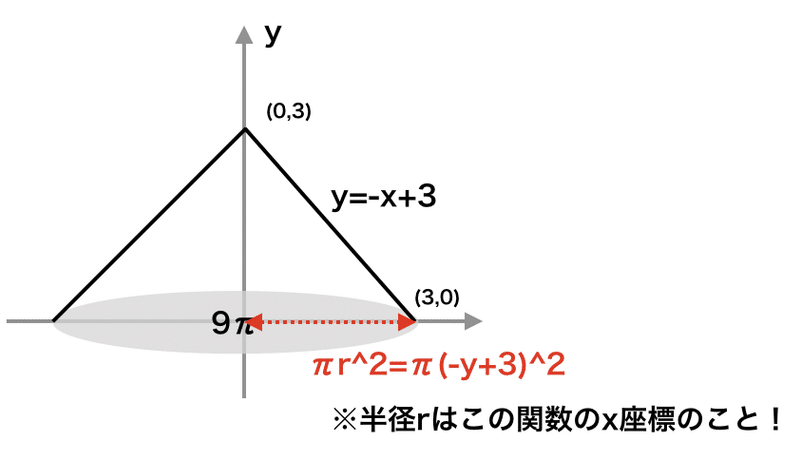
y = -x + 3をx = -y + 3とした三角錐の例と同じように、まずはあるyにおけるxを求めよう。

...

とここで、明らかにxを求める難易度が高いことに気がつく。何しろ、y=sinxである。x=の形に直そうとしても不可能で、せいぜい気晴らしにx=arcsinyと書くくらいが精一杯である。

どうすればいい？このまま、ものすごく薄いドーナツ型の図形の面積が求められず終わってしまうのか。

...

と、その時、急に懐かしい匂いがした。

ある暑い夏の日、セミの音がうるさく鳴り響いている。昨夜はあまり眠れなかった。決してストレスが原因というわけではない。楽しみだったのだ。

およそ自宅の徒歩15分圏内しか移動しない小学生の自分が、唯一遠出できるのがこの時期だ。そう、親の実家に帰省するのである。

たまに乗る最寄り駅までのバスはすぐに駅へと到着し、そこからいくつも電車を乗り継ぐ。するとすぐに、見慣れない風景が目に入る。これらが全て同じ世界の中にあるとは到底思えないほど、風景は代わる代わる視界を横切り、瞬時に全く別の世界が窓いっぱいに広がる。

そして最も楽しみなのが、この世界の乗り物とは思えないフォルムをした、新幹線である。この乗り物なら、未来へも飛び立てるかもしれない。そう思えるほどこの世界には似合わない形をしている。

とはいえ、乗り始めこそワクワクが収まらずにずっと外を眺めているものの、昨夜の睡眠不足によって眠気が襲う。親に起こされて到着した時には、これまた別世界かのような田園風景が広がっている。

電車を降りて改札を出ると、そこには見慣れた車が止まっている。

「おじいちゃんだ！」

車からゆっくり出てきたおじいちゃんは、開口一番にこう言う。

「よお。東京は暑いか？」

車に乗って数十分。家に着くと、おばあちゃんが首を長くして待っている。

「よく来たね。今お菓子持ってくるから、手を洗っちゃいなさい。」

そして机に運ばれる、お茶と、バウムクーヘン。

「なんだか不思議な模様だな。あれ？」

バウムクーヘンのぐるぐる模様を見ているうちに、気が遠くなり、別の世界に飛ばされている感覚が襲ってきた。

...

「そうだ。バウムクーヘン分割だ。」

ものすごく薄い図形の足し算は、何も底面でしか行ってはいけない訳ではない。回転体は、もちろん円（とドーナツ型の図形）の積み重ねと考えることもできるが、下から上へ積み上げるのではなく、左から右へ積み重ねることもできる。

つまり、ものすごく薄い円柱を左から右に積み重ねると、回転体が出来上がる。

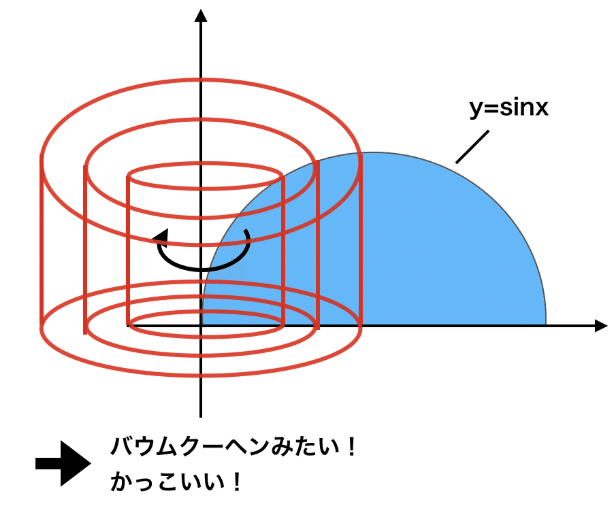
もし、イメージがつかないのなら、先ほどの三角錐の例を使ってもう一度体積を求めてみよう。

先ほどは、下から上に積み重ねた。しかしこれを左（x=0）から右に積み重ねようとすると、この関数のあるxにおけるyは、一次関数の式そのままy=-x+3となる。

この時、これを側面とする円柱を考えて、その側面積を求める。

2π × h = 2π × (-x+3)

そしてこれを積分する。

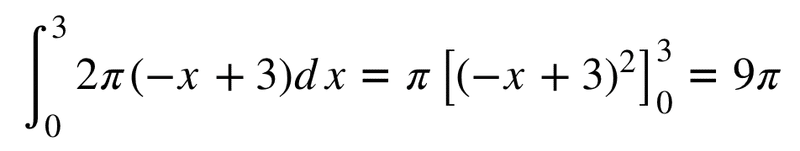
先ほどと同じ答えになった。

三角錐の場合のような単純な図形では、どちらの考え方でも難易度は変わらないが、関数の逆関数（つまりy=に対してx=の式）を求めるのが難しい時にはバウムクーヘン分割が有効である。

ここまで書いてようやく、バウムクーヘン分割が真に素晴らしいものであることを説明できた。

おわりに

おばあちゃんが出してくれるバウムクーヘンが、昔は苦手だった。あのパサパサした食感が、どうも受け付けなかった。

しかし、今ではあのパサパサ感を、逆に気に入っている。パサパサによって、自分自身が水分を渇望していることに自覚的になり、人間が人間であることを忘れて本能で生きる獣のようになれる気がする。

と、同時に、目が回るようなあの模様が、自分をどこか遠くの別の世界へ連れて行ってくれるような気がして、なおのこと自分が自分で無くなる感覚に襲われる。

現代は、”考える”ことが多すぎる。「〜するべき」があまりに蔓延っていて、何をしたらよいかわからなくなる時がある。

バウムクーヘンは、それらを忘れさせてくれる。人が人でなくなり、この世界がこの世界でなくなる気にさせてくれる。

バウムクーヘンは、日常から非日常へと誘う入り口なのかもしれない。

ところで、バウムクーヘンの穴だけを残して、バウムクーヘンを食べることはできるのだろうか。