RとPythonと表計算 #02 ポアソン分布

2022年4月8日 07:05

本シリーズ記事は、R言語、Python、表計算ソフトを使った統計解析の手法を、主要な確率分布をテーマに沿ってまとめていきます。
高等学校の数学や情報の授業におけるデータ分析・活用を想定しながら書いてまいります。
特に、私のように「Pythonと比較しながらRも学習してみよう」と思っている方にお読みいただけますと嬉しく思います。

第2回はポアソン分布について整理していきたいと思っています。

Pythonは下記のライブラリの読込はすでに行っているものとします。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats

概要

二項分布$${ B(n, p) }$$で試行回数$${ n }$$が極めて大きく、成功確率$${ p }$$が極めて小さいような場合の確率分布をポアソン分布（Poisson distribution）といいます。
これは、ある時間間隔で発生する事象の回数を表す確率分布とも言えます。もう少し詳しく述べていきましょう。

確率変数$${ X }$$が二項分布$${ B(n, p) }$$に従うものとします。
$${ n }$$が極めて大きく、成功確率$${ p }$$が極めて小さいとき、$${ np = \lambda }$$とおきます。この$${ \lambda }$$は一定の試行回数や時間間隔で事象の発生する回数の平均であることに注意してください。
このとき、$${ X }$$は平均$${ \lambda }$$のポアソン分布$${ Po(\lambda) }$$に従うといいます。

例えば、ある工場ではある製品を製造するときに不良品が0.03%の確率で出てしまうとします。つまり、発生確率は$${ p = 0.0003}$$で極めて小さいといえます。
これを10000個製造するとき、つまり試行回数$${ n = 10000 }$$のときの不良品の個数$${ X }$$が従う分布がポアソン分布ということです。
このとき、$${ \lambda = 10000 \times 0.0003 = 3}$$が10000個製造したときの不良品の個数の平均であり、$${ X }$$は平均$${ 3 }$$のポアソン分布$${ Po(3) }$$に従うというわけです。

確率質量関数

確率変数$${ X }$$が平均$${ \lambda }$$のポアソン分布$${ Po(\lambda) }$$に従うときの確率は次の式で与えられます。

$$
P(X=r) = e^{-\lambda} \frac{\lambda^r}{r!} \quad (r=0,1,2, \cdots )
$$

（$${ \lamabda }$$ : 平均=試行回数×発生確率，$${ r }$$: 発生回数）

まず、次の確率をR・Python・表計算ソフトで求めます。

[例]　ある工場ではある製品を製造するときに不良品が0.03%の割合で含まれる。この工場の製品10000個取り出したときに、不良品がちょうど5個含まれる確率を求めなさい。

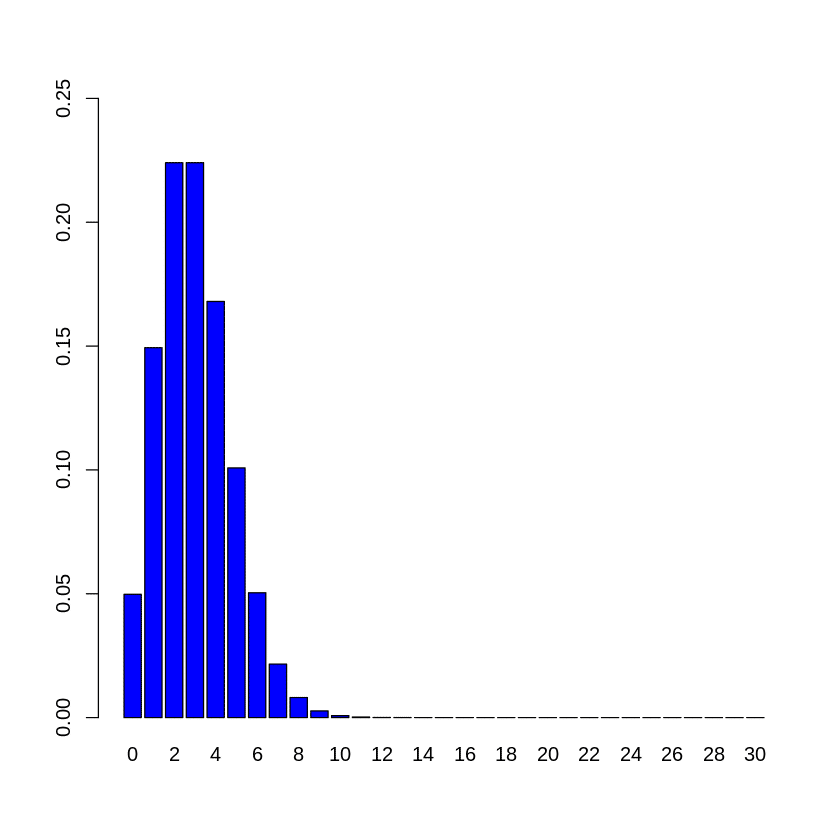
次に、$${ r=0,1,2 \cdots , 30 }$$として、$${ r }$$を横軸に、「不良品がちょうど$${ r }$$個含まれる確率」を縦軸にとった棒グラフを描画することにします。

上でも確認しましたが、10000個製造したときの不良品の個数$${ X }$$が、平均$${ \lambda = 10000 \times 0.0003 = 3}$$のポアソン分布$${ Po(3) }$$に従うことを利用して求めていきます。

R

dpois(発生回数, $${ \lambda }$$)

dpois(5,3)

実行結果：0.100818813444924

x <- 0:30
lam <- 3
barplot(dpois(x,lam), ylim=c(0, 0.25), names.arg = x ,col="blue")

実行結果：

Python

stats.poisson.pmf(発生回数, $${ \lambda }$$)

stats.poisson.pmf(5,3)

実行結果：0.10081881344492458

x = np.arange(0,31,1)
lam = 3
pm = stats.poisson.pmf(x, lam)
plt.bar(x, pm, color = "blue")
plt.grid()
plt.show()

実行結果：

表計算ソフト

=POISSON.DIST(発生回数, $${ \lambda }$$, false)

グラフの種類：縦棒グラフ
データ範囲：A1:B32

累積分布関数

確率変数$${ X }$$が平均$${ \lambda }$$のポアソン分布$${ Po(\lambda) }$$に従うとします。
このとき、$${ X }$$の累積分布関数$${ F(r) }$$は次の式で与えられます。

$$
F(r) = P(X\leqq r) = \sum_{k=0}^r e^{-\lambda} \frac{\lambda^k}{k!}
$$

これは、一定の試行回数や時間間隔で事象の発生する回数が$${ r }$$回以下であるような確率を表しています。

次の確率をR・Python・表計算ソフトで求めます。

[例]　ある工場ではある製品を製造するときに不良品が0.03%の割合で含まれる。この工場の製品10000個取り出したときに、含まれる不良品の数が5個以下である確率を求めなさい。

また、$${ r=0,1,2 \cdots , 30 }$$として、$${ r }$$を横軸に、「不良品が$${ r }$$個以下含まれる確率」を縦軸にとった棒グラフを描画することにします。

R

ppois(発生回数, $${ \lambda }$$)

ppois(5,3)

実行結果：0.916082057968697

x <- 0:30
n <- 30
p <- 1/6
barplot(pbinom(x,n,p),names.arg = x, col="green")

実行結果：

Python

stats.poisson.cdf(発生回数, $${ \lambda }$$)

stats.poisson.cdf(5,3)

実行結果：0.9160820579686966

x = np.arange(0,31,1)
lam = 3
cd = stats.poisson.cdf(x, lam)
plt.bar(x, cd, color = "green")
plt.grid()
plt.show()

実行結果：

表計算ソフト

=BINOM.DIST(成功回数, 試行回数, 成功確率, true)

グラフの種類：縦棒グラフ
データ範囲：A1:A32, C1: C32

分位点

累積分布関数の逆関数であるパーセントポイント関数の値のことです。
つまり、確率変数$${ X }$$がポアソン分布$${ Po(\lambda) }$$に従うとき、$${ X }$$の$${ 100\alpha }$$%点とは、$${ P(X \leqq r ) \geqq \alpha }$$となる最小の自然数$${ r }$$のことを言います。

次の例を考えます。これは有意水準5%で片側検定を行うときの棄却域を求める問題です。

[例]　ある工場ではある製品を製造するときに不良品が0.03%の割合で含まれる。この工場の製品10000個取り出したときに$${ r }$$個以上の不良品がある確率は5%未満となる。このような自然数$${ r }$$の最小値を求めなさい。（上側5%点）

これは、$${ P(X \leqq r ) \geqq 0.95 }$$となる最小の自然数$${ r }$$を求める問題に他なりません。

R

qpois(累積確率, $${ \lambda }$$)

qpois(0.95,3)

実行結果：6

これは${ P(X \leqq r ) \geqq 0.95 }$$となる最小の自然数$${ r }$$の値が6であることを意味しています。

Python

stats.poisson.ppf(累積確率, $${ \lambda }$$)

stats.poisson.ppf(0.95,3)

実行結果：6.0

これは${ P(X \leqq r ) \geqq 0.95 }$$となる最小の自然数$${ r }$$の値が6であることを意味しています。

表計算ソフト

ポアソン分布のパーセントポイント関数（POISSON.INV関数）は表計算ソフトに用意されていません。

従いまして、下のような表を作成して累積確率を上から見ていき、0.95を超えるような発生回数を探す方法が分かりやすいです。

または次のように二項分布で近似します。

確率変数$${ X }$$がポアソン分布$${ Po(3) }$$に従うとき、

$${ \lambda = 3 = 10000 \times 0.0003 }$$

より、$${ X }$$は二項分布$${ B(10000,0.0003) }$$に従うと考えて、

=BINOM.INV(10000, 0.0003, 0.95)

を入力することで、代用をするという発想です。

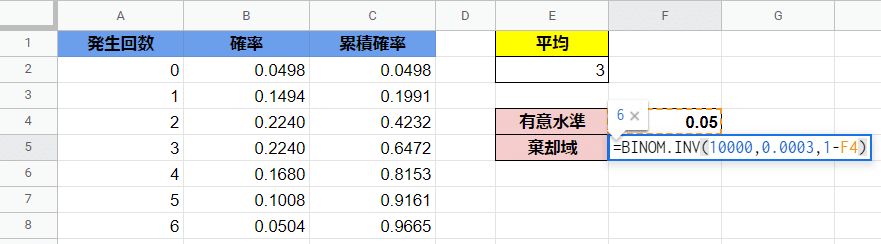
セルF5には6が出力されます。
実際に、上図の列Cを見れば、5回以下の確率が約0.9161、6回以下の確率が0.9665であることが分かります。

期待値と分散

確率変数$${ X }$$が二項分布$${ Po(\lambda) }$$に従うとき、$${ X }$$の期待値$${ E(X) }$$と分散$${ V(X) }$$は次の式で与えられます。

$$
E(X) = \lambda ,\quad V(X) = \lambda
$$

Python

Pythonでは、ポアソン分布に従う確率変数を定義して、その確率変数の期待値や分散を次のように求めることができます。

X = stats.poisson(3)    # Xはポアソン分布Po(3)に従う
print(f"E(X) = {X.mean()}, V(X) = {X.var()} ")

実行結果：E(X) = 3.0, V(X) = 3.0

次回は「負の二項分布」についてまとめます。
最後までお読みいただきありがとうございました。