【第27回】数撃てば当たるのか? - 幾何分布編
下手な鉄砲も数撃ちゃ当たる。
今回は、ある日の高等学校情報の授業のエピソードからです。
シミュレーション
サイコロを100回投げて1の目が35回以上出ることがいかに珍しいのかという話をしていました(「シミュレーション」を学ぶ回)。
これを実際に体験してもらおうと、Pythonで次のようなプログラムを生徒に作ってもらい実行するような実習です。
import numpy as np
dice = np.random.randint(1,7,100)
print(dice)
dice01 = np.count_nonzero(dice == 1)
print(f"1の目の出た回数は{dice01}回です。") これは、1から6の整数の乱数を100個発生させ、100個のうち、1が何個あるかを数えるような命令です。
試しに1回、実行してみますと、次のような結果が出てきました。

公正なサイコロを1回投げて1の目が出る確率は$${ \frac{1}{6} }$$ですから、だいたい16~17回あたりが多く出ます。35回以上はなかなか出ません。
実際、公正なサイコロを繰り返し100回投げて1の目が35回以上出る確率は、0.0007%(100万分の7)ですので、それもそのはずです。
これをPythonを使って求めると、次のコードになります。
from scipy import stats
stats.binom_test(35,100,1/6,alternative="greater")実行結果は、7.025087033741793e-06($${ 7.025087033741793 \times 10^{-6} }$$)です。
生徒の興味から
ここから、仮説検定の考え方の話に進めていこうと思ったのですが、この低い確率を見てスイッチが入ったのか、「35回以上を最初に出せた人が勝ち」みたいな変な競争が生徒の間で自然発生的に起こりました。
いやいや、頑張るところ、違うってw
でも、こういうところが生徒は興味を持つのかと思い、少しの間、授業を進めずに様子を見てました。
2分後にこの競争の勝者(?)が現れました。
スマートに下記のコードを実行した生徒でした。
dice01 = 0
i = 0
while dice01 < 35:
i = i + 1
dice = np.random.randint(1,7,100)
dice01 = np.count_nonzero(dice == 1)
print(f"{i}回目に1の目が35回以上出ました。出た回数は{dice01}回です。")
print(dice)実行結果:

whileループか!
なるほど。これまでの学習をよく活かしたと思わず感心してしまいました。
ちなみに他の生徒から「ズルい」という声が上がっていましたが、これは作戦勝ちだと思います。
ちょっと脱線
勝者の出現により、生徒は乱数を発生させることに興味はなくなりました。
一方で…
「これは面白い話題だ。」
と今度は私の方がスイッチが入ってしまいました。
定式化
今回のことを次のような問いにしてみます。
1回の試行で起こる確率がおよそ0.0007%であるような事象がある。
この試行を繰り返し行ったときに200000回目までに少なくとも1回、この事象が起こる確率を求めよ。
これは「20万回目までに1回も出ない」の余事象であることに注意し、次のようなコードを実行して求めることにしました。
p = stats.binom_test(35,100,1/6,alternative="greater")
1- (1-p) ** 200000実行結果は、0.7546384254669136(およそ75%)です。
つまり20万回目行えば、少なくとも1回は起こる確率はそれなりに高いということです。正に「下手な鉄砲も数撃ちゃ当たる」です。
そうなってくると、次に気になるのは、1回の試行で起こる確率がおよそ0.0007%であるような事象はおおよそ何回目の試行で起こることが期待できるかという問題です。
幾何分布
成功確率(この場合は、1の目が100回中35回以上出る確率)が$${ p }$$であるような、独立した試行を繰り返すとき、初めて成功する回数$${ X }$$の従う確率分布を幾何分布といいます。
$${ k }$$回目で初めて成功する確率$${ P(X=k) }$$は次の式で表されます。
$$
P(X=k) = (1-p)^{k-1} p \qquad ( k=1,2,3, \cdots )
$$
今回の場合は、$${ p = 7.025087033741793 \times 10^{-6} }$$です。
$${ k }$$を横軸に、$${ P(X=k) }$$を縦軸にとって、グラフを描いてみたいと思います。
import numpy as np
import matplotlib.pyplot as plt
k = np.arange(1,600000,1)
p = stats.binom_test(35,100,1/6,alternative="greater")
plt.plot(k, (1-p)**(k-1) * p)
plt.grid()
plt.show()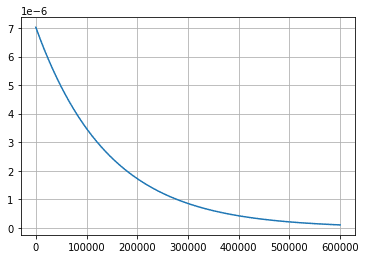
初めて成功する回数が大きくなるほど確率が減少していきます。
なお、plt.plot(k, (1-p)**(k-1) * p)を用いる代わりに、次のようにコードを記述することもできます。
X = stats.geom(p) # Xは成功確率pの幾何分布に従う
plt.plot(k, X.pmf(k)) # pmf(確率質量関数)一方で私たちが知りたいのは、「初めて成功する回数が$${ k }$$回目である確率」よりも、「$${ k }$$回目までに成功する確率」です。
例えば、5万回繰り返した時に成功する確率はどれくらいなのかが興味があるわけです。これもグラフで表してみましょう。
次のようなコードを書きます。
k = np.arange(1,600000,1)
p = stats.binom_test(35,100,1/6,alternative="greater")
X = stats.geom(p) # Xは成功確率pの幾何分布に従う
plt.plot(k, X.cdf(k)) # cdf(累積分布関数)
plt.grid()
plt.show()上のコードのpmfのところをcdfに変えるだけですね。
実行すると次のようなグラフが出力されます。

これを見ると、10万回くらい繰り返すと50%くらいの確率で成功し、60万回繰り返すと100%に近い確率で成功することが分かります。
幾何分布の期待値
成功確率が$${ p }$$の幾何分布に従う確率変数$${ X }$$の期待値は、$${ \frac{1}{p} }$$であることが知られています。
簡単に言うと、平均して$${ \frac{1}{p} }$$回目で初めてそれが起こるということです。
これは証明しようと思うと無限級数のよい練習問題なのですが、直観的に理解してみたいと思います。
例えば、サイコロを1回投げて1の目が出る確率は$${ p=\frac{1}{6} }$$です。
したがって、平均すると$${ \frac{1}{p} = 6 }$$回目には1の目が出てくることが期待できそうですね。
では今回の場合を計算してみましょう。
p = stats.binom_test(35,100,1/6,alternative="greater")
print(1/p)これを実行すると、142346.99089092523が出力されます。
すなわち、およそ142347回目の試行で「1の目が100回中35回以上出る」ということが期待されることが分かりました。
まとめ
今回は、授業中の生徒とのやり取りから、ふと興味を持ったことについて、記事を書いてみました。
生徒の興味と試行錯誤から話が膨らみ、授業としては完全に脱線してしまいましたが、思いがけない形で深い内容になり、私にとっても良い学びだったと振り返ります。
生徒の興味が私の興味を刺激し、私の興味がまた生徒を刺激できるような相互作用を、来年度は授業の中でもっと生み出していきたいと思いました。
最後までお読みいただきありがとうございました。
