【第15回】母比率の検定
前回の記事では、下記の例題を通して仮説検定の考え方を学びました。
例題
あるサイコロを100回投げたところ、1の目が35回出た。このサイコロは1の目が出やすいような歪みがあると判断してもよいか。有意水準1%で検定しなさい。
詳しい内容は、前回の記事をご覧ください。
こちらの問題はシンプルで、最初に考え方を学ぶという意味では分かりやすいのですが、すでにモデル化されている問題であるために社会の問題に関わっていることは実感しにくいという欠点があります。
そこで今回は、標本から母集団の特徴を推測していることを捉えやすい問題を扱うことを通して、前回学んだ内容を深めて参りたいと思います。本質的な部分は前回と同じで、母比率(母集団における比率)を検定する問題を考えます。
今回考える問題
「高等学校学習指導要領(平成30年公示)解説 数学編 理数編」では、次のような具体例が示されています。
例えば「ある新素材の枕を使用した30人のうち80%にあたる24人が以前よりよく眠れたと回答した」という結果に対して、新素材の枕を使用するとよく眠ることができると判断できるか、という問題に取り組ませることを考える。
こちらをもとに次のような問題を考えてみたいと思います。
例題
枕を製造している会社がすでに販売している枕を改良して、ある新素材の枕を開発した。無作為に選んだ30人の消費者にこれらの枕を使って比較してもらったところ、24人が以前よりよく眠れたと回答した。この回答のデータから消費者全体の半数超が「新素材の枕を使用するとよく眠ることができる」と回答すると判断できるか。有意水準5%で検定しなさい。
この問題では消費者全体を母集団と考え、その中から無作為に抽出した30人からなる標本を調査しています。標本において「新素材の枕を使用するとよく眠れた」と回答した割合(標本比率)が80%であることをもって、母集団におけるその割合(母比率)が50%を超えていると判断できるどうかを考える問題です。

母比率の検定
それでは、前回の流れに沿って考えていきましょう。まずはこれから主張したいこと(対立仮説)とそれに反する主張(帰無仮説)を確認してみましょう。
帰無仮説と対立仮説
まずは、問題の設定に合わせて大雑把に捉えますと下記の通りです。
帰無仮説:新素材の枕を使った寝心地は従来品と変わらない。
対立仮説:新素材の枕は、従来品から改良されている。
これを母比率を使ってもう少し正確に表現すると次のようになります。
母集団において「新素材の枕を使用するとよく眠れた」と回答する割合、すなわち、母比率を$${ p }$$とすると、
帰無仮説: $${ p=1/2 }$$ 対立仮説: $${ p>1/2 }$$
として、有意水準5%で検定します。
p値を求める
帰無仮説が正しいという仮定、つまり従来の枕と新素材の枕がともに確率$${ 1/2 }$$で選ばれるという仮定のもとで、30名のうち24名以上が「新素材の枕を使用するとよく眠れた」と回答する確率がp値になります。
この状況はコイントスと全く同じです。すなわち、公正なコインを30回投げて24回以上表が出る確率を求めると考えればより分かりやすいですね。
前回と同じように、Pythonを利用してその確率を求めてみます。
from scipy import stats
stats.binom_test(24, 30, 0.5, alternative="greater")これを実行しますと、0.0007154531776905064が出力されます。
結論
今回の有意水準は5%(0.05)です。これは帰無仮説の仮定のもとで現在観測されていることやそれよりも極端なことが起こる確率が5%を下回った場合に、帰無仮説を棄却しましょうという取り決めでした。
今回のp値は0.0007154531776905064で、有意水準0.05よりも小さいため、帰無仮説は棄却されます。
したがって、新素材の枕は、従来品から改良されていると判断してもよいということになりました。
補足
仮説検定としては以上ですが、ここで少し補足をしてみたいと思います。30回コインを投げたときの表の出る回数$${X}$$の確率分布をグラフで見てみたいと思います。Pythonを使って描画します。
import numpy as np
import matplotlib.pyplot as plt
k = np.arange(0, 31, 1)
plt.bar(k, stats.binom.pmf(k, 30, 0.5))
plt.grid()
plt.show()
気をつけたいのは、抽出した標本の8割以上が「新素材の枕を使用するとよく眠れた」と回答すれば、新素材の枕は、従来品から改良されていると判断できるという結論ではありません。標本の大きさが非常に大事です。
直感的にも、「10名のうち8名」よりも「100名のうち80名」が改良したと回答したという情報をもとにしたほうが、母集団に対する推測に確信を持てると思われます。
それでは、実際にこれらの場合のp値を求めてみたいと思います。
10名のうち8名
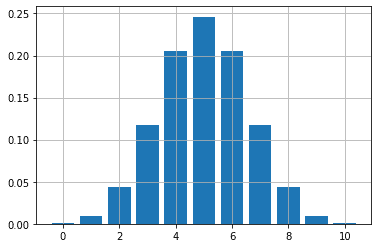
コインを10回投げて表が8回以上出る確率を求めます。
stats.binom_test(8, 10, 0.5, alternative="greater")実行しますと、0.054687500000000014が出力されます。このp値が有意水準の0.05を超えていますので、今回は帰無仮説を棄却できません。
従いまして「新素材の枕は従来品から改良されたと言い切れない」というのがこの結論になります。
帰無仮説を棄却できないというのは、帰無仮説が正しいことの判断ではなく、あくまでこれが「誤っていると判断できない」という意味です。これをもって「新素材の枕は従来品から改良されていない」という判断をしているわけではないことに注意をしたいところです。
上と同様にグラフをかきますと次のようになります。
100名のうち80名
最初の30名の標本での議論から、こちらは帰無仮説が棄却されることがすでに分かっていますが、どれくらいp値が小さいか見てみましょう。
コインを100回投げて表が80回以上出る確率を求めます。
stats.binom_test(80, 100, 0.5, alternative="greater")実行しますと、5.579544528625975e-10が出力されます。これは、およそ0.000000000558(小数第10位に初めて0以外)です。
このp値は有意水準0.05よりも小さいため、帰無仮説は棄却されます。
上と同様にグラフをかきますと次のようになります。

コインを投げるという試行の回数が多ければ多いほど、確率分布を表した棒グラフは平均値をピークにした山型の滑らかな曲線に近づきます。
ここは、次回の「正規分布」の記事でまとめていきたいと思っています。
最後に
今回は母比率の検定について、前回内容を踏まえて整理をしました。
今回記事をまとめてみて、コンピュータを活用してシミュレーションを行ったり、具体的に確率を求めたり、グラフを描いたりしながら仮説検定の考え方を学んでいく意義は大きいと感じました。これからさらに実践と研究を重ねつつ、数学と情報の授業のより良い連携方法を探っていきたいと考えております。
数学Iの教科書で扱われている「仮説検定の考え方」の内容としては今回の記事の内容で完結をしているのですが、仮説検定については次回以降、もう少し掘り下げて記事を書き進めていきたいと考えています。
最後までお読みいただき、ありがとうございました。
