
RとPythonと表計算 #03 負の二項分布
本シリーズ記事は、R言語、Python、表計算ソフトを使った統計解析の手法を、主要な確率分布をテーマに沿ってまとめていくものです。
高等学校の数学や情報の授業におけるデータ分析・活用を想定しながら書いてまいります。
特に、私のように「Pythonと比較しながらRも学習してみよう」と思っている方にお読みいただけますと嬉しく思います。
第3回は負の二項分布について整理していきたいと思っています。
Pythonは下記のライブラリの読込はすでに行っているものとします。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats概要
成功と失敗のある試行を行い、 その試行が「$${ r }$$回成功するまでに$${ k }$$回失敗する確率」の分布を表すのが負の二項分布です。
もう少し詳しく見てみましょう。
成功確率$${ p }$$のベルヌーイ試行を繰り返すとします。
試行を繰り返すことの終了条件を「$${ r }$$回成功するまで」とし、$${ r }$$の値を固定して、そこまでに失敗する回数を$${ X }$$としたときの確率変数$${ X }$$の従うが負の二項分布です。
このとき、$${ X }$$は成功回数$${ r }$$,成功確率$${ p }$$の負の二項分布$${ NB(r,p) }$$に従うといいます。
確率質量関数
確率変数$${ X }$$が成功回数$${ r }$$,成功確率$${ p }$$の負の二項分布$${ NB(r,p) }$$に従うとき、$${ X=k }$$となる確率、すなわち「$${ r }$$回成功するまでに$${ k }$$回失敗する確率」は次の式で与えられます。
$$
P(X=k) = _{r+k-1}C_{r-1} (1-p)^k p^r\quad (k=0,1,2, \cdots )
$$
($${ p }$$ : 成功確率,$${ r }$$: 成功回数)
やや分かりにくいですので、下に具体例を示します。

まず、次の確率をR・Python・表計算ソフトで求めます。
[例] サイコロを1の目が3回出るまで繰り返し投げる。
ちょうど10回目で終わる確率を求めなさい。
これは、「3回成功するまでに7回失敗する確率」を求める問題です。
失敗回数$${ X }$$は「成功回数$${ r=3 }$$、成功確率$${ p= \frac{1}{6} }$$の負の二項分布$${ NB(3,\frac{1}{6} ) }$$」に従います。
このときの確率質量関数は、次の式で与えられます。
$$
P(X=k) = _{3+k-1}C_{3-1}( \frac{5}{6})^k (\frac{1}{6})^3 = _{k+2}C_2 (\frac{5}{6})^k (\frac{1}{6})^3
$$
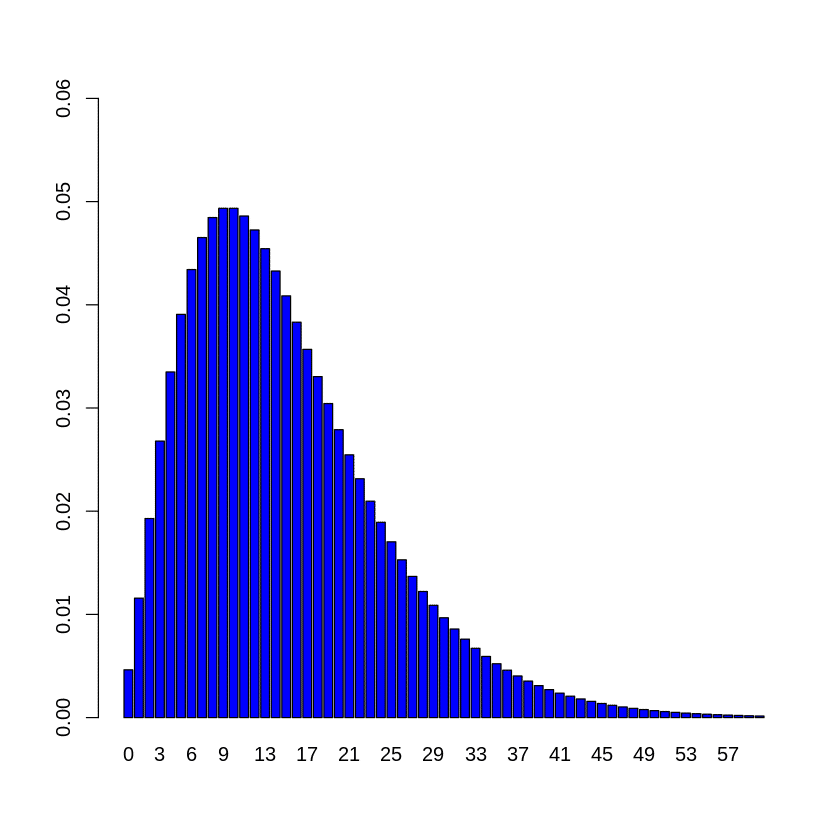
また、$${ k=0,1,2 \cdots , 60 }$$として、$${ k }$$を横軸に、「1の目が3回出るまでに1以外の目がちょうど$${ k }$$回出る確率」を縦軸にとった棒グラフも描画することにします。
R
dnbinom(失敗回数, 成功回数, 成功確率)
dnbinom(7,3,1/6)実行結果:0.0465136078722755
k <- 0:60
r <- 3
p <- 1/6
barplot(dnbinom(k,r,p), ylim=c(0, 0.06), names.arg = k ,col="blue")実行結果:
Python
stats.nbinom.pmf(失敗回数, 成功回数, 成功確率)
stats.nbinom.pmf(7,3,1/6)実行結果:0.0465136078722755
k = np.arange(0,61,1)
r = 3
p = 1/6
pm = stats.nbinom.pmf(k,r,p)
plt.bar(k, pm, color = "blue")
plt.grid()
plt.show()実行結果:

表計算ソフト
=NEGBINOM.DIST(失敗回数, 成功回数, 成功確率)
本記事投稿時においては、Excelでは4つ目の引数でブール値(falseやtrue)を指定することで確率質量関数の値か累積分布関数の値かを選択できるのですが、Googleスプレッドシート関数ではこちらの指定ができません。
常にfalseの場合(確率質量関数の値)になることに注意してください。

グラフの種類:縦棒グラフ
データ範囲:A1:B62

累積分布関数
確率変数$${ X }$$は成功回数$${ r }$$,成功確率$${ p }$$の負の二項分布$${ NB(r,p) }$$に従うとします。
このとき、$${ X }$$の累積分布関数$${ F(x) }$$は次の式で与えられます。
$$
F(x) = P(X\leqq x) = \sum_{k=0}^x _{r+k-1}C_{r-1} (1-p)^k p^r
$$
これは、$${ r }$$回成功するまでの失敗回数が$${ x }$$回以下である確率を表しています。
次の確率をR・Python・表計算ソフトで求めます。
[例] サイコロを1の目が3回出るまで繰り返し投げるとき、10回以下で終わる確率を求めなさい。
これは「3回成功するまでの失敗回数が7回以下である確率」を求める問題です。
これを求めた後に、$${ k=0,1,2 \cdots , 60 }$$として、$${ k }$$を横軸に、「1の目が3回出るまでに1以外の目が$${ k }$$回以下出る確率」を縦軸にとった棒グラフを描画することにします。
R
pnbinom(失敗回数, 成功回数, 成功確率)
pnbinom(7,3,1/6)実行結果:0.224773202128741
k <- 0:60
r <- 3
p <- 1/6
barplot(pnbinom(k,r,p), ylim=c(0, 1),names.arg = k, col="green")実行結果:

Python
stats.nbinom.cdf(失敗回数, 成功回数, 成功確率)
stats.nbinom.cdf(7,3,1/6)実行結果:0.22477320212874052
k = np.arange(0,61,1)
r = 3
p = 1/6
cd = stats.nbinom.cdf(k,r,p)
plt.bar(k, cd, color = "green")
plt.grid()
plt.show()実行結果:

表計算ソフト
前述の通り、本記事投稿時においては、GoogleスプレッドシートではNEGBINOM.DIST関数を利用して累積分布関数の値を求めることができません。(Excelでは可能です。)
従いまして、ここでは確率質量関数の和をとることで代替します。
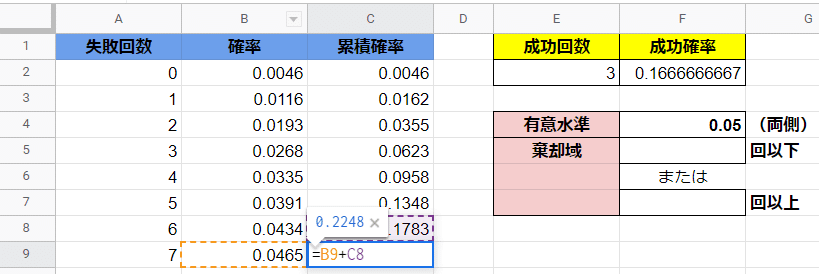
グラフの種類:縦棒グラフ
データ範囲:A1:A62, C1: C62

分位点
累積分布関数の逆関数であるパーセントポイント関数の値のことです。
つまり、確率変数$${ X }$$は成功回数$${ r }$$,成功確率$${ p }$$の負の二項分布$${ NB(r,p) }$$に従うとき、$${ X }$$の$${ 100\alpha }$$%点とは、$${ P(X \leqq r ) \geqq \alpha }$$となる最小の自然数$${ r }$$のことを言います。
次の例を考えます。
これは有意水準5%で両側検定を行うときの棄却域を求める問題です。
これまでの2回の記事では片側検定を見てきましたが、今回は両側検定で考えますので、ご注意ください。
[例] サイコロを1の目が3回出るまで繰り返し投げる。
失敗回数が何回以下になる確率、何回以上になる確率がそれぞれ2.5%以下になるかを求めなさい。(両側5%点)
これは、$${ P(X \leqq x_1) \leqq 0.025 かつ P(X \leqq x_2) \geqq 0.975 }$$となる最小の自然数$${ x_1 , x_2 }$$をそれぞれ求める問題に他なりません。
R
qnbinom(累積確率, 成功回数, 成功確率)
qnbinom(0.025,3,1/6)実行結果:2
これは$${ P(X \leqq r ) \geqq 0.025 }$$となる最小の自然数$${ r }$$の値が2であることを意味しています。
したがって、$${ P(X \leqq r ) \leqq 0.025 }$$となる最小の自然数は1であることに注意です。
qnbinom(0.975,3,1/6)実行結果:38
これは$${ P(X \leqq r ) \geqq 0.975 }$$となる最小の自然数$${ r }$$の値が38であることを意味しています。
以上より、有意水準5%の両側検定における棄却域は、失敗回数が「1回以下または38回以上」となります。
Python
stats.nbinom.ppf(累積確率, 成功回数, 成功確率)
詳しい説明は上のRの場合と同じです。
ここでは、下側2.5%点と上側2.5%点を同時に求めます。
print(stats.nbinom.ppf(0.025,3,1/6), stats.nbinom.ppf(0.975,3,1/6))実行結果:2.0 38.0
この実行結果より、上のRでの説明と同じ結論を得ます。
表計算ソフト
Excel・Googleスプレッドシートとも、負の二項分布に対してもパーセントポイント関数は用意されていません。
累積確率を入力した列を見て、下側2.5%点と上側2.5%点を見つけます。

下側2.5%点:失敗回数1回と2回の間 → 1回
$${ 失敗回数1回: 0.0162<0.025、失敗回数2回: 0.0355 > 0.025 }$$
上側2.5%点:失敗回数37回と38回の間 → 38回
$${ 失敗回数37回: 0.9726<0.975、失敗回数38回: 0.9762 > 0.975 }$$
期待値と分散
確率変数$${ X }$$が成功回数$${ r }$$,成功確率$${ p }$$の負の二項分布$${ NB(r,p) }$$に従うとき、$${ X }$$の期待値$${ E(X) }$$と分散$${ V(X) }$$は次の式で与えられます。
$$
E(X) = \frac{r(1-p)}{p} ,\quad V(X) = \frac{r(1-p)}{p^2}
$$
Python
Pythonでは、負の二項分布に従う確率変数を定義して、その確率変数の期待値や分散を次のように求めることができます。
X = stats.nbinom(3,1/6) # Xは負の二項分布NV(3,1/6)に従う
print(f"E(X) = {X.mean()}, V(X) = {X.var()} ")実行結果:E(X) = 15.0, V(X) = 90.0
次回は、負の二項分布の特別な場合である「幾何分布」についてまとめます。
最後までお読みいただきありがとうございました
