
第6章 機械学習プロセス編: 第二節 情報理論と利用して特徴量を分析する
こんにちは、今回の内容は短めですので、ランチ休憩で書いちゃいます(笑)
情報理論とは
説明変数と結果の間の相互情報量(MI)は、2つの変数間の相互依存関係の尺度です。相関関係の概念を非線形関係に拡張します。より具体的には、ある確率変数について得られた情報を、他の確率変数を介して定量化します。
MIの概念は、確率変数のエントロピーの基本的な概念と密接に関連しています。エントロピーは、確率変数に含まれる情報の量を定量化します。
正式には、2つの確率変数XおよびYの相互情報(I(X、Y))は、次のように定義されます。

ここで、p(X,Y)はX,Yの同時確率質量関数、p_X とp_YはそれぞれXとYの周辺確率質量関数である。
sklearn関数はfeature_selection.mutual_info_regressionを実装しており、すべての特徴量と継続的な結果の間の相互情報を計算して、予測情報を含む可能性が最も高い機能を選択します。分類バージョンもあります(詳細については、ドキュメントを参照してください)。
このノートブックには、第4章「アルファファクターリサーチ」で作成した財務データへのアプリケーションが含まれています。
インポートと設定
import warnings
warnings.filterwarnings('ignore')%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.feature_selection import mutual_info_classifsns.set_style('whitegrid')
idx = pd.IndexSliceデータを取得
with pd.HDFStore('../data/assets.h5') as store:
data = store['engineered_features']本データはアメリカの上場企業約3000社の2001年1月31日~2018年2月28日までのデータである。特徴量として、リターンや終値等があるが、具体的な特徴量の生成方法等については以前書いた特徴量エンジニアリングの記事をご参照ください。
ダミー変数を作成
dummy_data = pd.get_dummies(data,
columns=['year','month', 'msize', 'age', 'sector'],
prefix=['year','month', 'msize', 'age', ''],
prefix_sep=['_', '_', '_', '_', ''])
dummy_data = dummy_data.rename(columns={c:c.replace('.0', '') for c in dummy_data.columns})
dummy_data.info()
'''
<class 'pandas.core.frame.DataFrame'>
MultiIndex: 397126 entries, ('A', Timestamp('2001-01-31 00:00:00')) to ('ZUMZ', Timestamp('2018-02-28 00:00:00'))
Data columns (total 88 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 return_1m 397126 non-null float64
1 return_2m 397126 non-null float64
2 return_3m 397126 non-null float64
3 return_6m 397126 non-null float64
4 return_9m 397126 non-null float64
5 return_12m 397126 non-null float64
6 Mkt-RF 397126 non-null float64
7 SMB 397126 non-null float64
8 HML 397126 non-null float64
9 RMW 397126 non-null float64
10 CMA 397126 non-null float64
11 momentum_2 397126 non-null float64
12 momentum_3 397126 non-null float64
13 momentum_6 397126 non-null float64
14 momentum_9 397126 non-null float64
15 momentum_12 397126 non-null float64
16 momentum_3_12 397126 non-null float64
17 return_1m_t-1 394727 non-null float64
18 return_1m_t-2 392328 non-null float64
19 return_1m_t-3 389929 non-null float64
20 return_1m_t-4 387530 non-null float64
21 return_1m_t-5 385132 non-null float64
22 return_1m_t-6 382737 non-null float64
23 target_1m 397126 non-null float64
24 target_2m 394727 non-null float64
25 target_3m 392328 non-null float64
26 target_6m 385132 non-null float64
27 target_12m 370770 non-null float64
28 year_2001 397126 non-null uint8
29 year_2002 397126 non-null uint8
30 year_2003 397126 non-null uint8
31 year_2004 397126 non-null uint8
32 year_2005 397126 non-null uint8
33 year_2006 397126 non-null uint8
34 year_2007 397126 non-null uint8
35 year_2008 397126 non-null uint8
36 year_2009 397126 non-null uint8
37 year_2010 397126 non-null uint8
38 year_2011 397126 non-null uint8
39 year_2012 397126 non-null uint8
40 year_2013 397126 non-null uint8
41 year_2014 397126 non-null uint8
42 year_2015 397126 non-null uint8
43 year_2016 397126 non-null uint8
44 year_2017 397126 non-null uint8
45 year_2018 397126 non-null uint8
46 month_1 397126 non-null uint8
47 month_2 397126 non-null uint8
48 month_3 397126 non-null uint8
49 month_4 397126 non-null uint8
50 month_5 397126 non-null uint8
51 month_6 397126 non-null uint8
52 month_7 397126 non-null uint8
53 month_8 397126 non-null uint8
54 month_9 397126 non-null uint8
55 month_10 397126 non-null uint8
56 month_11 397126 non-null uint8
57 month_12 397126 non-null uint8
58 msize_-1 397126 non-null uint8
59 msize_1 397126 non-null uint8
60 msize_2 397126 non-null uint8
61 msize_3 397126 non-null uint8
62 msize_4 397126 non-null uint8
63 msize_5 397126 non-null uint8
64 msize_6 397126 non-null uint8
65 msize_7 397126 non-null uint8
66 msize_8 397126 non-null uint8
67 msize_9 397126 non-null uint8
68 msize_10 397126 non-null uint8
69 age_0 397126 non-null uint8
70 age_1 397126 non-null uint8
71 age_2 397126 non-null uint8
72 age_3 397126 non-null uint8
73 age_4 397126 non-null uint8
74 age_5 397126 non-null uint8
75 Basic Industries 397126 non-null uint8
76 Capital Goods 397126 non-null uint8
77 Consumer Durables 397126 non-null uint8
78 Consumer Non-Durables 397126 non-null uint8
79 Consumer Services 397126 non-null uint8
80 Energy 397126 non-null uint8
81 Finance 397126 non-null uint8
82 Health Care 397126 non-null uint8
83 Miscellaneous 397126 non-null uint8
84 Public Utilities 397126 non-null uint8
85 Technology 397126 non-null uint8
86 Transportation 397126 non-null uint8
87 Unknown 397126 non-null uint8
dtypes: float64(28), uint8(60)
memory usage: 109.1+ MB
'''相互情報
特徴量定義
target_labels = [f'target_{i}m' for i in [1,2,3,6,12]]
targets = data.dropna().loc[:, target_labels]
features = data.dropna().drop(target_labels, axis=1)
features.sector = pd.factorize(features.sector)[0]
cat_cols = ['year', 'month', 'msize', 'age', 'sector']
discrete_features = [features.columns.get_loc(c) for c in cat_cols]mutual_info = pd.DataFrame()
for label in target_labels:
mi = mutual_info_classif(X=features,
y=(targets[label]> 0).astype(int),
discrete_features=discrete_features,
random_state=42
)
mutual_info[label] = pd.Series(mi, index=features.columns)mutual_info.sum()正規化MIのヒートマップ
fig, ax= plt.subplots(figsize=(15, 4))
sns.heatmap(mutual_info.div(mutual_info.sum()).T, ax=ax, cmap='Blues');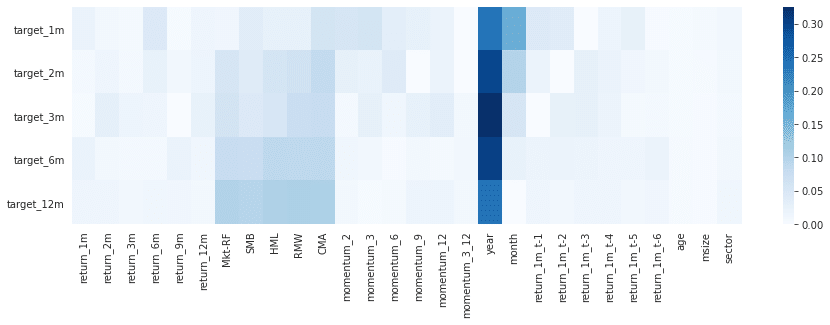
ダミーデータ
target_labels = [f'target_{i}m' for i in [1, 2, 3, 6, 12]]
dummy_targets = dummy_data.dropna().loc[:, target_labels]
dummy_features = dummy_data.dropna().drop(target_labels, axis=1)
cat_cols = [c for c in dummy_features.columns if c not in features.columns]
discrete_features = [dummy_features.columns.get_loc(c) for c in cat_cols]mutual_info_dummies = pd.DataFrame()
for label in target_labels:
mi = mutual_info_classif(X=dummy_features,
y=(dummy_targets[label]> 0).astype(int),
discrete_features=discrete_features,
random_state=42
)
mutual_info_dummies[label] = pd.Series(mi, index=dummy_features.columns)mutual_info_dummies.sum()fig, ax= plt.subplots(figsize=(4, 20))
sns.heatmap(mutual_info_dummies.div(mutual_info_dummies.sum()), ax=ax, cmap='Blues');
まとめ
主にnか月リターンにどういった特徴量が効いているのかについて相互情報量(MI)を利用して調査した。時期によるダミー変数が効いているように見えますが、ボラティリティが大きかった2008年では当然ですので、これを理由に時期によるアノマリーがあると判断するのはお気をつけてください。ここら辺をもっと詳しく調査するためには日次リターンや、特徴量をもっと細かくすることをおすすめします。その他ご自身で作成した特有の特徴量もあるかと思いますので、是非お試しくださいませ(*'ω'*)
この記事が気に入ったらサポートをしてみませんか?
