エントロピーから一気にクライマックス

　皆さんは、何かを続けていて、クライマックスを感じたことはありますか？私はこれまで何回か、それを感じたことがあります。

　たとえ話として、一番いいのは「登山」でしょうか。登っていて疲れてくると、先の長さばかりが気になって、全然進んでいないように思うこともあるのですが、ある高さまで登ると急に周りの景色が開けて、

「ここまで登って来たんだ！」

と実感し、一気に頂上まで向かう気力が湧いてくるのです。それ以降はもうあっという間です。

　クライマックスは、ある時スイッチが入ったみたいに急に来るんです。徐々にではないんです。

　そう考えると、アナログに見える物事も、実はデジタル回路のように「スレッショルド」みたいなものがあるのかもしれませんね。（何の話だ）

　さて、これまで熱力学の話をしてきて、とりあえずはエントロピーの一つの概念までたどり着いたわけです。前回の記事は

　今までは、主に史実を追って、

人間にとって、熱とはどんな概念であったか

ということを見てきたわけですが、これまでの熱力学は、

ある熱的現象の観測から引き出した原理を見出す

のが主であったわけです。

　ところが、1865年にクラウジウスがエントロピーの概念を導入してから、熱力学は「解析的（数学的）手法」によって、一気に抽象化されて行くことになります。今後はそれを見て行くので、数式がたくさん出てきます。

　これまでに、自動車のエンジンや汽力発電の蒸気サイクルを始めとする熱機関が、これだけ高度に進化してしてきたのも、この解析的手法がもたらした成果とも言えます。なので、現在の熱力学の概念を理解しようと思ったら、これは避けて通れないのです。

　熱力学の解析的手法は、クラペイロンが「P-V線図」を用いたことに始まります。「P-V線図」とは、例えば、シリンダのピストンが伸び縮みして元に戻った時、シリンダ内の気体の「圧力"P"」と「体積"V"」がどう変化したかを表すものです（下図右）。

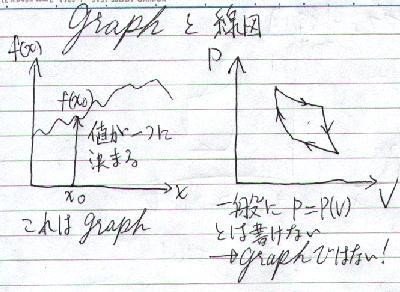
　ちなみに熱力学では、「グラフ」とは呼ばずに「線図」と言います。

　「グラフ」とは数学的に、横軸に"x"を取ったとき、縦軸は例えば"f ( x )"と書いて、

"x"を決めたとき、"f ( x )"の値が一意に決まる関数の関係を表したもの

であるからです（上図）。

　熱力学では合計9つもの変数が出てきて、それらの「従属関係」は、どんなシステムでどんな過程をたどるかによって変わってきます。だから単純なグラフでは描けず、一般的に線図と言うのです。

　さて、気体が"P"という圧力に逆らって、微小体積"dV"だけ膨張したとすると、その気体が外に向ってした微小仕事"δw"は、

δw = PdV

と書けました。これを、「PV仕事」なんて言ったりします。（「プロモビデオ」を作ることではない。）

　この過程を、

ある状態"A"から"B"まで連続的（準静的）に行った

とすると、これは数学的に積分の形で、以下のように書くことができます。

∫[A→B]δw = ∫[A→B]PdV

　つまり、P-V線図の主な目的は、「仕事の出入り」をわかりやすくする事

だと言えます。

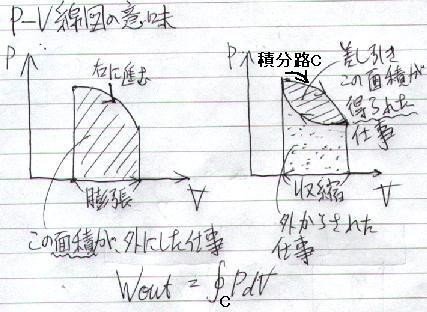
　つまり、あるサイクルにおいて、

P-V線図上の閉曲線の囲む面積

は、

その機関が行った仕事

に対応していることになります。ただし、それはあくまでも「準静的過程」（追記参照）に限ります。

　また、あるサイクルを使って仕事を得ると言うことは、

「P-V線図上で面積を作ること」

と言うこともできます。

　それでは、熱サイクルの主な過程を、P-V線図上に作図してみましょう。体積一定の「定積過程」は、"V"が一定の直線、圧力一定の「定圧過程」は、"P"が一定の直線になるので、これらは問題なく理解可能だと思います。

　問題は、「断熱過程」と「等温過程」です（下図）。

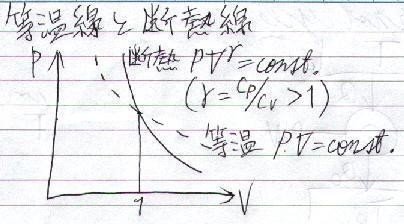
　等温過程は、まず「理想気体の状態方程式」で、温度"T"の変化量をとると、

⊿(PV) = nR⊿T

となります。

　そして、等温条件

⊿T = 0

であるから、

PV = const.（一定）

となるのはいいでしょう。

　「断熱過程」はポアソンの式より、

PV^γ= const.（一定）

γ= Cp/Cv（比熱比）

となります。ちなみに、"Cp"は「定圧熱容量」、"Cv"は「定積熱容量」と言われるもので、一般に「定圧」の時の方が、PV仕事の分熱容量は大きくなります。

　よって、

γ>1

となり、「等温線」より「断熱線」のほうが、「傾き」は急になります。（例えば、"yx = 1"と、"yx^2 = 1"のグラフを書いてみてください。）

　今まで出てきたカルノーサイクルは、この等温線と断熱線の傾きの差を利用して、P-V線図上で面積を作っていた、つまり仕事をしていたのです。そして、この解析的手法を使って、クラウジウスがこれまたうまいことを考えました。

　次回は、それを見ていきたいと思います。今回は、ほんの準備運動でした。

■追記：「準静的」とは

　熱力学ではこの「準静的」にとてもこだわります。それは、微積分を使うには、どちらも「連続的変化である」ということが、数学的に必要条件となっているからです。
　しかし、これは何か問題を解く上では、特に気にする必要はありません。 

　例えば力学でも、重力による「位置エネルギ」は、

U = mgh

と書きます。この定義は、

重力"mg"に逆らって、高さ"h"まで持ち上げるのに要する仕事

です。

　しかし、実際に持ち上げるには、重力"mg"よりもっと大きな力が必要なので、これに要する仕事ももっと大きいはずです。しかし、「準静的」に、ゆーっくり持ち上げたと仮定して、こう書いているわけなのです。
　物理学では解析的手法を使うために、よくこういう仮定をします。しかし、これが実際の現象と良く近似するので、我々はその「計算結果」だけを利用して吟味することができるのです。