【Pythonで統計モデル】SEM1：速習・構造方程式モデリング

2023年6月7日 17:57

はじめに

株式会社GA technologiesの福中です。今、僕は、Advanced Innovation Strategy Center（以下AISC）という部署でChief Data Scientistとして働いています（詳しい自己紹介はAISC WEBサイトのプロフィールをご覧ください）。過去の記事における【Pythonで統計モデル】というシリーズで、因子分析がPythonで問題なく実行できるということを書いてきました。

【Pythonで統計モデル】因子分析編のタイトル
因子分析1：とりあえず1因子モデルを構築してみる
 因子分析2：探索的因子分析の実践
 因子分析3：尺度構成のための因子分析
 因子分析4：カテゴリカル因子分析
 因子分析5：確認的因子分析

今回からは同シリーズの続編、構造方程式モデリング（SEM：Structural Equation Modeling）をPythonで実行する方法について解説していきます。SEMは数理的に非常に柔軟で、統計モデルの中でも群を抜いて複雑で高度な分析手法ですが、Pythonでもかなりのことができることが分かりました。そこで、AISCのデータサイエンスチームで調査したこれらの結果を、リレー形式でブログにまとめていきたいと思います。興味のある方は、ぜひご一読後、AISC Magazineのフォローをお願いします！

注意点

本記事は統計学およびPythonの初心者向け解説記事ではありません。普段からR等を使って統計モデルによる分析や研究を行っている研究者の方が、改めてPythonで構造方程式モデルを行う必要が出た際のリファレンスとしての利用を想定しています。したがって、SEMに不慣れな方は、先に以下で紹介するテキストをはじめとした初心者用の教科書で勉強するとよいと思います。

テキスト

本記事では東京図書から出版されている共分散構造分析［Ｒ編］―構造方程式モデリング―で取り上げられていた事例を、Pythonを使って再現していきます。分析用データは東京図書のホームページからダウンロードできますので、興味のある方はぜひ試してみてください。

環境

本記事の分析は、OS: Windows 11、Python 3.11.2の環境下で行っています。また、必要なパッケージは以下となります。インストール済みの方は割愛してください。

# packageのインストール

pip install numpy pandas matplotlib japanize_matplotlib
pip install graphviz
pip install factor_analyzer
pip install semopy

なおsemopyは構造方程式モデリング（SEM ）を行うためのパッケージで、ドキュメントは以下にあります。

本記事ではここから重要な部分をいくつかピックアップしてご紹介します。網羅的な解説はしませんので、適宜、必要に応じてご参照ください。

SEMとsemopy

構造方程式モデリングとは、観測データや観測変数間の共分散行列をもとに、構成概念や観測変数の関連性を検討するための統計手法です。数理的にも非常に柔軟で、「分析者の仮説をダイレクトに反映したモデリング」が可能であるという特徴を持ちます。

例えば、重回帰分析であれば、「複数の説明変数で1つの従属変数を説明する」という、いわば型のようなものが存在します。しかし、SEMではこのような制約は存在せず、複数の説明変数から複数の従属変数への回帰モデルを構築することができます。またモデリングに利用できる変数は観測変数だけではなく、因子分析で測定した潜在変数に対しても構造を仮定する、いわば潜在変数間の回帰モデルも構築できたりします。このようにSEMがいかに柔軟な統計モデリングであるかがわかるでしょう。

そして、このきわめて柔軟なモデリングを可能にするPythonのパッケージがsemopy (Structural Equation Models Optimization in Python)です。SEMのアプリとしてはMplusやRのlavaanが有名ですが、semopyはlavaanライクに作られているため、これらのSEMのアプリを使ったことがある人なら比較的すぐに慣れることができると思います。特にlavaanとは文法（シンタックス）が極めてよく似ているので、比較的簡単なモデルであればソースコードの中のモデル表現の部分をコピペし、軽微な修正をすることで再利用することができます。semopyの詳しい内容は以下の論文をご参照ください。

semopyの使い方

それではsemopyを利用して、PythonでSEMの分析を行っていきましょう。詳しいシンタックスについてはその都度説明していきます。また、ここではテキストの第2章で利用されているセミナーデータを例にして解説していきます。

パッケージとデータの読み込み

まずはパッケージを読み込みましょう。semopy以外にも、numpyやpandas、matplotlibなど基本的なものが必要になりますので、併せて読み込んでおきましょう。

# packageの読み込み

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
from factor_analyzer.utils import covariance_to_correlation
import semopy

次にデータを読み込みます。データはdatフォルダに格納されているものとします。また、1列目はオブザベーション名にしたいので、index_col=0を指定します。

# データの読み込み

X = pd.read_csv("dat/seminar.csv", encoding='shift_jis', index_col=0)
X.head()

このデータはとあるセミナーにおいて、「充実感」と「講師の質」の関係性を検討するために収集したデータで、すべて5件法で測定されています。「テキスト$${x_1}$$」「プレゼン$${x_2}$$」「ペース$${x_3}$$」「講師対処$${x_4}$$」の背後に「講師の質$${f_1}$$」という潜在変数を、「満足度$${x_5}$$」「理解度$${x_6}$$」「目的一致$${x_7}$$」の背後に「充実感$${f_2}$$」という潜在変数を仮定することにします。

分析用データ（X）はこのままでもよいのですが、後でsemopyでモデル表現する際の利便性を高めるため、列名を変更しておきましょう。

# 列名の変更

X.columns = ['x1', 'x2', 'x3', 'x4', 'x5', 'x6', 'x7']
X.head()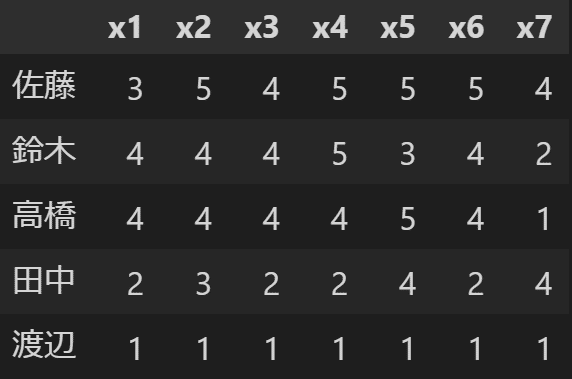

モデルの表現

上記でも述べたように、今回は講師の質$${f_1}$$という潜在変数から充実感$${f_2}$$という潜在変数への影響関係を仮定するモデルを構築してみましょう。パス図は以下のようになります。

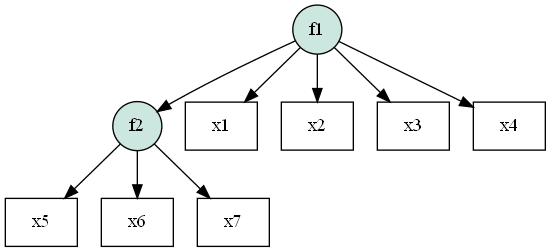
このモデルをsemopyのシンタックスに合わせて記述していきます。スクリプトは以下のようになります。

# モデル表現

mod = """
        f1 =~ x1 + x2 + x3 + x4
        f2 =~ x5 + x6 + x7
        f2 ~ f1
      """

ここで、semopyのシンタックスのうち、必ず覚えておかなければならない記号の紹介をしましょう。

=~：測定方程式を表現
~：構造方程式を表現
~~：共変関係を表現

測定方程式は、構成概念が観測変数に与える影響を表現する方程式です。「=~」はこの測定方程式を表現するための記号（Measurement operator）で、「=~」の左側に構成概念を、右側に観測変数を配置します。観測変数が複数ある場合は「+」記号でつなげて書くことが可能です。例. f1 =~ x1 + x2 + x3 + x4

構造方程式は、変数間の影響関係を表す方程式です。「~」はこの構造方程式を表現するための記号（Regression operator）で、「~」の左側に影響を与えられる変数（パス図の矢印が刺さる方）を、右側に影響を与える変数（パス図の矢印を出す方）を配置します。今回の場合だと、$${f_1}$$から$${f_2}$$に矢印が出ていますので「f2 ~ f1」のように表現します。また影響を与える変数が複数ある場合は、測定方程式と同じく「+」記号でつなげて書くことが可能です。

共変関係を表す記号「~~」は、モデルにおいて2変数間に共分散を仮定したい場合に指定します。ただし、外生的な構造変数には自動的に共変関係が設定されますので、特にモデル表現で明示的に書く必要はありません。それ以外の、例えば誤差変数間に共分散を仮定したい場合や特定の共分散を0に固定する場合などに利用することになります。

分析の実行

それでは分析を行いましょう。手順としてはモデルのインスタンスを作り、fit()メソッドで母数の推定を行います。スクリプトは以下のようになります。

# 分析の実行

model = semopy.Model(mod)
result = model.fit(data=X, obj='MLW')
print(result)

Name of objective: MLW
Optimization method: SLSQP
Optimization successful.
Optimization terminated successfully
Objective value: 0.127
Number of iterations: 32
Params: 2.249 1.550 1.857 0.569 0.385 1.287 1.463 0.275 0.942 1.160 1.126 0.689 0.905 0.716 0.107

fit()メソッドにおいて、「data=」の引数で分析する素データを指定します。もし共分散行列や相関行列から母数の推定を行いたい場合は「data=」の代わりに「cov=」を利用します。

「obj=」ではさまざまな推定方法を設定できます。今回はMLWを指定しています。これはウィッシャート最尤推定法で、デフォルトではこれが選択されています。ウィッシャート最尤推定は多変量正規分布の最尤推定の条件を緩めた推定法で、通常はこの推定法を選択するとよいでしょう。なお、2023年4月時点で、semopyで選択できる推定法は以下となります。

"MLW" （デフォルト）：ウィッシャート最尤推定法
"ULS"：重みなし最小2乗法。標本数が少ない場合でも推定値を得ることができますが、MLWより明らかに精度が劣っているため、できる限り利用は避けるのが無難です。
"GLS"：一般化最小2乗法。現在ではあまり積極的に利用するような場面はありません。
"WLS"：重み付き最小2乗法(ADF法としても知られています)。ADFは、重みの成分をデータの4次の積率を考慮して決定する方法で、変数が多変量正規分布に従っているという条件が満たされない場合でも正しい推定値を得られるという特徴があります。したがってMLWではうまく推定できない非正規データを扱う場合に選択できますが、最低でも数千単位の標本が必要となることに注意してください。
"DWLS"：対角重み付き最小2乗法（ロバストなWLSとしても知られています）。多変量正規分布に従わないようなデータに対して正しい推定結果を得ることができます。したがって、データに連続変数ではない観測変数が含まれている場合や、連続変数ではあるものの歪んだ分布をしているような変数が含まれている場合に選択することが推奨されます。
"FIML"：完全情報最尤推定法（データに欠損値がない場合、FIML は実質的に多変量正規分布を仮定した最尤推定法となります）。データに欠損値がある場合に選択するとよいでしょう。

結果の出力

結果の出力にはinspect()メソッドを利用します。標準化解まで求めたいことがほとんどだと思いますので、引数で「std_est=True」を指定しましょう。デフォルトではFalseになっています。

# 結果の出力

inspect = semopy.Model.inspect(model, std_est=True)
print(inspect)

   lval  op rval  Estimate  Est. Std  Std. Err   z-value   p-value
0    f2   ~   f1  1.287232  0.452642  0.596302  2.158691  0.030874
1    x1   ~   f1  1.000000  0.319421         -         -         -
2    x2   ~   f1  2.248801  0.814580   0.83806  2.683341  0.007289
3    x3   ~   f1  1.549738  0.425919   0.61482  2.520637  0.011714
4    x4   ~   f1  1.856697  0.538310  0.680838  2.727077   0.00639
5    x5   ~   f2  1.000000  0.659283         -         -         -
6    x6   ~   f2  0.569482  0.401297  0.249676  2.280888  0.022555
7    x7   ~   f2  0.385241  0.390219  0.170475  2.259813  0.023833
8    f2  ~~   f2  0.688562  0.795115  0.369775  1.862109  0.062588
9    f1  ~~   f1  0.107080  1.000000  0.071197  1.503999  0.132582
10   x7  ~~   x7  0.715512  0.847729  0.110703  6.463342       0.0
11   x3  ~~   x3  1.160482  0.818593  0.167434  6.930986       0.0
12   x4  ~~   x4  0.904733  0.710222  0.149385  6.056384       0.0
13   x6  ~~   x6  1.463128  0.838961  0.229864  6.365199       0.0
14   x5  ~~   x5  1.126378  0.565346  0.381447   2.95291  0.003148
15   x1  ~~   x1  0.942422  0.897971  0.128481  7.335107       0.0
16   x2  ~~   x2  0.274584  0.336459   0.13098  2.096377  0.036049

このように分析結果の基本的な情報が返されます。opの部分を見るとわかるように、構造方程式の部分も測定方程式の部分もなぜか「~」で表記されてしまっていることに注意してください。また分散と共分散は「~~」で表記されます。Estimateが非標準化解、Est. Stdが標準化解を表しています。

モデルの評価

SEMにおいてモデルを評価するには、適合度指標を利用します。また複数のモデルを比較して良し悪しを検討する際には情報量基準を利用します。これらの情報はcalc_stats()を使用することで求めることが可能です。

# 適合度の出力

stats = semopy.calc_stats(model)
print(stats.T)

                   Value
DoF            13.000000
DoF Baseline   21.000000
chi2           14.992196
chi2 p-value    0.307840
chi2 Baseline  92.893691
CFI             0.972290
GFI             0.838609
AGFI            0.739292
NFI             0.838609
TLI             0.955237
RMSEA           0.036191
AIC            29.745895
BIC            71.306164
LogLik          0.127053

上記の出力結果を見るとわかるように、重要な指標の1つであるSRMRが出力されないようです。いろいろ調べたのですが、semopyでは出力するためのメソッドは準備されていないようです。そこで、SRMRだけは別途自分で計算することにしましょう。定義式は以下となります。

$$
\text{SRMR} = \sqrt{\frac{2}{p(p + 1)} \sum_{i=1}^{n} \sum_{j=1}^{i} \left(r_{ij} - \hat{\rho}_{ij} \right)^2}
$$

ここで$${p}$$は変数の数、$${r_{ij}}$$は標本相関行列の第$${ij}$$要素、$${\hat{\rho}_{ij}}$$は母相関行列の第$${ij}$$要素$${\rho_{ij}}$$のモデルによる推定値です。

後はこの数式に従い、SRMRを計算すればよいだけなのですが、semopyの結果からは母共分散行列の推定値しかとりだせないので、共分散行列から相関行列へ変換する必要があります。そのため、factor_analyzerパッケージのutilsの中にcovariance_to_correlation()というメソッドがあるので、これを利用します。

それではSRMRを求めていきましょう。まずモデルの共分散行列を以下のようにして取得します。取得するためにcalc_sigma()を利用します。

# モデルの共分散行列の取得

model_matrix = semopy.Model.calc_sigma(model)
sigma = model_matrix[0]

そして、先ほど述べたcovariance_to_correlation()というメソッドを利用して相関行列へ変換します。

# モデルの共分散行列を相関行列に変換

rho = covariance_to_correlation(sigma)

次に標本相関行列を取得します。これは単純に素データから計算すればよいので、以下のようにします。

# 標本相関行列の取得

r = X.corr().to_numpy()

そして定義式に従い、以下のようにしてSRMRを算出します。

# SRMRの算出

p = r.shape[0]
A  = (r -rho) ** 2
num = (A.sum() - np.diag(A).sum()) / 2    
SRMR = np.power(2*num/(p*(p+1)), 0.5)
print(SRMR)

0.05603603938554767

結果は0.056となり、テキストP.34の表2.4のSRMRと一致していることがわかります。

構成概念スコア

因子分析を行った際に、各オブザベーションがどの程度その因子の特性を持っているかの尺度として、因子スコアというものがありました。SEMでも同様に、研究仮説として設定した潜在変数の特性を表す尺度として、構成概念スコアというものがあります。今回の「セミナーデータ」の場合、「講師の質」や「充実感」を、各セミナー参加者がどの程度持っているかを数値で表した尺度です。

semopyで構成概念スコアを推定するためには、predict_factors()を利用します。

# 構成概念スコアの推定

factor_score = semopy.Model.predict_factors(model, x=X)
print(factor_score)

           f1        f2
0    0.445810  1.612203
1    0.185856  0.266091
2    0.151901  0.689940
3   -0.325806  0.349024
4   -0.994854 -1.788295
..        ...       ...
113  0.185856  0.266091
114 -0.327294 -0.735919
115  0.289287 -0.359161
116  0.300843  0.163672
117  0.478441  1.508061

[118 rows x 2 columns]

この結果をわかりやすく散布図にプロットしてみましょう。横軸と縦軸のスケールは異なりますが、テキストP.38の図2.9と傾向は一致していることがわかります。

# 構成概念スコアの散布図のプロット

plt.xlim(-1.5, 1)
plt.ylim(-2, 2)
plt.title("構成概念スコアの散布図", fontsize=16)
plt.xlabel("講師の質", fontsize=12)
plt.ylabel("充実感", fontsize=12)
p = plt.scatter(factor_score.f1, factor_score.f2)
plt.show(p)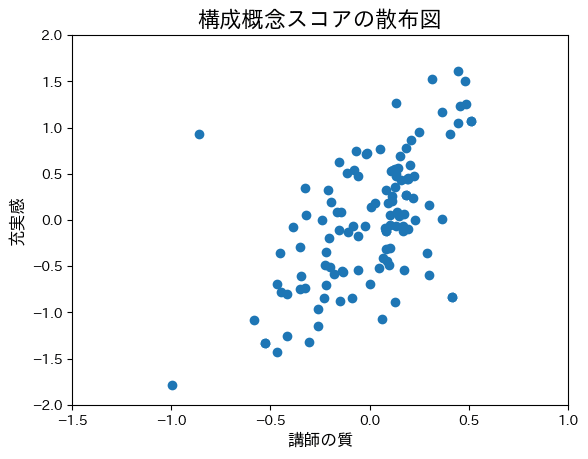

パス図の描画

最後にパス図の描画を行ってみましょう。semopyでも推定後のパス係数をつけてパス図を描画することが可能です。ただし、誤差変数に関しては描画することはできないので、もし論文等に掲載するための完全なパス図を描きたい場合は、別途作成しなおさないといけないことに注意しましょう。semopyでのパス図描画機能は、あくまで結果を確認するための簡易的な出力としての利用を想定しています。

# 推定後のパス係数付きパス図の出力

g = semopy.semplot(model, "model_est.png", plot_covs=True, std_ests=True, show=True)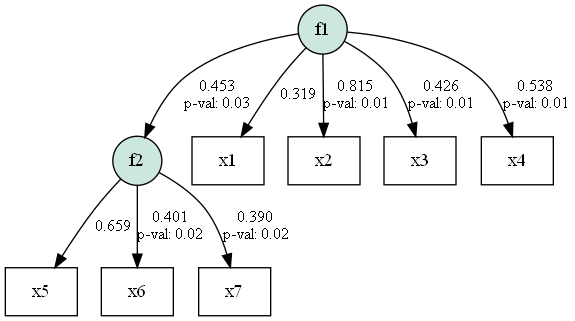

最後に

ちょっと長くなりましたが、SEMの分析の流れを一通りやってみました。このように簡単なモデルであれば、PythonでもRのlavaanと同様の結果が得られることがわかりました。

ただSEMの勉強をしたことがある方はご存じだと思いますが、SEMは恐ろしく柔軟な統計モデルで、さまざまな統計モデルを下位モデルに含むとともに、推定する母数に制約をかけたり、モデルに平均構造を入れたり、多母集団を同時に分析したりすることも可能です。このシリーズ（【Pythonで統計モデル】SEM編）では、semopyでこれらの分析が可能かどうか検証していきたいと思います。興味のある方はぜひフォローをお願いします！

今後の流れ

以下は掲載する予定の内容です。記事が出来次第、リンクを追加していきますが、調査の結果次第では削除するかもしれません。

母数に関する制約
パス解析（逐次モデル）
パス解析（非逐次モデル）
多変量回帰分析
MIMICモデル
PLSモデル
2次因子分析モデル、階層因子分析モデル
1因子分析モデルによる信頼性係数の推定
多特性多方法行列のための加法モデル
構成概念間の因果モデル
平均共分散構造分析
多母集団同時分析
潜在成長曲線モデル
ランダム効果

この記事が気に入ったらサポートをしてみませんか？