
確率分布を学ぶための基礎知識
当初は確率分布について扱おうと思っていたのですがかなり長くなってしまったので今回は基礎編とします。
以下の単語が説明できる際は不要です。
・確率密度関数(式の追加)
・累積分布関数(式の追加と説明の更新)
・確率変数
・歪度と尖度
・確率変数の期待値と分散(追記)
またこの記事ではCやPなどの入門は扱っていません。
・そもそもなぜ確率が必要なのか
よく書籍などで統計学の本を見ると確率とセットになることが多いと思います。また書いていなくても大抵確率とセットだと思います。
めちゃくちゃ簡単かつ大雑把に言うと、世の中が常にランダムネスに溢れているからです。人口を例にして見ると仮に1月1日に1000人生まれて12月31日に1000人亡くなり、その日以外では人は絶対に死なないと言う世界ならば人口の増減に関しての分析は必要ないと思います。でも実際は違いますよね。明日何人生まれて何人死ぬかなんて普通に過ごしていたら分からないですよね。ここで過去のデータ用いて一年後、10年後の人口は何人かを調べる際にはランダム性を考慮した分析が必要になってきます。
では簡単に確率が必要なのかと言うイメージが掴めたところで実際に深く入っていきます。最初に確率分布についてざっと説明します。
CやPなどの知識があることを前提に説明しています。(ある程度は説明は加えます。)
・確率分布とは
まず確率分布とはなんぞやと思うかもしれません。Wikipediaでは次のように説明されています。
確率分布(かくりつぶんぷ、英: probability distribution)は、確率変数に対して、各々の値をとる確率を表したものである。日本工業規格では、「確率変数がある値となる確率,又はある集合に属する確率を与える関数」と定義している[1]。
https://ja.m.wikipedia.org/wiki/%E7%A2%BA%E7%8E%87%E5%88%86%E5%B8%83
ランダムで動く変数(Xとする)の出方を表現したのが確率分布です。例としてサイコロを一個投げた際の確率分布を次のように表してます。こう言うのが確率分布です。上記の説明の確率変数とは各値に対してそれぞれ確率が与えられている変数のことを指します。下記の図ではサイコロの目を指します。
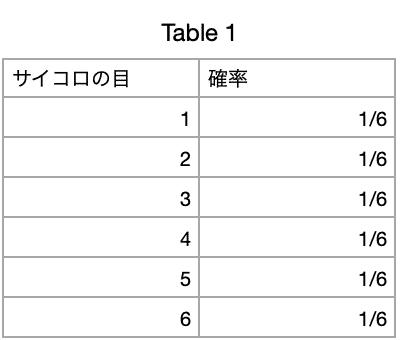
また確率変数には種類があります。それが今回詳しく述べる離散型と連続型です。離散型とはデータの間隔に意味があり0が一つの状態を指していることです。一方連続型とはデータの比率に意味があり、0が何もないことを指します。
0が一つの状態を指すと言う説明に納得がいかないかもしれませんが、具体例を挙げると双六のルーレットで0を出した際は何も起きていないかもしれませんが、実際には0進んだと捉えることができます。
一方連続型の場合身長0センチメートルと言われてもあんまりしっくりこないと思います。なぜなら存在しないからです。
値を0にした時説明できるかどうかの違いです。
次に確率を語る上では避けては通れない確率密度関数と累積分布関数について紹介します。
・確率密度関数
まず確率密度関数からです。では問題です。身長165cmの人の割合はどれくらいでしょうか。
正解は0人です。なぜかと言うと連続型の数値の際に165cmぴったりの人は恐らくいないです。実際には165.84829202...cmのようにいくらでも小さく見ることができます。一方離散型の数値の際には、先程のサイコロのようにある一点の確率は求めることができます。
ではある身長の確率を求める際にはどうしたら良いでしょうか。ここで登場するのが確率密度関数です。確率密度関数ではデータの範囲を用います。では身長165cmから170cmの人の割合はどのくらいですか。
これなら答えられそうですね。
割合を求める際には積分を使用して解きます。全体の面積を1として特定の範囲の面積を求めます。0.3だったら30%と言う感じです。
確率密度関数は一般的に連続型の値に使用されることが多いですが、離散型の値にも使うことができます。連続型の確率密度関数と離散型の確率密度関数の違いとして先程も述べましたが、離散型はある一点を取る確率は存在しますが連続型では存在しません。連続型では一点を用いる代わりにある範囲を確率としています。
・確率密度関数

上記の関数f(x)を確率密度関数と言います。
・累積分布関数
次に累積分布関数です。こちらはある値以下の確率を知りたい時に使用します。例えばサイコロを3回振った時に3の倍数が出る確率を求めたいとします。それぞれの結果は次のようになります。
・3の倍数が0回の確率は8/27
・3の倍数が1回の確率は4/9
・3の倍数が2回の確率は2/9
・3の倍数が3回の確率は1/27
となります。この結果を踏まえて、
・3の倍数が0回以下の確率は8/27
・3の倍数が1回以下の確率は20/27(8/27+4/9)
・3の倍数が2回以下の確率は26/27(8/27+4/9+2/9)
・3の倍数が3回以下の確率は27/27(8/27+4/9+2/9+1/27)
となり徐々に1に近づいていくのが分かります。これをプロットしたのが累積分布関数です。
連続型の累積分布関数の場合は左のようになり、離散型の累積分布関数場合は右のようになります。連続型、離散型の確率分布の代表的な例として指数分布と一様分布を取りあげます。指数分布と一様分布は後に扱います。

最後に累積分布関数の式を紹介します。F(x)を再度微分してあげれば密度関数が復元されます。例えばサイコロの目が4以下になる確率などを求める時に使用します。

・歪度と尖度
最後に歪度と尖度について紹介します。多分ほとんどの人が初めて聞いたと思います。
歪度とは分布が右もしくは左にどれくらい偏っているかを示す指標です。一方尖度とは分布の中心がどれくらい尖っているかを示しています。
まず歪度を見てみます。様々な分布を見てみるとどれも左右対称ではなく非対称だと思います。歪度は次のように表すことができます。Eが期待値(平均)、μも平均値でσが標準偏差です。Xーμは平均からどれくらい離れているかを示しています。これを計算してαが0以上なら右に歪んでいて、αが0以下なら左に歪んでいることを示していてこのαの値が大きいほど歪んでいると言うことです。大体の場合は分布を見ればわかると思いますが、似ている分布があった際には使えるかもしれません。(汚いですが手書きの方が早かったので許してください)

次に尖度です。尖度は先程の歪度の式を3乗から4乗に変えるだけです。この尖度は正規分布のα=3と比較してみることができます。正規分布とは平均0標準偏差が1の分布のことです。3よりも小さい場合は正規分布より鈍い形をしていて、大きい場合は正規分布より尖っていることを表しています。よくβ=α−3と表記されることがあります。
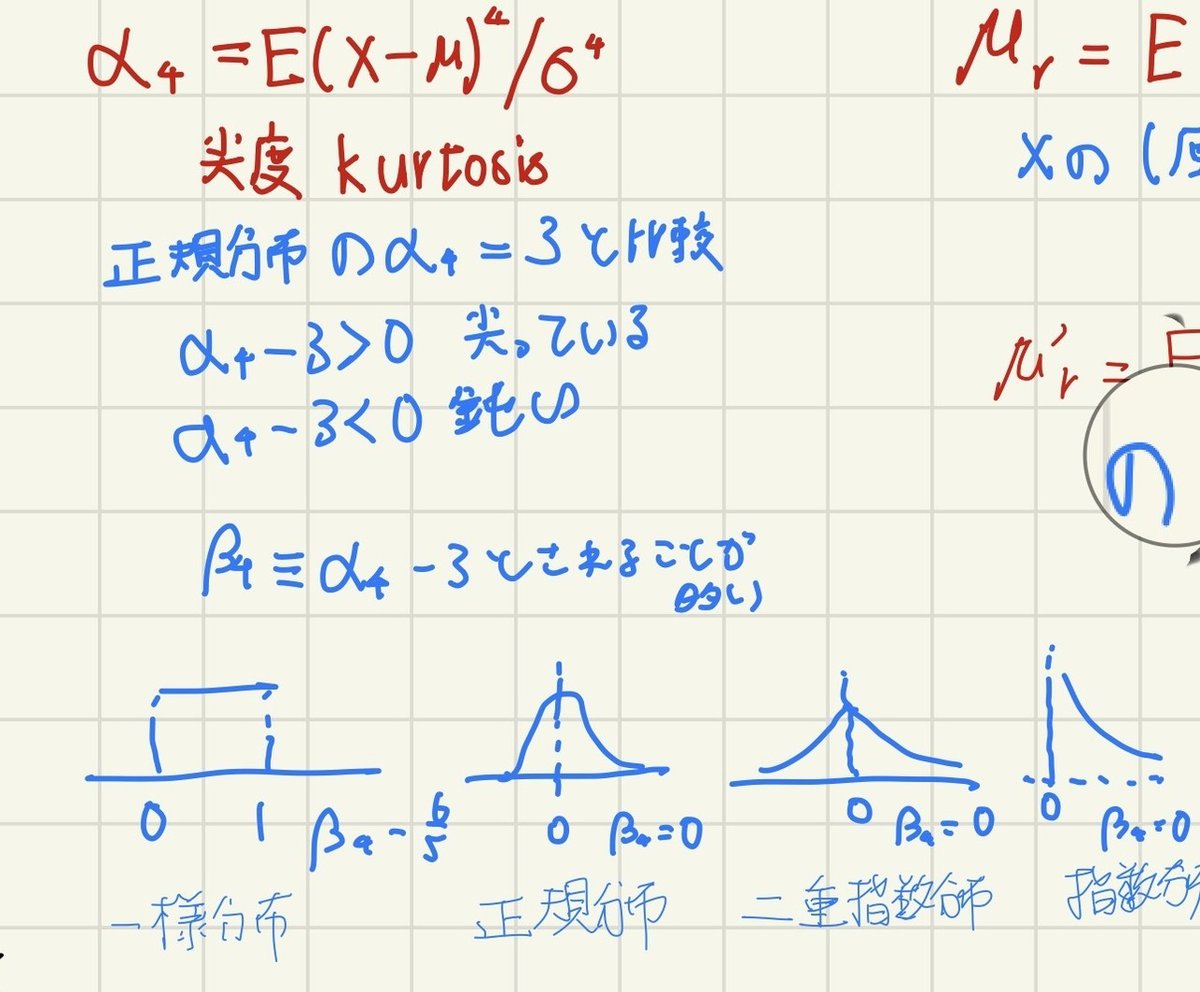
・確率変数の期待値と分散(追記)
期待値とは平均と似ているように見ますが着眼点が違います。平均は観測値全体から得た値ですが、期待値は試行それぞれの値です。
期待値の求め方は確率変数が離散型か連続型で異なってきます。ではまず離散型から紹介します。
・離散型の期待値
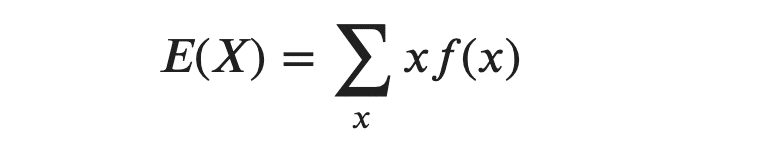
・連続型の期待値
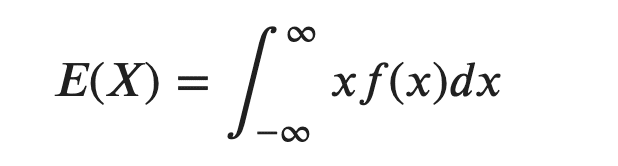
ここで期待値Eについての重要な性質を紹介します。
期待値の性質(Xを確率変数、cを定数とする)
・E(c)=c
・E(X+c)=E(X)+c
・E(cX)=cE(X)
・E(X+Y)=E(X)+E(Y)
まず一つ目から説明します。定数なので言葉通り変化することがありません。例えば両面に同じ値(c)が書かれたコインを投げるとすると、どちらが出ようと期待値は変わりません。それ以外にも今あなたが現金を持っているとするとその現金は使ったり増やしたりしなければ、所持金額は変わりません。
次に二つ目です。先程の現金を取り上げると変動しない所持金cにプラス宝くじを持っていたとします。この宝くじはもしかしたら一等の可能性もありますし三等、外れの可能性もあります。この宝くじ次第では所持金がプラスαになると言うことです。
次に三つ目です。ありえないかもしれませんが、同じ番号の宝くじを買った場合、当然期待値は買った枚数だけ倍々になります。もし買った宝くじが一等なら一等の賞金が二倍なります。(ないけど)
最後に四つ目です。これはさっきの三つ目とは少し違います。こちらの方が現実的かもしれません。違う番号の宝くじを買った際にはそれぞれの宝くじの期待値は違うため独立つまり、足算になります。
これで期待値の説明は終わります。次に分散の説明をします。ではまず文さんの定義からです。

定義上、上記の用に表現されるが実際に使用する際には次の等式を利用した方が計算がしやすくなります。

次に期待値と同様に分散にも重要な性質があります。
分散の重要な性質
・V(c)=0
・V(X+c)=V(X)
・V(cX)=c^2V(X)
これも先程の宝くじを例にあげて説明してみます。まず一つ目に関して、所持金額(定数)はどうあっても揺らぐことはありません。
次に二つ目です。宝くじを一枚買ったとしてその宝くじには一等から外れまでのばらつきが生じます。
最後に三つ目です。こちらは同じ番号の宝くじを買った場合、同様のばらつきが生じます。
これで確率の基礎知識が終了しました。次回から確率分布について扱います。
この記事が気に入ったらサポートをしてみませんか?
