
ベルの不等式の直観的理解—隠れた変数のモデルを大真面目に考えるー
はじめに
2022年のノーベル物理学賞は、ベルの不等式の破れを実証し、量子情報科学を開拓した業績で、アスペ、クラウザー、ツァイリンガーの3氏が受賞したのは記憶に新しい。20年前の大学院時代、私の博士論文の研究テーマが「陽子対のスピン相関の測定によるベルの不等式の検証」だったので、この分野の実験家からノーベル賞が出たのは感慨深いものがあった。ベルの不等式は、2つの系が量子論的にもつれた状態にあるときに、それらの観測量の相関が古典論では説明できないほど強くなる現象に絡むものである。その意味するところは非常に深いのだが、不等式の導出自体は驚くほど簡単で(高校数学レベル)、ベルの論文を初めて読んだとき、その慧眼に関心した覚えがある。しかし、ベルの不等式について教科書の解説や検証論文でよく出てくる表式は技巧的で、直観的に非常に分かりにくいのだ。本稿では、元実験物理屋の視点から、当時考えたベルの不等式の意味の直観的理解法について解説する。特に、いわゆる「隠れた変数」に基づいて色々なモデルを具体的に構成し、スピン相関に関して量子論との違いを可視化した例は珍しいと思う。いざ、量子論の奇妙な世界へGo!
※以下、予備知識は学部レベルの量子力学のみで可。
不等式が検証する「論点」
かのアインシュタインは、相対論の確立のみならず、量子論の土台建設にも多大な貢献をしたが、できあがった量子力学を一生涯認めず、現代物理学の主流から外れてしまったのはよく知られている。アインシュタインが反発したのは、人間が観測することで初めて物理状態が確定するという、量子力学特有の奇妙な性質に対してである。
例えば、スピン1/2の2粒子が、角運動量0にカップルした1重項状態$${^1S_0}$$にある場合、2粒子のスピンの状態ベクトルは、
$${\displaystyle |^1S_0>\;= \frac{1}{\sqrt{2}}\left( |\uparrow> |\downarrow>-\;|\downarrow>|\uparrow> \right)}$$ 式1
のようにもつれた状態にある。この場合、人間が観測する前においては、2粒子それぞれのスピンの向きは、全く確定していない。実は特定の方向を向いていて(互いに逆向き)、単に観測前は人間が知らないだけ、というのではなく、物理的に完全に未確定とされる。ここに大きな論点がある。
A) 観測前でも状態は確定していて、単に人間が知らないだけ(なので、ある系に対する観測が、遠方にある別の系の観測結果に遠隔作用的に影響を及ぼすことはない)
B) 人間が観測するまでは、そもそも物理的に状態が確定していない(遠隔作用的に見える振る舞いもあり得る)
もし、これら2つの解釈のいずれを採用しても、観測結果をうまく再現できるのだったら、わざわざ奇妙な(B)の方を採用する必要はないではないか?普通に考えたら(A)でしょう、というのが、量子論登場前の自然な考え方である。解釈(A)の考え方を、「局所実在論」というらしい。解釈(A)の場合、観測前においても、物理状態は何らかの「変数」(いわゆる「隠れた変数」)で特徴付けられるはずで(上記の例ではスピンの方向を含む)、量子力学では、その「変数」があらわに出て来ないのだから、物理状態を正確に表現しきれていないのではないか?このような意味で、量子力学は不完全な理論であるとアインシュタインは主張した(不完全であると主張しただけで、別に間違っていると主張したわけではないことに注意)。
では、上記解釈(A)に基づいて、量子論のどんな観測結果も説明可能なのだろうか? (A), (B)のいずれが正しいかを、実験的に決着をつけることはできないか? それができること証明したのが、ベルの不等式である。
1粒子のスピンを観測する場合
ベルの不等式の意味を把握するために、いきなり不等式を提示するのではなく、ステップを踏んで思考実験してみよう。問題は、上記解釈(A)に立脚した場合に、量子論による観測結果をどこまで再現できるのか?である。
まず、スピン1/2の1つの粒子のスピンの向きを観測する状況を考える。スピンを測定する場合、測定器には必ず測定する方向(測定軸)がある。例えば、シュテルン=ゲルラッハ装置でスピンを磁気モーメントの向きで測定する場合、装置の磁場勾配の方向が測定軸となる。観測されるスピンの量は、測定軸と同じ向き(符号$${+1}$$とする)か逆向き($${-1}$$とする)の2通りに限られる。
今、ベクトル$${\bold a}$$の方向の測定軸を持つ測定器に粒子を入射して、粒子のスピンの方向を観測する状況を考える(下図)。ここで、上記(A)の解釈に立脚して、観測前に粒子のスピンの向きは決まっているとしよう。観測前のスピンの向きをベクトル$${\bold s}$$で表し、ベクトル$${\bold a}$$, $${\bold s}$$のなす角を$${\theta}$$で表す。

このとき、この測定器で観測値$${+1}$$(ベクトル$${\bold a}$$と同方向)が得られる確率は、$${\theta}$$の関数で書けるはずである。それを$${f(\theta)}$$で表すとして、その関数形はどうあるべきだろうか?
量子力学でも、測定前にスピンの向きが決まっている場合を考えることはできる。量子力学の場合、上記$${f(\theta)}$$は、
$${\displaystyle f_{\text{QM}}(\theta)=\cos^2\frac{\theta}{2}\quad(-\pi\le\theta\le\pi)}$$ 式2
となる(下図)。

$${\theta = 0}$$(スピンが測定軸と同方向)の場合は$${f_{\text{QM}}=1}$$となり、必ず$${+1}$$が観測され、$${\theta = \pi}$$(スピンが測定軸と逆方向)の場合は$${f_{\text{QM}}=-1}$$となり、必ず$${-1}$$が観測される。中間の$${\theta = \pi/2}$$の時は、$${f_{\text{QM}}=1/2}$$となり、$${+1}$$と$${-1}$$が等確率で観測される。これら3値の$${\theta}$$の間の$${f_{\text{QM}}}$$はコサインの関数形でつながるわけである。
というわけで、解釈(A)に立脚した場合の$${f(\theta)}$$は、量子力学の場合を再現するように$${f(\theta)=f_{\text{QM}}(\theta)}$$と設定すべきだろう。また、解釈(A)に立脚する場合、観測値が確率的に決まるのは気持ち悪いので、粒子は、観測前に$${0\le \lambda \le 1}$$の範囲を一様分布する粒子固有のパラメータ$${\lambda}$$を持っているとする。この$${\lambda}$$を用いて、
(モデル1)
$${0 \le \lambda \le f_{\text{QM}}(\theta)}$$のとき、観測値は$${+1}$$
$${f_{\text{QM}}(\theta) \le \lambda \le 1}$$のとき、観測値は$${-1}$$
とする。
2粒子のスピン相関を観測する場合
さて、本題はここからである。今度は、2粒子のスピン相関を観測する場合を考える。式1のスピン1重項状態に組んでいる2粒子があり、それら2粒子のスピンの符号を、それぞれ別の測定器で測定する状況を考える。粒子1, 2に対応する測定器の測定軸の方向をそれぞれベクトル$${\bold a}$$, $${\bold b}$$とする。$${\bold a}$$, $${\bold b}$$のなす角を$${\Phi}$$とする(下図)。

このとき、量子力学によると、いずれの測定器においても、観測されるスピンの符号は$${+1}$$と$${-1}$$が等確率にランダムに現れるが、粒子対ごとに、2つの測定器で観測されるスピンの符号の積の期待値を求めると、そこに明瞭な相関が現れる。この、符号の積の期待値を$${C(\Phi)}$$で表すと、量子力学では、
$${C_\text{QM}(\Phi) =\,\, <{^1S}_0|(\sigma_1\cdot\bold a)(\sigma_2 \cdot \bold b)|^1S_0>\; = -\bold a\cdot\bold b = -\cos\Phi}$$ 式3
となる($${\sigma_1}$$, $${\sigma_2}$$はそれぞれ粒子1, 2のパウリ行列)。

上図に示したように、$${\bold a}$$, $${\bold b}$$が同方向($${\Phi = 0}$$)の場合、符号の積は常に$${-1}$$となり、$${\bold a}$$, $${\bold b}$$が逆方向($${\Phi = \pi}$$)の場合、符号の積は常に$${+1}$$となり、$${\bold a}$$, $${\bold b}$$が直角($${\Phi = \pi/2}$$)の場合、完全に無相関でゼロになる。これら$${\Phi}$$の3値における振る舞いは、直観的にも分かりやすいだろう。興味深いのは、これらの中間の$${\Phi}$$における振る舞いで、量子力学では、$${C_\text{QM}(\Phi)}$$はコサインの関数形でつながるわけである。
では、解釈(A)に立脚したモデルでスピン相関関数$${C(\Phi)}$$を求めたとき、量子力学の結果を再現、すなわち、
$${C(\Phi) = C_\text{QM}(\Phi)}$$
とすることができるだろうか?
ここからしばらく、この思考実験を考えてみよう。
モデル1の場合
まず、上述のモデル1を2粒子系に応用してみよう。スピン1重項状態とは、2粒子のスピンが互いに逆向きに組んで、合成角運動量がゼロになっている状態と考えられるので、観測前の2粒子のスピンは互いに逆向きに組んでいると考えればよさそうである。以下で、粒子1の測定器の向き$${\bold a}$$を基準にして、粒子2の測定器の向き$${\bold b}$$を、ある平面内で回転できるものとする。また、話を簡単にするために、観測前のスピンの向きも同じ面内に制限されるとする。観測前の粒子1, 2のスピンの向きを、それぞれ$${\theta}$$, $${\theta+\pi}$$で表す(下図)。
観測前に$${\theta}$$は$${-\pi\le\theta\le\pi}$$の範囲で一様に分布しているとする。また、観測されるスピンの符号を決めるパラメータ$${\lambda}$$は、粒子1, 2それぞれ$${\lambda_1}$$, $${\lambda_2}$$を独立に持っているとする。

軸aをy軸方向にとる。2つの測定軸と、観測前の2粒子のスピンの向きはすべてxy平面内に制限されるものとする。
この条件下で、スピン相関関数$${C(\Phi)}$$の具体的な表式を求めよう。$${C(\Phi)}$$は、スピンの符号の積の期待値であるから、粒子1, 2の観測値のペアが$${(+-)}$$となる確率を$${p_{+-}}$$などと表すことにすると、
$${C(\Phi)\equiv p_{++} + p_{--} - p_{+-} - p_{-+}}$$ 式4
と書ける。観測前の粒子1, 2のスピンの向きがそれぞれ$${\theta}$$, $${\theta+\pi}$$であるとき、
粒子1は、確率$${f(\theta)}$$で観測値$${+1}$$, 確率$${1-f(\theta)}$$で観測値$${-1}$$
粒子2は、確率$${f(\theta-\Phi)}$$で観測値$${-1}$$, 確率$${1-f(\theta-\Phi)}$$で観測値$${+1}$$
となる。これらを踏まえると、上記の4つの確率は以下のように書ける。
$${\displaystyle p_{++} = \frac{1}{2\pi}\int_{-\pi}^\pi f(\theta)\{ 1 - f(\theta-\Phi)\}d\theta}$$
$${\displaystyle p_{--} = \frac{1}{2\pi}\int_{-\pi}^\pi \{1-f(\theta)\}f(\theta-\Phi)d\theta}$$
$${\displaystyle p_{+-} = \frac{1}{2\pi}\int_{-\pi}^\pi f(\theta)f(\theta-\Phi)d\theta}$$
$${\displaystyle p_{-+} = \frac{1}{2\pi}\int_{-\pi}^\pi \{1-f(\theta)\}\{1-f(\theta-\Phi)\}d\theta}$$
これらを式4に代入して整理すると、
$${\displaystyle C(\Phi) = 1-\frac{1}{2\pi}\int_{-\pi}^\pi f(\theta)f(\theta-\Phi)d\theta}$$ 式5
となる。これが、モデル1の場合のスピン相関関数の表式である。
では、$${f(\theta)}$$を$${f_\text{QM}(\theta) = \cos^2(\theta/2)}$$に置き換えて式5を計算すると、量子力学の場合の式3を再現できるだろうか? 残念ながらそうはならず、
$${\displaystyle C(\Phi) = -\frac{1}{2}\cos\Phi}$$ 式6
となる(下図)。何と、量子力学の場合と比べて、相関の強さが半分に落ちてしまう。

※
今の場合、観測前のスピンの向きは図5に示した$${xy}$$平面内に制限したが、この制限を廃して3次元空間内で任意の方向をとれるようにした場合、式6の係数は$${1/3}$$になり、さらに相関が弱くなる。
階段関数の場合
量子力学で考えると、2つの測定軸が同方向($${\Phi = 0}$$)の場合、一方のスピンの符号の観測値が$${+1}$$ならば、他方の観測値は必ず$${-1}$$になるという、完全な相関を示す。ところが、解釈(A)に立脚したモデル1で考えると、この$${\Phi = 0}$$の場合の完全相関がいとも簡単に崩れてしまうのである。ではここで、1粒子のスピン観測で量子力学の結果を再現するという条件を外して、$${f(\theta)}$$として$${f_\text{QM}(\theta)}$$とは異なる関数も許した場合、どのような関数形にしたら$${C(\Phi=0) = -1}$$とできるだろうか? ちょっと考えると分かるが、
$${\displaystyle f(\theta) = \left\{\begin{array}{}1 & (|\theta| \le \pi/2)\quad\quad \\ 0 & (\pi/2 < |\theta| \le \pi) \end{array} \right.}$$ 式7
という階段関数にすると、スピン相関関数は、
$${\displaystyle C(\Phi) = \frac{2}{\pi}\Phi - 1}$$ 式8
という表式になり、$${C(\Phi=0) = -1}$$とすることができる(下図)。

が、式8は線形な関数であり、上図に示したように、$${0<\Phi<\pi/2}$$の範囲で量子力学の場合よりも相関が弱くなってしまうのである。
共通λモデル
何とかして、$${f(\theta) = f_\text{QM}(\theta)}$$の条件を満足しつつ、$${C(\Phi=0) = -1}$$とすることはできないか?というと、できないことはない。上記までのモデルでは、2粒子がそれぞれ持っているパラメータ$${\lambda_1}$$, $${\lambda_2}$$は互いに独立で何の相関もないと仮定していたが、それらに相関を持たせるモデルもあり得る。例えば、2粒子は共通の$${\lambda}$$を持っていることにして、それと、観測前のスピンの方向$${\theta}$$によって観測値が決まる、というモデルも考えられる。観測前は、2粒子はスピン1重項状態に組んでいるのだから、そのような仮定をおくのも不自然ではないだろう。
具体的には、少々技巧的だが、下図のように構成する。

$${\lambda}$$は$${0\le\lambda\le 1}$$の範囲を一様に分布しているとして、スピン1の符号は、$${(\lambda, \theta)}$$の座標によって上図に示したように決まるものとする。スピン2については、同じ$${\lambda}$$を用いて、角度は$${\theta+\pi-\Phi}$$として、符号を同じく上図から求める。
このモデルでスピン相関関数$${C(\Phi)}$$を計算するとどうなるか? 答えは、
$${\displaystyle C(\Phi) = -1 + \frac{2}{\pi}\Phi + \frac{4}{\pi}\left(\cos\Phi + \sin\frac{\Phi}{2} - \cos\frac{\Phi}{2} \right)}$$ 式9
となり、図示すると下図のようになる。

$${C(\Phi=0) = -1}$$は成り立つのだが、$${0<\Phi<\pi/2}$$の範囲で上弓なりに反ってしまい、上述の階段関数モデルの場合よりも相関が弱くなってしまう。この共通$${\lambda}$$モデルで、$${0<\Phi<\pi/2}$$の範囲の相関をもっと強くするには、$${f(\theta)}$$の非線形具合を線形にするしかなく、下図の場合に相関が最大になる。

しかし、この場合のスピン相関関数は結局式8と同じになってしまう。というわけで、$${\lambda}$$共通化の御利益はまったくないのである。
相関はどこまで大きくできるか?
では、もはや$${f(\theta) = f_\text{QM}(\theta)}$$の制約は忘れて、$${f(\theta)}$$の関数形として何でもありとした場合、$${C(\Phi)}$$の絶対値をどこまで大きくできるか?という問題を考えてみよう。$${f(\theta)}$$の関数形は、物理的な意味を考えると、最低限、以下の条件は必要である。
$${\displaystyle f(\theta) = f(-\theta)}$$ 式10(観測値は、測定軸とスピンの方向のなす角の絶対値で決まる)
$${\displaystyle f(\theta + 2\pi) = f(\theta)}$$ 式11(自明)
$${\displaystyle f\left(\frac{\pi}{2}-\theta\right) +f\left(\frac{\pi}{2}+\theta\right) = 1}$$ 式12($${\theta=\pi/2}$$を境界として反対称)
※
細かい話だが、スピンの測定にパリティ保存則を破る相互作用を利用する場合、式12は必ずしも成立しない。が、そのような測定系の場合、得られるスピン相関は無駄に弱くなるだけなので、今の場合は無視する。
単調減少関数を前提とすると?
$${f(\theta)}$$の物理的意味を考えると、$${0 \le \theta\le\pi/2}$$の範囲で単調減少関数を仮定するのが自然である。ところが、$${f(\theta)}$$が単調減少の場合、
$${\displaystyle C(\Phi) \ge \frac{2}{\pi} \Phi - 1 \quad \left( 0 \le \Phi \le \frac{\pi}{2}\right)}$$ 式13
となることが示される(補遺1参照)。階段関数の場合の相関(式8)を超えられないのである。
単調減少も無視すると?
もはや意地。では、$${f(\theta)}$$として不自然な関数形を仮定してもよいので、階段関数の相関を超えることはできるだろうか?? 答えは、できる。例えば、下図のような櫛(くし)形の$${f(\theta)}$$を仮定すると、、

$${C(\Phi)}$$は、下図のようになる。

$${\Phi = \pi/5}$$と$${\Phi = 2\pi/5}$$において、階段関数の限界どころか量子力学の限界も軽く超えて、完全相関$${|C| = 1}$$を示している。
では、$${f(\theta)}$$として下図のような櫛形を仮定して、段差の位置$${\theta_1}$$, $${\theta_2}$$を$${0\le\theta_1\le\theta_2\le\pi/2}$$の範囲でランダムに振った場合(外側の範囲では式10-12を満たすように延長する)、$${C(\Phi)}$$はどうなるでしょう?

数値計算で200パターンを生成して描いてみたのが下図である。
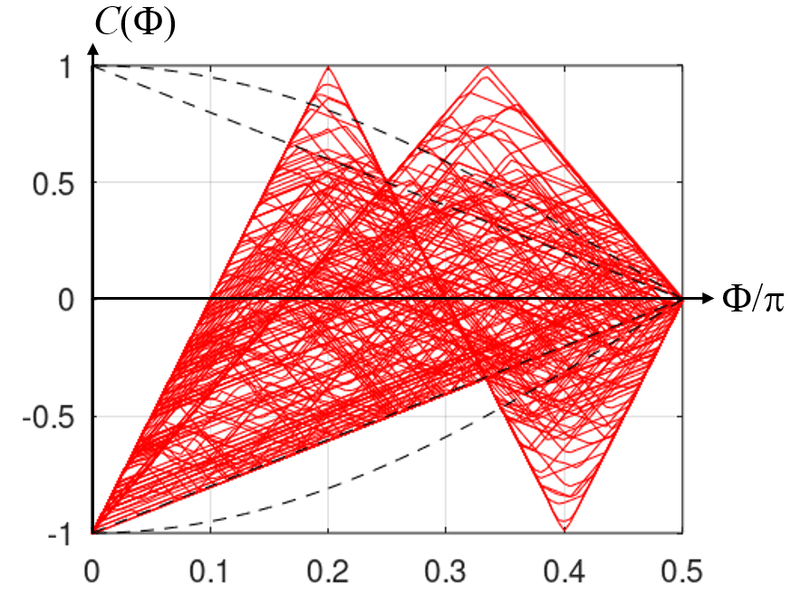
さらに、$${0\le\theta\le\pi/2}$$の範囲に櫛の歯をもう一本増やして、同様に櫛の歯の位置をランダムに振って500パターンを生成して描いたのが下図である。

多数の赤線の包絡線が、$${|C(\Phi)|}$$の上限を表す。これらを見ると、もはや、階段関数の限界値$${|C(\Phi)|\le|(2/\pi)\Phi-1|}$$は、$${|C(\Phi)|}$$に対して一般的な限界を与えるものではないことが一目瞭然だろう。しかし、例えば$${\Phi = \pi/4}$$(上のグラフの横軸で0.25の所)では、絶妙に$${|C(\Phi)| \le 1/2}$$の制限が掛かっているように見え、量子力学による値$${|C_\text{QM}(\pi/4)| = 1/\sqrt{2} \simeq 0.707}$$に到達するのは難しそうである。
超えられない壁=ベルの不等式
これまでの考察で見えてきたのは、冒頭に挙げた解釈(A)の局所実在論の考え方
系の物理状態は、観測前には、量子論ではあらわに見えない変数(「隠れた変数 hidden variables」)によって指定され、状態は確定している。
2つの系に対してそれぞれ測定を行う場合、一方に対する測定結果が、他方に対して遠隔的に影響を及ぼすことはない。
を前提とすると、スピン相関関数の絶対値$${|C(\Phi)|}$$にある上限がかかり、特定の$${\Phi}$$で量子力学の場合の相関を再現するのは無理そう、ということである。$${|C(\Phi)|}$$に対する上限は、図14, 15を眺めると分かるように、$${\Phi}$$関して凹凸のある関数となりそうだが、この上限をもっと単純な式で表せないだろうか? その表式を具体的に与えるのが、ベルの不等式である。
粒子1, 2のスピンの符号を、それぞれ測定軸$${\bold a}$$, $${\bold b}$$で測定したときのスピン相関関数を$${C(\bold a, \bold b)}$$で表すことにする。粒子1に対する測定軸として$${\bold a}$$と$${\bold a'}$$, 粒子2に対する測定軸として$${\bold b}$$と$${\bold b'}$$を用意したとき、局所実在論を前提とした場合、
$${S\equiv |C(\bold a, \bold b) - C(\bold a, \bold b')| + |C(\bold a', \bold b) + C(\bold a', \bold b')| \le 2}$$ 式14
の不等式が成り立つ、というのが、いわゆるベルの不等式(厳密には、Bell-CHSH不等式)の主張である。この不等式は、局所実在論に基づくモデルならば、どんなモデルでも成立する。本稿でこれまでに考えたモデルも局所実在論の範疇なので、式14が本当に成立するのか、見てみよう。
式14に現れる4つのベクトルがすべて同じ平面上にあるとして、引数のベクトル対がなす角をうまくとれば、式14は、
$${\displaystyle 2|C(\Phi)| + | C(\Phi) - C(3\Phi) | \le 2}$$ 式15
と書き直せる。ちょっと考えると分かるが、$${|C(\Phi)| \le 1}$$であることを考慮すると、上式は、$${S(\Phi) \equiv 3C(\Phi) - C(3\Phi)}$$として、
$${\displaystyle |S(\Phi) | \le 2}$$ 式16
と同値である。$${C(\Phi)}$$が求められていれば、$${S(\Phi)}$$に変換するのは簡単である。さて、図14, 15に示した$${C(\Phi)}$$を$${S(\Phi)}$$に変換するとどうなるか? 図示したのが下図である。
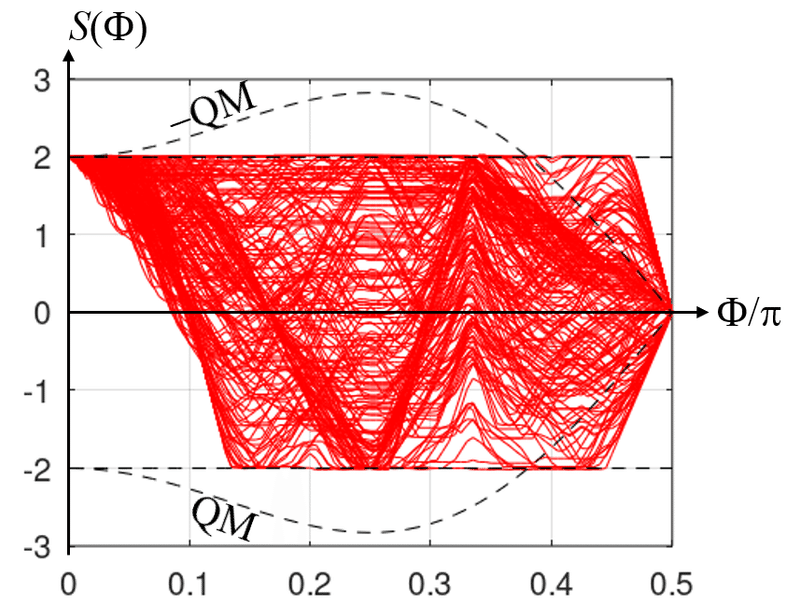

いずれも、見事に$${-2\le S(\Phi)\le2}$$の範囲に限定されるのが分かる!
一方、量子力学の場合の$${S(\Phi)}$$は、
$${S_\text{QM}(\Phi) = -3\cos\Phi+\cos3\Phi}$$ 式17
であり、上図に点線で示したように、$${0 < \Phi < \arccos\frac{\sqrt{3}-1}{2}\simeq 0.3807\pi}$$の範囲で$${|S_\text{QM}(\Phi)| > 2}$$となり、ベルの不等式を破る。特に、$${\Phi = \pi/4}$$で$${|S_\text{QM}(\pi/4)| = 2\sqrt{2}}$$の最大値をとる。
ベルの不等式の破れを示す論文は、この$${S(\Phi)}$$の形のスピン相関関数に変換した上で結果を示しているのがほとんどである。しかし、スピン相関の物理的な意味を考える場合、直接的な観測量はあくまで$${C(\Phi)}$$であり、$${S(\Phi)}$$よりも$${C(\Phi)}$$を用いる方が直観的にも考えやすいだろう。しかし残念ながら、ベルの不等式からは、$${|C(\Phi)|}$$に対しては離散的な$${\Phi}$$の値においてしか、上限値が得られないのである(補遺2参照)。
ベルの不等式から、局所実在論では
$${\displaystyle |C(\Phi)| \le |\frac{2}{\pi} \Phi - 1| \quad \left( 0 \le \Phi \le \frac{\pi}{2}\right)}$$ 式18
の不等式が連続な$${\Phi}$$で成り立つ旨の説明をたまに見かけるが、これまで議論してきたように、この形の不等式は、隠れた変数の任意のモデルで成り立つわけではない。上述のように、$${f(\theta)}$$が単調減少関数であるという、特殊な場合に限って成立する。話を簡単にするためにそう説明しているのならよいのだが、本当に誤解されているケースもありそうである。実際、冒頭に述べた通り、私は20年前ほど前に「陽子対のスピン相関の測定によるベルの不等式の検証」のテーマで学位を取得したのだが、博士論文審査の公聴会でこの辺の説明をしたら、副査に入っていた某理論系の先生(量子基礎論の専門家)から、「いや、そんなはずはないでしょう」と言われて驚いたことがある。上述のような技巧的なモデルを考えれば、ある範囲の$${\Phi}$$で式18を破るようなモデルは簡単に作れる旨を説明したら、それ以上の反論はなかったので、おそらく本当に誤解されていたらしい。小ネタではあるが、理論系の研究者も思いつかなかったようなことまで考察できていたことになるので、arXivにでも投稿しておいても良かった気がする。
まあともかく、ベルの不等式の評価に$${|C(\Phi)|}$$ではなく$${|S(\Phi)|}$$が使われる理由はこの辺にあるということ。
おわりに
以上、スピン相関関数の表現の2つの形式と、ベルの不等式との関係の話でした。これまで見てきたように、量子力学による結果はベルの不等式を破っており、またそれが繰り返し行われた多数の実験で実証されているので、自然法則の表現として、素朴な局所実在論を前提とするのは間違いなわけである。
では最後に、また思考実験。スピン1重項状態にある粒子対があり、粒子1, 2の順で、それぞれのスピンを個別に観測する状況を考える。このとき、先行する粒子1に対する観測が粒子2の状態に影響を及ぼすわけだが、この量子力学によるスピン相関の振る舞いをコンピュータでシミュレーションしようとするとき、粒子2の状態を確定させるためには、粒子1からどんな情報を送ればよいでしょう? 単純に考えると、粒子1が入射する測定器の軸の方向と、その方向に対して得た観測値(スピンの符号)の情報を送れば、粒子2は、送られてきたその方向に対して逆符号の状態に確定させることで、量子力学による振る舞いを再現することができる。
ところが、スピンの測定器に、そもそも測定軸がないケースもあるのだ。私が博士論文の研究で行った実験は、このケースに相当する。論文はこちら↓
H. Sakai, T. Saito, et. al., 2006. Spin Correlations of Strongly Interacting Massive Fermion Pairs as a Test of Bell's Inequality. Physical Review Letters, 97, 150405.
日本物理学会誌の和文解説記事はこちら↓
酒井英行・齋藤孝明, 2009. 陽子対を用いたベルの不等式の検証実験と非局所相関. 日本物理学会誌, 64(1): 33-37.
https://www.jps.or.jp/information/2022/10/04/64-1_33.pdf
この実験では、スピン1重項に組んでいる陽子対を炭素標的に入射し、2つの陽子それぞれの$${^{12}\text C}$$原子核からの散乱パターンを解析している。散乱の仕方の相関から、スピン相関関数を導出することができる。この実験の場合、測定器に相当するのは単なる炭素ブロックなので、測定軸のようなものは一切存在しない。さて、このタイプの測定方法の場合、2粒子間でどんな情報を送れば、量子力学のスピン相関を再現できるでしょう? 測定器に軸がある場合と比べて、本質的な違いはあるだろうか?
と、煙に巻いて、本稿を終わりにする。
補遺1. 式13の証明
$${f(\theta)}$$が単調減少関数である場合、$${0 \le \Phi \le \pi/2}$$の範囲で、
$${\displaystyle C(\Phi) \ge \frac{2}{\pi} \Phi - 1}$$ 式13再掲
が成立する。これを示すには、以下の3つの命題を示せば十分である。以下で、$${\Phi}$$の範囲は常に$${0 \le \Phi \le \pi/2}$$であり、$${f(\theta)}$$は式10-12を満たすものとする。また、$${f(\theta)}$$が単調減少関数であるというのは、$${0\le \theta \le \pi}$$の範囲における性質(式7の階段関数の場合も含む)とする。
i) $${C(0) = -1}$$となるのは、$${f(\theta)}$$が式7の階段関数のときのみである。
ii) $${\displaystyle C'(\Phi) \le 2/\pi}$$.
iii) $${ C'(\Phi) \ge 0}$$.
(i) の証明 $${C(\Phi)}$$の定義(式5)より、
$${\displaystyle C(0) = 1-\frac{2}{\pi}\int^\pi_{-\pi}\{f(\theta) \}^2 d\theta }$$
である。従って、$${C(0) = -1}$$とすると、
$${\displaystyle \int^\pi_{-\pi}\{f(\theta) \}^2 d\theta = \pi}$$
が成り立つ。一方、$${f(\theta)}$$の性質より、
$${\displaystyle \int^\pi_{-\pi}f(\theta) d\theta = \pi}$$
であるから、
$${\displaystyle \int^\pi_{-\pi}\{f(\theta) \}^2 d\theta = \int^\pi_{-\pi}f(\theta) d\theta}$$
が成り立たなければならない。$${0\le f(\theta)\le 1}$$の範囲をとる関数$${f(\theta)}$$で上式が成り立つのは、$${f(\theta)}$$の値が$${0, 1}$$に限られる階段関数の場合に限られる。■
(ii) の証明 $${C(\Phi)}$$の定義(式5)より、$${C(\Phi)}$$を微分すると、
$${\displaystyle C'(\Phi) = \frac{2}{\pi}\int^\pi_{-\pi}f(\theta)f'(\theta-\Phi)d\theta}$$.
ここで、$${f'(\theta-\Phi)}$$の関数形を考慮すると、$${-\pi + \Phi \le \theta \le \Phi}$$の範囲で$${f'(\theta-\Phi) \ge 0}$$であるので、
$${\displaystyle C'(\Phi) \le \frac{2}{\pi}\int^\Phi_{-\pi+\Phi}f(\theta)f'(\theta-\Phi)d\theta\\ \, \\ \quad\quad \le \frac{2}{\pi}\int^\Phi_{-\pi+\Phi}f'(\theta-\Phi)d\theta \\ \, \\ \quad\quad \le \frac{2}{\pi} \{f(0)-f(-\pi) \}\\ \, \\ \quad\quad \le \frac{2}{\pi}}$$. ■
(iii) の証明 $${C(\Phi)}$$の定義(式5)より、$${C(\Phi)}$$を微分すると、
$${\displaystyle C'(\Phi) = \frac{2}{\pi}\int^\pi_{-\pi}f(\theta)f'(\theta-\Phi)d\theta}$$.
部分積分を用いて、$${f(\pm\pi) = 0}$$とすると(今の場合、この仮定を置けば十分)、
$${\displaystyle C'(\Phi) = \frac{2}{\pi}\int^\pi_{-\pi}f'(\theta)f(\theta+\Phi)d\theta \\ \, \\ \quad \quad = \frac{2}{\pi}\int^0_{-\pi}f'(\theta)f(\theta+\Phi)d\theta + \frac{2}{\pi}\int^\pi_0f'(\theta)f(\theta+\Phi)d\theta }$$.
ここで、第2項の積分は、以下のように変形できる。
$${\displaystyle \int^\pi_0f'(\theta)f(\theta+\Phi)d\theta = \int^\pi_0 f'(\theta)f(-\theta-\Phi)d\theta\\ \, \\ \quad \quad = -\int_{-\pi}^0 f'(\theta)f(\theta-\Phi)d\theta}$$.
これを上式に代入すると、
$${\displaystyle C'(\Phi) = \frac{2}{\pi}\int^0_{-\pi}f'(\theta)\{f(\theta+\Phi)-f(\theta-\Phi) \}d\theta }$$.
ここで、$${-\pi\le\theta\le0}$$の範囲において、$${f'(\theta)\ge 0}$$かつ$${f(\theta+\Phi)-f(\theta-\Phi)\ge 0}$$であるから、
$${C'(\Phi) \ge 0}$$
が成り立つ。■
補遺2. 離散的なΦにおける|C(Φ)|の上限
Bell-CHSH不等式
$${S\equiv |C(\bold a, \bold b) - C(\bold a, \bold b')| + |C(\bold a', \bold b) + C(\bold a', \bold b')| \le 2}$$ 式14再掲
から、連続的な$${\Phi}$$に対して、$${|C(\Phi)|}$$に対する上限値を導出することはできないが、以下のような論法で、離散的な$${\Phi}$$に対して、$${|C(\Phi)|}$$の上限を導出することができる。上式に現れる4ベクトルがすべて同一平面上にあるとして、
$${\angle(\bold a', \bold a) = \alpha}$$,
$${\angle(\bold a, \bold b) = \Phi}$$,
$${\angle(\bold b, \bold b') = \beta}$$
とおくと、式14は、
$${\displaystyle |C(\Phi)-C(\Phi+\beta) | + |C(\Phi+\alpha+\beta)+C(\Phi+\alpha) | \le 2}$$ 式A1
となる。ここで、$${\alpha = 2\Phi}$$, $${\beta = \pi-2\Phi}$$と置き換えると、
$${\displaystyle |C(\Phi)-C(\pi-\Phi) | + |C(\pi+\Phi)+C(3\Phi) | \le 2}$$ 式A2
を得る。ここで、直接的な観測量であるスピン相関関数$${C(\Phi)}$$は、以下の性質を満たすべきである(スピン測定にパリティ保存則を破る相互作用を用いない限り、成立する)。
$${\displaystyle C\left(\frac{\pi}{2}-\Phi \right) = -C\left(\frac{\pi}{2}+\Phi \right)}$$ 式A3
$${\displaystyle C(-\Phi) = C(\Phi)}$$ 式A4
これらを用いると、式A2は、
$${\displaystyle |2(\Phi)|+|-C(\Phi)+C(3\Phi)| \le 2}$$
$${\displaystyle \therefore\; 2|(\Phi)|+|C(\Phi)|-|C(3\Phi)| \le 2}$$ 式A5
と変形できる。これより、
$${\displaystyle |C(\Phi)| \le \frac{1}{3}\left\{2+|C(3\Phi)| \right\}}$$ 式A6
を得る。ここで、$${\Phi = \pi/6}$$とすると、$${|C(\pi/2)| = 0}$$であるため、
$${\displaystyle |C\left(\frac{\pi}{6}\right)| \le \frac{2}{3}}$$ 式A7
を得る。次に、$${\Phi = \pi/(6\cdot3)}$$として、式A6, A7を用いると、
$${\displaystyle |C\left(\frac{\pi}{6\cdot 3}\right)| \le \frac{8}{9}}$$ 式A7
を得る。これを繰り返すと、
$${\Phi = \pi/6, \; \pi/(6\cdot 3), \; \pi/(6\cdot 3^2), \cdots}$$において、
$${\displaystyle |C(\Phi)| \le |\frac{2}{\pi}\Phi-1 |}$$ 式A8
が成り立つ。
また、式A1において$${\alpha = \Phi}$$, $${\beta = \pi-2\Phi}$$と置き換えて、まったく同様に考えると、$${\Phi = \pi/4, \; \pi/(4\cdot 2), \; \pi/(4\cdot 2^2), \cdots}$$において、式A8が成り立つことを示すことができる。
特に重要な値は、
$${|C(\pi/6)| \le 2/3}$$,
$${|C(\pi/4)| \le 1/2}$$
である。
図14, 15に、上記の$${|C(\Phi)|}$$の上限値を重ねてプロットしたのが、下図である。赤線の包絡線は、巧妙に青点を超えないのが分かる。


この、離散的な$${\Phi}$$における上限値を直接用いて、実測による不等式の破れを最初に提示したのは、私が知る限り、以下の論文である。
M. Lamehi-Rachti & W. Mittig, 1976. Quantum mechanics and hidden variables: A test of Bell's inequality by the measurement of the spin correlation in low-energy proton-proton scattering. Physical Review D, 14: 2543.
陽子対のスピン相関の測定で、私の実験の先行事例にあたる研究である。彼らは、下図に示したように、$${\Phi = 0, \pi/6, \pi/4, \pi/3, \pi/2}$$の5点で$${C(\Phi)}$$を測定しており、$${\Phi = \pi/6, \pi/4, \pi/3}$$の3点でベルの不等式の上限を破っているのを確認したという結果を提示している。

ここで注目すべきは、$${\Phi = \pi/3}$$(60°)における上限値を1/3 = 0.333に設定していることである。上述のように、$${\Phi = \pi/3}$$においては、$${|C(\Phi)|}$$に対する上限値は得ることができず、図A1を見ると、モデルによっては、$${|C(\pi/3)| = 1}$$の最大値もとることができる。何と彼らは、式A6からの式変形で計算を間違えたのでした(論文に導出過程も残っている)。以上、余談。
この記事が気に入ったらサポートをしてみませんか?
