
*007 解答
Q.7
10個の連続する奇数の合計が800となるとき、最も小さい数を求めなさい。
【解答】 71
地道に足して答えに導いていく方法もありますが、
それだと時間がかかる上、ミスも起きやすいです。
この場合はやっぱり公式を覚えておくのが得策。
誤解が無いように言うと、
「公式を覚える」
ただそれだけが大事なのではなく、
①公式を覚えるくらいまで問題を解くこと
②たとえ公式を忘れても導き出せること
この2つが問題を解くうえで非常に重要です。
数学だとなおさらです。
今回の問題の場合は
①等差数列の第n番目の数を求める公式
②等差数列の第n番目までの総和の公式
が分かっていないと非常に面倒な計算になりますので
そこから説明します。
まずは用語の説明から。
例えば3から始まる奇数が並んでいるとすると…

こんな感じで、となりの数は+2ずつ増えていきますよね。

この時のはじまりの数は「初項」といいます。
(項というのは、「番目」という意味です)
「最初の項(1番目)」だから初項。
ちなみに最後の項は「末項」と呼びます。
また、このように同じ数だけ増え続ける数列の場合、
となり合う2項間(例:3と5)の差のことを「公差」といいます。
小学生は「はじめの数(初項)」「となりの数の差(公差)」と呼んでいますが、長いのでこっちで覚えましょう。
次に、①等差数列の第n番目の数を求める公式を説明していきます。
例えば、3,5,7,9、〇と並んでいるときの
〇(第5番目)を求めましょう。
n=5の時ですね。

こういうことです。
「9+2」で解けちゃいますが、
あえて公式を使って解いてみましょう。

このように、初項3と、公差2×4回を足すと出てきます。
もし求めたい項が20番目なら3+(2×19回)、
50番目なら3+(2×49回)で求められます。
まとめると、

このように、第5番目は11ということが分かりました。
よって、

これで公式が導き出せました。
もしも公式を忘れたら、さっきみたいに具体的な数字で例を出して必ず「頭」ではなく「道筋」から思い出せるようにしましょう。
さて、次は②等差数列の第n番目までの総和の公式を導き出しますね。
さっきの数列の例でいきましょう。
総和とは、数列にある全ての数字を足したものです。

こういうことですね。
この後分かりやすくするために色をつけますね。

この数列を逆から順に並び替えて、下に書きます。
どういうことかというと…

こういうことです。
「並び替え」か「並べ替え」で迷って「並べ替え」にしました。
どうでもいいですね。
すると、こんなことが起こります。

実は並べ替えたものを下に書いて上下で足すと、
和が全て同じになるんです。
ちなみにこの数字14は、最初と最後の数字を足したもの、
すなわち「初項」と「末項」の和になると覚えてください。

14が5組で70になります。

勝手に同じ数列を足したので、
最後は2で割りましょう。
最初と最後の数字を足して、項数分(並んでいる数字の個数)だけ掛けて、最後に2で割る。
これを公式で表すと、

と、なります。
…はい、いよいよ問題の解説です!
そういえば「10個の連続する奇数の合計が800となるとき、最も小さい数を求めなさい」でしたね。
算数の基本ですが、求めたいものを〇と置いてしまう方が計算が楽になる場合が多いです。
10個の連続する奇数のうち、最も小さい数を〇とすると、最も大きい数はもう分かりますよね。

初項を〇とした時の末項は「〇+18」ということが分かりました。
次に、10個の連続する奇数の合計が800になることから、
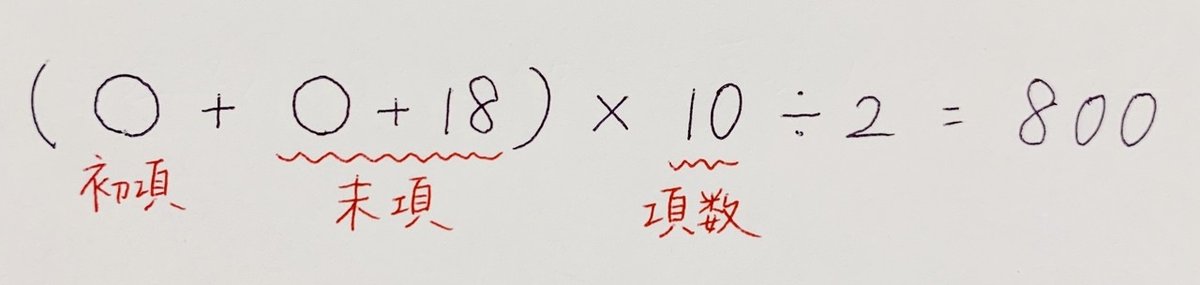
これを解けば、もう答えが目の前です。

よって、この数列は71から始まる数列(71,73,75,...,87,89)でした!
ここまでちゃんと読んだ人は間違いなく算数好きでしかない。
お疲れ様でした!
この記事が気に入ったらサポートをしてみませんか?
