
【数学】シュレディンガー方程式の極座標変換をするために偏微分を知ろう
先日アップしたシュレディンガー方程式の微分演算子∇^2の計算のNOTEではめちゃくちゃ偏微分の計算が出てきましたが、このNOTEは「偏微分ってそもそもどんなものなんですかいね?」っていうことをある程度理解しようというものです。
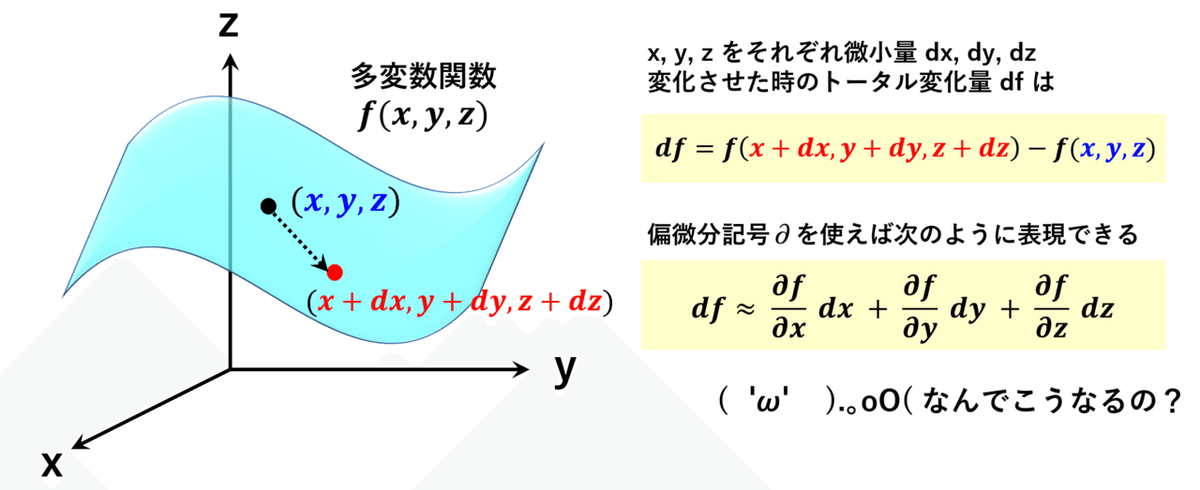
多変数関数、例えば3次元の関数 f 上のある点 (x, y ,z) から 点(x+dx, y+dy, z+dz) に移動した時の変化量 df はスライドのように2通りの書き方ができます。そのうちの1つは偏微分を用いて書き表すことができるんですけれど「どうしてこう書けるんや?」という理屈をこれから追ってみたいと思います。
式変形で見出す微分形

関数fの変化量 df は変化後の値 f (x+dx, y+dy, z+dz) から変化前の値 f (x, y ,z) を差し引けば求められます。この式に適当な関数値 ±f (x, y+dy, z+dz), ±f (x, y, z+dz)を導入します。同じ量を足し引きするので df の値は変わりません。すると x, y ,z それぞれの成分だけが変化したような3要素がでてきます(黄色塗り部分)。
次に、この3要素にそれぞれの微小成分を導入します。同じ量を掛けて割るので df の値は変わりません。式中の分数部分、緑で塗ったエリアは微分の定義式もどきになりました。
無限小領域と極限

この分数部分に注目して、無限小領域における変化量を考えてみましょう。スライド下の緑塗りエリアに書いたように、3要素のうち x, y の項の一部を dx, dy, dz ≈ 0 として元の式に放り込みます(根拠としては「dx, dy, dz は無限小領域の中で更に微分された極少量なんやから、x, y, z と比べたら無視できるほどちっちゃいし、別に0としても大して f の値は変わらんやろ?」という感じ)。
偏微分式の出現

こう式変形させてみると、分数部分は「関数fの2変数を固定させて、残りの1変数だけ変化させたで」っていう微分形となります。これがちょうど、1つの変数以外を定数とみなして微分する偏微分と同じ意味になります。
偏微分についていちいち極限を用いた表現で書くのが面倒くさいので、便宜上通常の微分記号dと区別して記号 ∂ を用いて最後の式のように略記します。スライドの黄色に塗ってるエリアが偏微分に相当する部分になります。そう見ると偏微分記号は便利ですよね。
シュレディンガー方程式での2階偏微分

シュレディンガー方程式では2階偏微分が大量にでてきます。例に挙げたのは ∂/∂x を r で偏微分(ほぼほぼ積の微分)している式です。
微分記号 ∂/∂r は「∂/∂r のすぐ後ろの関数を r で微分してやー」という指示なんですけれども、自分みたいに偏微分を良く分かってないと「 r と関係なさそうなこの ∂/∂θ・∂/∂φ っていうよく分からんやつ、見やすくなるしカッコ外に出しといたろ ٩( 'ω' )و」っていうイージーミスをやらかしてしまいます。
この微分記号をカッコ外に出す操作は、微分する順番や関数を自分勝手にいじくっているという意味なので、当然ながら計算結果が違ってくる可能性があるわけなんです。まぁ至極ナチュラルにこういう間違いをするということは、その程度しか偏微分を理解していないっていうことの裏返しなので、もし2階偏微分を計算する際は微分記号を無闇に移動させないことが大事だと言えますね。
「ためになるわ」と感じて頂ければサポートを頂ければ幸いです。よろしくお願いいたします。
