人口増加と人口減少はどちらが持続可能か?プログラミングと数学を用いて検証してみた!
はじめに
人口減少により、持続可能性が危ういということが言われる。しかし、地球上の資源の有限性を考慮すると、このことは必ずしも正しくない。むしろ、人口を徐々に減少させ、資源をゆっくりと消費していく方が、人類の持続可能な期間が伸びることも考えられる。そこで、このノートでは、簡単なシミュレーションと数学の計算により、人口増加と減少のどちらが持続可能性があるかを検証した。
考え方・前提
ここでは、人類は、次の1.または 2.のどれかに初めてなった年に絶滅するものとし、絶滅までの年数を人類存続可能年数という。
人類の人口が1人未満になる
地球上に存在する資源量が0以下になる。
一人当たり資源消費量は、経過年数にかかわらず同じとする。また、人口増加率も、経過年数にかかわらず同じとする。
資源は、消費されるとその分減少し、それ以外の理由により減少または増加することはないものとする。
初期(1年目のことをいう。以下同じ)に地球上にある資源量を、初期に人類が消費する資源量で割った値は、人口が一定の場合における人類存続可能年数から1を引いた数(以下人口一定時存続可能年数という)と同じである。このシミュレーションでは、人口一定時存続可能年数を、初期に地球上にある資源量の代わりに用いる。そして、人口一定時存続可能年数と人口増加率をそれぞれ変えていくと、人類存続可能年数がどのように変わるのかを調べる。
ある人口一定時存続可能年数のときに、人類存続可能年数が最大となるような人口増加率を、その人口一定時存続可能年数における最長存続可能人口増加率という。
初期の人類の人口は、80億人とする。
シミュレーション
方法
次のようなPythonプログラムを用いる。なお、実行に非常に時間がかかるため注意する。
import numpy as np
import matplotlib.pyplot as plt
# 人口増加率と人口一定時存続可能年数から人類存続可能年数を求める関数
# incrt:人口増加率、rsrc0perpop0:人口一定時存続可能年数
def extnctyear(incrt, rsrc0perpop0):
pop0 = 8e9 # 人類の初期人口80億人
rsrccnsmppercpt = 1 # 一人当たり資源消費量(1とする)
rsrc0 = pop0 * rsrc0perpop0 * rsrccnsmppercpt # 初期の資源量
pop = [pop0] # 各年の人口
rsrc = [rsrc0] # 各年の資源量
year = 0 # 年数
# 人口が1人より大きく、かつ、資源量が0より大きい間に
while pop[year] > 1 and 0 < rsrc[year]:
# 翌年の人口を求める
pop += [(1 + incrt) * pop[year]]
# 翌年の資源量を求める
rsrc += [rsrc[year] - rsrccnsmppercpt * pop[year]]
year += 1
return year + 1
incrts = np.arange(-0.999, 0.999, 0.001) # -0.999~0.999の人口増加率
rsrc0perpop0s = np.arange(100, 100000, 100) # 100~100000の
# 人口一定時存続可能年数
# 各人口増加率・各人口一定時存続可能年数における人類存続可能年数を求める
X, Y = np.meshgrid(incrts, rsrc0perpop0s)
Z = np.zeros((len(rsrc0perpop0s), len(incrts)))
for i in range(len(rsrc0perpop0s)):
for j in range(len(incrts)):
Z[i, j] = extnctyear(X[i, j], Y[i, j])
# 等高線図を作成
lvls = [1e0, 1e1, 2e1, 3e1, 4e1, 5e1, 7e1, 1e2, 2e2, 1e3]
cont = plt.contour(X, Y, Z, levels=lvls)
plt.colorbar(cont)
plt.title('人類存続可能年数', fontname="MS Gothic")
plt.xlabel('人口増加率', fontname="MS Gothic")
plt.ylabel('人口一定時存続可能年数', fontname="MS Gothic")
plt.show()
# 各人口増加率・各人口一定時存続可能年数における人類存続可能年数を求める
syear = [[extnctyear(incrts[j], rsrc0perpop0s[i]) for j in range(len(incrts))] \
for i in range(len(rsrc0perpop0s))]
# 各人口一定時存続可能年数における最長存続可能人口増加率を求める
MIRR = [incrts[_.index(max(_))] for _ in syear]
# プロットする
plt.plot(rsrc0perpop0s, MIRR)
plt.title('各人口一定時存続可能年数における最長存続可能人口増加率', \
fontname="MS Gothic")
plt.xlabel('人口一定時存続可能年数', fontname="MS Gothic")
plt.ylabel('最長存続可能人口増加率', fontname="MS Gothic")
plt.show()結果
次のような等高線図と線グラフが得られた。
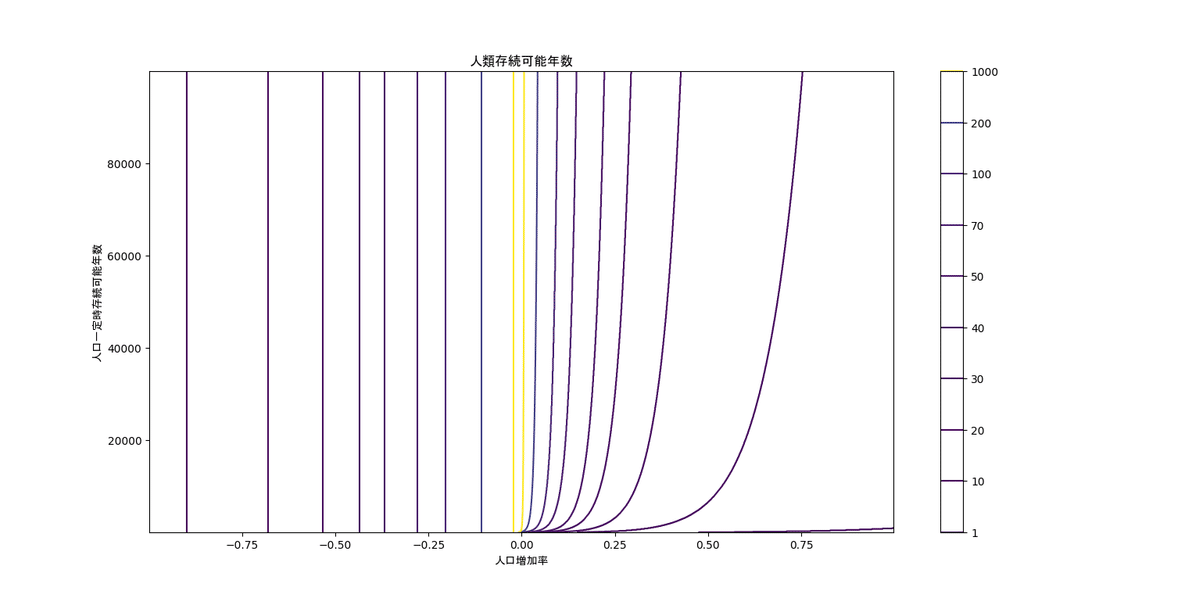

また、上記pythonプログラムの`incrts = np.arange(-0.999, 0.999, 0.001)`を`incrts = np.arange(-0.0999, 0.0999, 0.0001)`として人口増加率の範囲を-0.0999から0.0999までにして刻み幅を0.0001にし、また、`lvls = [1e0, 1e1, 2e1, 3e1, 4e1, 5e1, 7e1, 1e2, 2e2, 1e3]`として等高線を入れる値を変えた結果、次のような等高線図とグラフが得られた。


考察
等高線図をみると、左右の端に近づくほど(つまり人口増加率の絶対値が大きくなるほど)、人類存続可能年数が短くなっているが、左に向かう(つまり人口増加率が負で小さくなっていく)ほうが、右に向かう(つまり人口増加率が正で大きくなっていく)よりも、人類存続可能年数の減り方は穏やかであることが見て取れる。ただし、右上(つまり、人口増加率と人口一定時存続可能年数がともに非常に大きい)においては、左右反転させたときに対応する左上(つまり、人口増加率が非常に小さく、人口一定時存続可能年数が非常に大きい)よりも、人類存続可能年数が大きい。
また、左半分(つまり人口増加率が負)においては、等高線が縦軸に平行(つまり、人類存続可能年数は人口一定時存続可能年数に依存しない)であるのに対し、右半分(つまり人口増加率が正)においては、等高線が右斜め上に伸びている(つまり、人口一定時存続可能年数が大きいほど、人類存続可能年数も大きくなる)ことが分かる。
最長存続可能人口増加率のグラフを見ると、人口一定時存続可能年数が2万程度までは、最長存続可能人口増加率は負で、その他では0であるが、グラフ2を見ると、最長存続可能人口増加率はすべて負の値である。グラフでは人口増加率の刻み幅が0.001で、グラフ2の0.0001より解像度が低いため、このようなことが生じていると考えられ、実際は、最長存続可能人口増加率はすべて負の値になると思われる。
結論
人口増加と人口減少のどれが持続可能性があるかは、現在地球上にどのくらい資源があるのかと、増加または減少の程度による。しかし、増減の程度が穏やかで、かつ、現在の地球上にある資源では現在の地球人口を高々数万年程度しか養えないとする場合は、人口減少の方が持続可能性がある可能性が高い。また、人類の持続可能性が最も高くなるのは、人口が減少する場合である。
数学
上記では、シミュレーションを用いて人類存続可能年数と最長存続可能人口増加率を求めたが、以下では、これを数学的に求める。
$${y}$$年の地球人口を$${p_y}$$、同年の地球上の資源量(以下単に資源量という)を$${R_y}$$、一人当たり資源消費量を$${r}$$、人口一定時存続可能年数を$${Y=\frac{R_1}{rp_1}}$$、人類存続可能年数を$${y_\mathrm{s}}$$とおく。
また、複号同順とする。
人口および資源量の一般項
$${p_y}$$と$${R_y}$$の一般項を求める。
$${p_y}$$を漸化式で表すと、
$$
p_{y+1}=(1+i)p_y
$$
である。これの一般項は容易に求めることができ、
$$
p_y=(1+i)^{y-1}p_1
$$
となる。
資源量の漸化式は、
$$
R_{y+1}=R_y-rp_y
$$
であり、これに$${p_y}$$の一般項を代入すると、
$$
R_{y+1}=R_y-r(1+i)^{y-1}p_1
$$
となる。この両辺を$${(1+i)^{y+1}}$$で割ると、
$$
\frac{R_{y+1}}{(1+i)^{y+1}}=\frac{1}{1+i}\frac{R_y}{(1+i)^y}-\frac{rp_1}{(1+i)^2}
$$
である。ここで、$${a_y=\frac{R_y}{(1+i)^y}}$$とおくと、これは、
$$
a_{y+1}=\frac{1}{1+i}a_y-\frac{rp_1}{(1+i)^2}
$$
となる。これを変形すると、
$$
a_{y+1}+\frac{rp_1}{i(1+i)}=\frac{1}{1+i}\left(a_y+\frac{rp_1}{i(1+i)}\right)
$$
となり、ここで$${b_y=a_y+\frac{rp_1}{i(1+i)}}$$とおくと、これは
$$
b_{y+1}=\frac{1}{1+i}b_y
$$
となる。$${b_y}$$の一般項は、
$$
b_y=\left(\frac{1}{1+i}\right)^{y-1}b_1
$$
であり、これに$${b_y=a_y+\frac{rp_1}{i(1+i)}}$$を代入すると
$$
a_y+\frac{rp_1}{i(1+i)}=\left(\frac{1}{1+i}\right)^{y-1}\left(a_1+\frac{rp_1}{i(1+i)}\right)
$$
すなわち
$$
a_y=\left(\frac{1}{1+i}\right)^{y-1}\left(a_1+\frac{rp_1}{i(1+i)}\right)-\frac{rp_1}{i(1+i)}
$$
である。これに$${a_y=\frac{R_y}{(1+i)^y}}$$を代入すると
$$
\begin{align*}
\frac{R_y}{(1+i)^y}&=\left(\frac{1}{1+i}\right)^{y-1}\left(\frac{R_1}{(1+i)}+\frac{rp_1}{i(1+i)}\right)-\frac{rp_1}{i(1+i)} \\
&=\left(\frac{1}{1+i}\right)^y\left(R_1+\frac{rp_1}{i}\right)-\frac{rp_1}{i(1+i)}
\end{align*}
$$
すなわち
$$
\begin{align*}
R_y&=R_1+\frac{rp_1}{i}-\frac{rp_1(1+i)^{y-1}}{i}\\
&=R_1+\frac{rp_1}{i}\left(1-(1+i)^{y-1}\right)\\
&=R_1-\frac{rp_1}{i}\left((1+i)^{y-1}-1\right)
\end{align*}
$$
である。
人類存続可能年数
以上で求めた一般項から、人類存続可能年数を求める。
まず、1.(人口が1人未満になる)で人類が絶滅する場合を考える。
$$
\begin{align*}
p_y&<1\\
(1+i)^{y-1}p_1&<1\\
(1+i)^{y-1}&<\frac{1}{p_1}\\
y-1&<\log_{1+i}{\frac{1}{p_1}}\\
y&<\log_{1+i}{\frac{1}{p_1}}+1
\end{align*}
$$
なので、1.で人類が絶滅する場合の人類存続可能年数は、
$$
y_\mathrm{s}=\left\lceil\log_{1+i}{\frac{1}{p_1}}+1\right\rceil
$$
である。ここで、$${\frac{1}{p_1}<1,y_\mathrm{s}>1}$$であるため、$${1+i>1\iff i>0}$$すなわち人口増加のときは、1.で人類が絶滅することはない。これは、直感的に考えても当然のことである。
次に、2.(資源量が0以下になる)で人類が絶滅する場合を考える。
$$
\begin{align*}
R_y&<0\\
R_1-\frac{rp_1}{i}\left((1+i)^{y-1}-1\right)&<0\\
-\frac{rp_1}{i}\left((1+i)^{y-1}-1\right)&<-R_1\\
\frac{rp_1}{i}\left((1+i)^{y-1}-1\right)&>R_1\\
(1+i)^{y-1}-1&\gtrless \frac{i}{rp_1}R_1 & &i\gtrless 0\\
(1+i)^{y-1}&\gtrless iY+1 & &i\gtrless 0\\
y-1&>\log_{1+i}{(iY+1)}\\
y&>\log_{1+i}{(iY+1)}+1
\end{align*}
$$
であるから、2.で人類が絶滅する場合の人類存続可能年数は、
$$
y_\mathrm{s}=\left\lceil\log_{1+i}{(iY+1)}+1\right\rceil
$$
である。
$${iY+1<0 \iff i<-\frac{1}{Y}}$$のときは、負の数の対数は未定義であるから、2.で人類が絶滅することはない。
以上より、$${-\frac{1}{Y} < i < 0}$$のときは、1.と2.のどちらでも絶滅する可能性があることになるため、どちらが早いのかが問題となるが、
$$
\begin{align*}
\log_{1+i}{\frac{1}{p_1}}+1&\gtreqless \log_{1+i}{(iY+1)}+1\\
\frac{1}{p_1}&\lesseqgtr iY+1\\
iY&\gtreqless \frac{1}{p_1}-1\\
i&\gtreqless \frac{1}{Y}\left(\frac{1}{p_1}-1\right)
\end{align*}
$$
より、$${i= \frac{1}{Y}\left(\frac{1}{p_1}-1\right)}$$を境にどちらが早いのかが切り替わることがわかる。
以上をまとめると、人類存続可能年数は、次のようになる。
$$
y_\mathrm{s}=
\begin{cases}
\left\lceil\log_{1+i}{\frac{1}{p_1}}+1\right\rceil & i< -\frac{1}{Y}\left(1-\frac{1}{p_1}\right)\\
\left\lceil\log_{1+i}{(iY+1)}+1\right\rceil & -\frac{1}{Y}\left(1-\frac{1}{p_1}\right)\leq i<0\\
Y+1 & i=0 \\
\left\lceil\log_{1+i}{(iY+1)}+1\right\rceil & i>0
\end{cases}
$$
最長存続可能人口増加率
人口一定時存続可能年数$${Y}$$における最長存続可能人口増加率$${i_{\mathrm{m}}(Y)}$$を求める。
以下では次の事実を証明なしに用いる。
$${a>1}$$のとき、関数$${f(x)=\log_{1+x}{(1+ax)}}$$は単調減少する。
$${a\gtrless 1}$$のとき、$${x\gtrless \log_a x +1}$$である。
$${Y> 1}$$より、$${i\gtrless 0}$$のときは
$$
\begin{align*}
\log_{1+i}{(iY+1)}&\lessgtr \log_{1+i}{(iY+Y)}\\
&=\log_{1+i}{((1+i)Y)}\\
&=\log_{1+i}Y+1\\
&\lessgtr Y
\end{align*}
$$
である。したがって、$${ i\geq -\frac{1}{Y}\left(1-\frac{1}{p_1}\right)}$$の範囲においては、$${i=-\frac{1}{Y}\left(1-\frac{1}{p_1}\right)}$$のときに、$${y_\mathrm{s}}$$が最大となり、その値は
$$
\begin{align*}
\left\lceil\log_{1-\frac{1}{Y}\left(1-\frac{1}{p_1}\right)}{\left(-\frac{1}{Y}\left(1-\frac{1}{p_1}\right)Y+1\right)}+1\right\rceil\\
=\left\lceil\log_{1-\frac{1}{Y}\left(1-\frac{1}{p_1}\right)}{\frac{1}{p_1}}+1\right\rceil
\end{align*}
$$
である。$${i< -\frac{1}{Y}\left(1-\frac{1}{p_1}\right)}$$の場合でも、$${y_\mathrm{s}}$$はこれより大きくなることはない。以上より、最長存続可能人口増加率は
$$
i_{\mathrm{m}}(Y)=-\frac{1}{Y}\left(1-\frac{1}{p_1}\right)
$$
である。
結論
やはり、最長存続可能人口増加率は常に負になるようである。
まとめ
このノートでは、おおむね人口減少の方が持続可能性があり、また、最も持続可能性がある人口増加率は負であることを、プログラムと数式によって確かめた。なお、上記計算は、人口増加率が経過年数を問わず一定であることや、資源は減少するだけで回復しないことを前提として行ったものであるが、これらの前提がない場合はなおさら人口減少の方が持続可能性があることになる。なぜなら、人口増加率を各年ごとに変更できるような場合は、とりあえず人口を最低限まで減らし、それからその人口を維持するときに最も持続可能性があるし、また、一定の年数が経過すると資源が回復するような場合は、人口が減少させれば、資源が回復するまで人類を滅亡させずに待つようなことができるからである。
この記事が気に入ったらサポートをしてみませんか?
