
身の回りのこともx軸とy軸で説明しちゃう”4象限おじさん”
■なんでも4象限で説明しちゃうおじさん
自分のまわりに、会社の会議でよく議論をしていると、おもむろに席を立ち、ホワイトボードに向かって、4象限を書いて、「これってこういうことかな?」と整理をし始める先輩がいます。

何でも4象限にプロットして説明すれば、「何か賢く見える」、「法則っぽく見える」からいいという単純なことではないけれど、複雑な物事の規則性などを説明してコンセンサスを取るには有効なことも多いと思います。
■4象限おじさんは物事をどう捉えるのに長けているのか?
4象限おじさんは、「ああでもない」、「こうじゃない?」「それもあるね」という議論の中で、物事を頭の中でどのように整理しているから、最終的に4象限に整理して、理解ができてしまうんでしょうか。
物事を理解する基本的な流れとしては、

というプロセスを踏むことが多いです。多くの思考のフレームワークがこの流れを組んでいることがわかるかと思います。3C分析、AIDMAなどもそうですね。この思考プロセスでは具体的にどんなことをするかをお話していきます。
①分類する
乱雑に広がる物体や観念などがあるのを、ある一部分に目を向けてグループを作っていく作業をします。

ある一部分に目を向ける作業では、抽象化の作業をしていることになります。つまり、その観察しているモノや意識しているコトの対象について、ある一部分以外には(無意識的にやってることも多いですが)意図的に目をつむって捨てる作業、即ち捨象作業を行っています。


同質なもの同士を丸で囲って、違うもの同士の間に線が引けるかってことですね。
例えば、自分の会社の同僚を意識したときに、「性別」に目を向けるて男性/女性で分けたり、「年次」に目を向けて先輩/同期/後輩で分けたり、「専門スキル」に目を向けてデジタルリテラシーが高い人や組織マネジメントが得意な人で分けたりすることができます。
このある一部分に目を向けるとき、どの要素や性質に目を向けて選ぶかの観点が大事になってきます。それは何で決めるべきでしょうか?
結論から言うと、どの要素や性質に目を向けるかは目的から逆算するべきです。しゃべりかけるときに敬語で話すべきかどうかを決めるためには、「年次」に目を向けて、仕事を依頼するには、「専門スキル」に目を向けてグルーピングすることになります。
よく使われる性・年代や業種別などをそのまま利用してグルーピングするのは便利で簡単ですが、その問題解決する目的から、本当に目を向けるべき観点はそれで良いのか、自分に一度問いてみる癖を付けると良いです。上の例で仕事を依頼するなら、専門スキルの観点だけでなく、やる気のありなしや、現在その人が抱えている業務量の多寡なども考慮した方が、より良いスタッフィングができることでしょう。
②関係性を明らかにする
分類したあとには、分けたモノ同士の間にはどのような関係性が存在するのかを考えてみます。その関係性を探るためには、以下の方法があります。
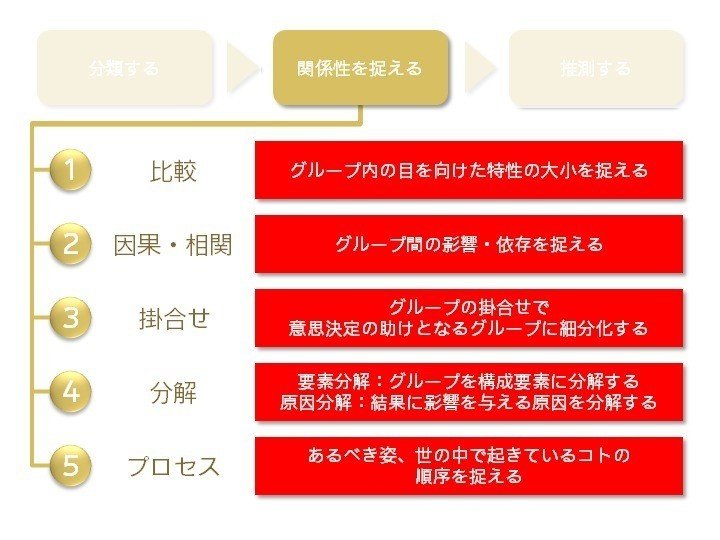
②-1.比較:グループ内の目を向けた特性の大小を捉える
量や質を比較するときは、大きく2つの比較方法に分かれます。時間軸を固定して他者同士で比較して大小を把握するか、同一のモノを時系列で比較して推移を把握するか、です。

比較するには単位・次元を揃える必要があります。数学的な単位だけでなく、概念的なことを比べるときは、①の分類するとき、同じルールでグルーピングされた塊の大きさか、グルーピングの中身はどういう集合になっているかを意識するのが良いでしょう。

図式化するときには、他社同士の比較で全体量が決まってなければ基本棒グラフで、全体量が決まっているなら円グラフやピラミッド図、100%積み立て棒グラフを用いることが多いです。時系列比較であれば横軸に時間を取り、縦にその分量を表す折れ線グラフを用いて変化を把握します。
②-2.因果・相関:グループ間の影響・依存を捉える
グルーピングした集合同士で、一方の動きがもう一方の動きに影響・依存関係がありそうなら、関数になるかもしれないと予想が立てられるかどうかがキーになってきます。

散布図を使ってその法則性を確かめることができます。例え具体的なデータがなくても、Aが極端に大きい場合もう一方のBはどうなるか、Aが極端に小さいときBがどうなるかを考えて4象限で表現してみるとその関係性が見えてくるかもしれません。そうです、これが4象限おじさんの登場です。

物事を捉えたときに、それらの影響関係性に気づき、グラフ化していたのです!②-1の時系列比較の折れ線グラフと違うのは、その関係値を時間での変化を見てるのではなく、単位や次元を合わせたモノの他者同士の関係性を見ているということです。
②-3.掛合せ:グループの掛合せで意思決定の助けとなるグループに細分化する
2グループ間の影響に目を向けて法則性を捉えるのではなく、グループ同士を掛け合わせて新しいグループを作り出します。抽象化するときに目を向けた性質同士を掛け合わせて作り出されるセグメントは、意思決定に役立つ細分化がされなければ意味がありません。
このグループの掛け合わせをする1つに、2×2のマトリクス表にして整理することができます。これは掛け合わせる集合の要素をそれぞれ定量的に比較して、大小✕大小でそれぞれの組み合わせが意味付けされ、意思決定するためのセグメントが行えれば、それは意味のある掛け合わせだったことになります。
有名なフレームワークで言いますと、そのタスクの優先順位を付けるとための振り分けとして、「緊急性×重要性マトリクス」、仕事での人との関わり方を決めるために「WILL×SKILLマトリクス」があったりします。
グループ同士を掛け合わせて、新たなグループを作り出して把握する方法として他にも、ベン図を用いてそれぞれの共通部分である積重合などをつくり、それらのセグメントに価値を見出したり、どこの集合部分を狙っていくのかを捉えるやり方があります。
マトリクス表にするときは、比較する項目(軸)が定量的でそれぞれの大小✕大小で集合を作り出すのに対して、ベン図では、元の比較する集合が量ではなく性質にフォーカスした集合同士であることが異なります。

②-4.分解: 要素分解;グループを構成要素に分解する
原因分解;結果に影響を与える原因を分解する
要素分解は静的で、原因分解は動的であると分けて考えています。

○要素分解
要素分解では、どういう構成要素でできているか中身の要素をMECE的に探すことになります。

例を使ってみます。
利益=(商品・サービスの販売単価 − 原価) ✕ 数量 − 獲得コスト
細ければいい訳ではありません。どの要素に注力すればいいのか、若しくは何を修正していけばいいのかなどの、意思決定の判断材料にできるレベルの粒度にする必要があります。
○原因分解
AからBに働きかけた結果、Bが変化する。この変化が起きた原因を分解します。

例えば、行動に関して、B=matのフレームワークがあります。
B=mat (B=行動、m=モチベーション、a=アビリティ、t=トリガー)
行動を起こすためには、モチベーション(動機)、アビリティ(能力)、トリガー(きっかけ)の3つの要素が揃うことが必要というように、原因分解されています。
要素分解も原因分解どちらも基本四則演算で表すことができます。図式化するときは、足し算で済む場合は樹形図を用いることが多いです。
②-5.プロセス:あるべき姿、世の中で起きているコトの順序を捉える
物事が何か起こるときに、結果までの間にどういう段階が挟まれてその結果が生まれているのかを捉えて、順序に再現性があることに気付けるかです。最初に少し触れたAIDMAやPDCAなどが典型的な例です。
図式化するときは、矢印で結んで行き表現することが多いです。循環する場合は円のように矢印が繋がります。

③推測する
②でそれぞれのグループ同士の関係性を捉えられると、未知の個別な事象が来ても、既知の関係性からそれらの結果が予想できるようになります。
つまり、再現性が期待できることになります。
■寿司のネタとわさびの量の関係
林修先生もこの4象限おじさんの能力をとても身につけられている方だと思っています。初耳学という番組で、「高級寿司店では寿司のネタによってワサビの量が調整されている」ということを解説するために、4象限グラフを取り出し、見事に説明されていて感動しました。
この場合、知りたいこととしては、ワサビと寿司ネタの関係性です。
そもそもなぜワサビを寿司に使うのかということを知らないとこの関係性は明らかにできません。ワサビは魚の生臭さを消すために使用されるようです。
そうなると、元々の臭みの違いや、ワサビの効き方の違いが大事になってきます。ワサビの辛味成分は脂に包み込まれるとその仕事量が減ってしまうそうでして、赤身の魚は白身魚やイカやタコと比較すると、脂の量が多いため、ワサビが効きにくくなるので、予め多めにワサビを入れておくそうです。
これを横軸にそれぞれの魚の脂の量を取り、縦軸にワサビの仕事量として、その関係値によって入れるべきワサビの量をプロットさせていました。
■分析力があるという人とは?
「問いを立てる力」と「ゴールを想像する力」と並んで重要な「分析する力」の基本は、この抽象化、グルーピング、関係性を捉えるというのが基本になると思います。このプロセスと、どのような捉え方を意識しながら身の周りのことを捉えると、乱雑に見えていたものが段々と整理できるようになってくると思います。
分析能力があると言われる人達は、自然とこの①、②のプロセスを踏んで、問題解決のために物事を構造的に捉えて、人に伝達できる人達なんだと思います。
読んでもらった人の何か新しい発見があると嬉しいです。
この記事が気に入ったらサポートをしてみませんか?
