量子力学の基礎のキソ

こんにちは、ヒラタです。今回は僕の好きな物理の話をします。

量子力学と†量子力学†

量子力学は原子や分子といった非常に小さなものについての物理分野です。「波動」とか「不確定原理」とかSFチックな用語が多いので、エセ科学好きの方々には結構ウケが良いらしく、最近は彼らの†量子力学†を本気で信じる人もいるようです。

「思い込みをうまく利用しよう」

量子力学的には思い込みのエネルギーの周波数と同じものが同調して引き寄せるから🙄
思い込みのエネルギーはその思い込みが強力であれば強力それを引き寄せる力が強くなり、現実化していきます
成功者は「自信がある」人が多いですが、その自信には根拠はありません✅

— 高橋宏和＠量子力学コーチ (@ei_infinity) February 15, 2021

３コママンガ

しかし、世の中には真面目に量子力学を学びたい人たちも一定数おり、その層のために教授たちは量子力学の参考書をたくさん作っています。自分も何冊か読んだことがありますが、他分野に比べて初見殺しの本が多い印象があります。

その理由の１つに「図が少ない」ことがあります。図は物事の直観的な理解につながります。学生たちは教授側が思っている以上に図を欲しているのです。字が大きくて図がいっぱいの教科書は最高です（個人の感想）

そこで、今回は量子力学の基礎のキソの話を図マシマシでまとめていきたいと思います。

古典との違い

簡単のため１次元で説明します。
高校から勉強してきた古典の世界では、物体の運動の状態は２つのパラメータで決めることができました。位置と運動量です。

点が状態、曲線が運動（図は単振動ver）

横と縦の座標を決めるだけで、物体の「状態」は完全に決定します。言い換えると、この２つが決まれば他のどの物理量も１つの値に定まります。例えば、おなじみの運動方程式ma=Fは加速度（未来）を定めます。

しかし、原子レベルになると物体の位置と運動量の値が１つに定まりません。先ほどと違って、測るたびに値が乱れてしまいます。各観測値を座標平面にプロットしていきましょう。

たくさんの点が集まって２次元の図形になりました。この図形が物体の「状態」といえます。しかし、この図形上でもたくさんプロットされた点と１回しかプロットされなかった点があるはずです。

そこで、もう１本座標軸を増やして「プロットされた回数」を表示してみます。こうすると、先ほどの２次元図形は３次元的な山に化けます。

これはいわゆる確率分布のグラフで、古典では「点」としていた物体の状態は量子レベルだとこういう「山」として扱うことになります。この山の特徴を見ていきましょう。

山を眺める

まず、この山を上空からのぞいてみます。最初の２次元図形が見えます。

状態に応じてこの図形の形状は様々に変化しますが、面積はほぼ同じ値になります。つまり、横幅が狭い図形なら縦幅は広くなります。

横幅→０とすると縦幅→∞

これは、「無理やり位置の値のゆらぎを少なくすれば運動量のゆらぎ幅が大きくなる」という意味で、いわゆる不確定関係の１種です。

次にこの山を横から見てみましょう。位置と運動量、それぞれの分布が見えるはずです。

この２つの分布グラフは、一方の広がりが小さいと他方の広がりがでかくなるという対応関係があります。先ほど述べた不確定関係というやつです。

この図から気づく人もいるかもしれませんが、実はこの２つのグラフはフーリエ変換で結びついています。

※フーリエ変換とは…
入力したグラフを様々な周波数の波の混ざり合わせと捉え、それらの周波数の分布を出力する変換。

つまり、一方の分布を決まれば、他方の分布も自動で決まるわけです。

山を分解する

物質の「状態」を考える上で、毎回のように３次元の山の絵を書いているのでは面倒です。もっと便利な表記を考えてみましょう。

下準備として、いくつかの山を選んで順番を振って状態列を作っておきます。

そして、目の前の山をこの集合列の要素を組合わせてできたものと捉えます。

こうすると、各項の係数(3,5,1)さえ分かれば、山の形がイメージできます。つまり、物体の状態を係数のベクトルとして表せるということです。

このベクトルは「状態ベクトル」や「ケットベクトル」と呼ばれ、実際めちゃくちゃ便利なのですが、実は状態列を作る段階で問題が生じます。

１．全パターンの状態をそれらの組み合わせで表せるか（完全性）
２．組み合わせの表記は一意なのか（線形独立性）

線形代数経験者なら分かると思いますが、線形独立かつ完全なベクトル列は使い勝手が良い反面、作るのが大変です。

また、ただ山を分解するだけでなく、ベクトルとして計算できるようにしたいので、基底の状態ベクトル同士の内積は０である必要があります。（直交性）

さらに、下のような２つの状態ベクトルは本質的に等価なので、状態ベクトルの大きさは一定に揃えるというルールが必要になります。

これは表記の一意性に関わる話で、「山を作るときに点をプロットする回数を一定にする」ことと対応します。（規格化）

山は波の集まり

上で挙げた条件を全部満たすような状態列はそういくつもありません。パッと思いつくものだとフーリエ列とデルタ列くらいです。

とりま脳死でx分布の山をデルタ列分解しましょう。

状態ベクトルは無限次元

分解した各状態成分はx側から見るとただの縦棒ですが、p側から見ると下のように波打って見えます。

デルタ関数と三角関数がフーリエ変換で結ばれてることを知ってる人にとっては、この結果は当たり前かもしれません。でも、状態をx方向にデルタ列という「正規完全直交列」で分解したらp方向でもフーリエ列という「正規完全直交列」で分解されるのはちょっと面白いですね。

フーリエ変換で正規完全直交性は失われない

このx方向のデルタ列集合（p方向でのフーリエ列集合）に属する状態たちは、いずれも「位置が100%確定している」という点で共通しています。これらの状態は特に位置固有状態と呼ばれます。

上の分解操作をp方向でのデルタ列集合（x方向でのフーリエ列集合）について行うこともできます。

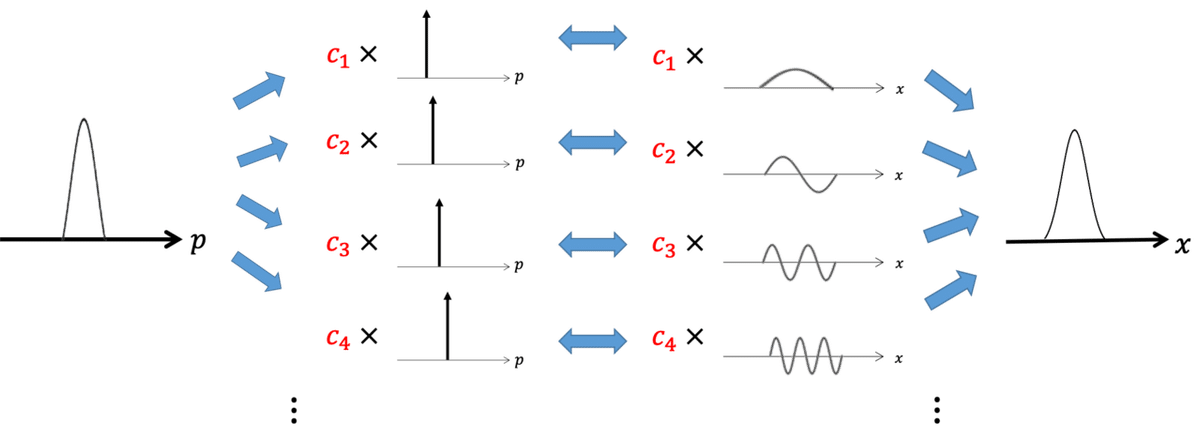
運動量が100%確定している状態での分解

この分解に用いた状態たちは運動量固有状態と呼ばれます。キャンパス内を歩いてると、「位置固有状態＝デルタ関数！」「運動量固有状態＝三角関数！」と叫んでる人を見かけますが、それは状態の山をx方向から覗いた場合に限ります。p方向から見るとその対応はちょうど逆転するはずです。

これらの固有状態を基底にすることで、状態ベクトルがちゃんと定義できます。頼もしいやつらです。

おわりに

上で話したことは初歩的な量子力学の内容ですが、こういった視覚的な説明はあまり見られないのでトライしてみました。

量子力学を学んでも心の振動数が上がることはありませんし、アニメ・ラノベなどで主人公たちが「量子テレポーテーション！」と叫んで瞬間移動するシーンでは少し萎えるようになります。実生活で役立つことなんてほぼゼロです。

それでもいつかこの学びが活きる日がくると信じて、今日もシュレーディンガー方程式を解きましょう。。。