行列が見えるようになった話

こんにちは、ヒラタです。今回はちょっと数学の話をします。

大学数学は面白いのか

私は高校の頃、数学の問題を解くのが好きでした。自分でオリジナルの問題を作っては友達に解かせていたものです。

関数、幾何、確率、整数、数列...

いろいろな分野があるのも魅力ですが、私にとっての高校数学の面白さは「問題の視覚化」ができることにありました。

関数の問題では座標平面にグラフを書いたり、確率の問題では状況をイラストにしたりして、そういったイメージが数式とつながる瞬間が最高に面白いのです。当時の私にとって数学は「書く」というより「視る」ものでした。

しかし、大学に入った途端、私は数学の世界が視えなくなりました。アイツが私の前に姿を現したのです...

こいつきらい

ベクトルは矢印に見えるが、行列はただの数の羅列でしかない。そう感じてしまった当時の私にとって線形代数の勉強はちっとも楽しくありませんでした。

簡約化したり、行列式求めたり、対角化したり…。一応答えは出せるし単位も来ます。しかし、どうしてもこの教科が好きになれませんでした。

それから約半年後、線形代数の参考書を何気なく開いたとき、どういうわけか私は「行列の見方」が分かった気がしました。そして、その見方をすれば、参考書に載ってる定理も当たり前のことだと気づきました。

線形代数の講義がとっくに終わった私にとっては遅すぎる気付きでしたが、世の中には私と同じくこの行列とかいうヤツに人生をめちゃくちゃにされた方も少なからずいると思うので、ここにその倒し方を記しておくことにします。

行列をイメージする

最初に断っておくと、行列の見方はベクトルのときのように１つではないと思います。私が持ってるイメージは大きく分けて３つあります。まずは１つ目、、、

その１：座標系の変換

行列とベクトルをかけるとベクトルになります。このとき、入力したベクトルと出力されるベクトルの間にはどんな関係があるのでしょうか。実際に調べてみましょう。簡単のため２次元で。

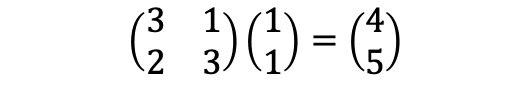
ベクトル( 1 , 1 )がベクトル( 4 , 5 )になりました。この意味は下のように変形すると視えやすいです。

つまり、上式の意味は「( 3 , 2 )と( 1 , 3 )を基底とする斜交座標系で( 1 , 1 )と表される点の座標はxy平面では( 4 , 5 )と表される」だったわけです。それぞれの行列は独自の斜交座標系を持っていて、ベクトルとかけるとxy平面座標との対応が視えるわけです。行列をかけることは座標系を歪めて基底を変換する行為であると言えるでしょう。

この見方は図に書ける良さがありますが、3次元までしかイメージできないのが難点です。関数の変数変換を可視化するのに便利です。

例えば、xy平面における双曲線x^2-y^2=1はX=(1/2,-1/2)とY=(1/2,1/2)を基底とすれば反比例のグラフY=1/Xに見えます。座標系を変えれば、グラフの見方も変わるわけです。

その２：列ベクトルを並べたもの

その１の多次元ver.です。行列のサイズによらず、行列の中には座標系が存在します。これは特に「像空間」と呼ばれます。

上図のように、列ベクトルが張る空間（像空間）をイメージするとこの空間の次元は「線形独立な列ベクトルの最大個数」です。この数はrankと呼ばれます。この列ベクトルたちに基本線形操作を施すと、空間が歪みますが次元が減ることはありません。

※基本線形操作とは…
(i)ベクトルをスカラー倍する（０倍は✗）
(ii)あるベクトルに他のベクトルを加える
(iii)ベクトルの並び順を入れ替える

だから、行簡約化（基本線形操作の組み合わせ）をしてもrankは変わらないわけです。簡約化行列の形をイメージすれば、「線形独立な列ベクトルの最大個数」と「線形独立な行ベクトルの最大個数」は必ず同じ値になります。

青で囲まれた数字の数＝rank

このことは行列を転置してもrankの値が変わらないことと深く関係しています。

その３：ベクトル操作

こういうのじゃない

行列とベクトルをかけるとベクトルになります。この過程を「入力したベクトルの各成分に行列が何らかの操作を加えて別のベクトルに変えてしまう」と捉えます。

「操作」は一度してしまったら取り返しのつかないタイプと後で別の操作を加えれば元の状態に戻せるタイプの２種類があります。後者のタイプを正則行列といいます。

例えば、どんなベクトルもゼロベクトルに変えてしまう行列は正則ではありません。また、列ベクトルに平行（１次従属）なものがある行列もダメです。

斜「交」座標系にならない

上図のように行列の基底が平行だと、 xy平面座標の中に対応相手がいない点が生まれます。これにより、像空間の次元が入力したベクトルの次元より小さくなります。

つまり、正則でない行列を掛けられたベクトルは情報(自由度)を失うわけです。この失う情報の量は行列のrankによって決まります。

正則行列をかけても、ベクトル（行列）の情報量が変わらないのは正則行列が基本線形操作の組み合わせだからです。

※基本線形操作とは…
(i)ベクトルをスカラー倍する（０倍は✗）
(ii)あるベクトルに他のベクトルを加える
(iii)ベクトルの並び順を入れ替える

正則行列は相手の情報量を減らさない、この事実は正則行列を左右からかけられても、行列のrankの値は変わらないことに深く関係しています。

また、行列の正則性はその行列のdet（列ベクトルによってできる平行多面体の体積）を調べることで分かります。正則行列はどの列ベクトルも一次独立なので、行列式（体積）は正になります。しかし、一次従属が入っていると０になります。

こうして、行列のrankとdetが正則性という一本の線でつなげられました。ここから、実はrankを「det>0の小行列のサイズの最大値」と解釈することもできます。これの直観的なイメージはrankを測るときにベクトルの順番を入れ替えても大丈夫！と気づけば掴みやすいです。

小行列のサイズ=rank

話をまとめると、「行列は座標系（像空間）と捉えられる一方、操作（線形写像）として捉えることも可能」というのが私の結論です。この解釈は一見全く異なるようですが、rankやdet等の概念で密接につながっているわけです。

おわりに

上で話したことはちゃんとした教員に線形代数を教われば自然と身につくはずの内容ですが、こういった視覚的な説明はあまり見られないのでまとめてみました。

線形代数に限らず、直観的なイメージの話は世の参考書や大学講義でもっと取り上げてくれてもいいんじゃないかと思ってます。結局、記憶に残るのって数式よりイメージな気がするので。

ずいぶん長くなってしまいましたが、この辺りで筆を置くことにします。皆さんの行列へのイメージが少しでも良いものになりますように、、、