
時系列データをpython【#2】相互相関
時系列データを分析とか予測をしたことがなかったのでやっていきます。「株価をpython」というブログの続きです。
以下の流れで進めていこうと思います。
今回は、「2.サンプルデータの自己相関・相互相関」のあたりを進めていきます。
1.サンプルデータの作成
2.サンプルデータの自己相関・相互相関
3.サンプルデータのDTW
4.オープンデータの追加
5.データの予測
#1でサンプルデータを作ったので、それらの相互相関を見ていきます。事前情報として、pythonのstatsmodelsのccfで計算できることを教えてもらっていました。ただ、statsmodelsのccfの挙動を理解していないので、ccfの理解からしていきます。
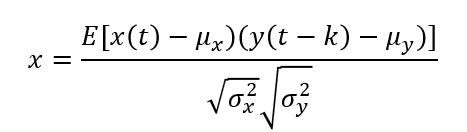
上記数式はインターネットから拾ってきました。時系列データx,yだと思います。tはある時点の時間だと思います。サンプリングが1日単位だったら、t=1日、2日、3日…みたいな。kはずらす時間のようです。tと同じ単位で、k=1日だったら、1日ずらすという意味のようです。μは平均、σは標準偏差です。Eは期待値なので、サンプル数で最後に割ればいいようです。(数式は苦手、、、)
ここで、tが1から4(xもyもサンプル数が4つ)までしかないとしましょう。そうすると、kをずらすなら0から3までしかずらせません。ここで気づくのがずらしていくと、E[x(t) * y(t)]のペアが4つ、3つ、2つ、1つと減っていくことです(↓のところの”ない”は計算できない)。

ということは、サンプルがいっぱいあった場合、少しずらしてサンプル数が減ってもそれなりにいい感じの値はでそうですが、ラグが最後までとき、1個のx,yのペアで算出した相互相関係数って確からしいのかな?って思いました。なので、サンプル数が十分に残る程度のラグに限定したほうがよさげかなぁと思いました。あと、分母のσと分子のμはサンプルのペアが減っていく中でも、ペアが最大のとき(=サンプル数)の時のσとμを使っている点にご注意。サンプルのペア数が減ってもσもμも再計算しないってこと。手計算のときにいろいろしくって、気づきました。


excelで手計算したのが↓です。F列の橙色のセルがstatsmodelsのccfを使った答え。15行目にずらす量をk=で記載していて、その下にxとyの計算ペアを書いていき、29行目に最終的なk=nのずらし量ごとの相互相関係数を記載しています。計算ペアの例として、H列のk=4に緑を塗っています。同じいろのC列とB列のペアで分子を計算しています。k=9は分子の計算ペアが1つしかありません、、、これはたしからしいのでしょうか。使わないほうが無難?

このあと、xを昇順に並べて同じことをしてみました。するとへんてこなことに相互相関係数が-1を超えています。いいのでしょうか。。。分子の計算ペアが少なすぎて、おかしなことになってそうです。この場合、xを昇順しているので、そこらへんが相互相関と相性が悪そうです。なので、ラグの設定はサンプル数が一定以上ある範囲におさめたほうがよさそうです。

もう少し考えてみます。標準偏差ってsqrt(E[x-u]^2)なので、Expectationが入っています。これって期待値を取る(=平均みたいに、最後にサンプル数で割る)ので、大きい値と小さい値をならすことになります。そのならした値が分母に来ていて、ラグが大きくなる→ペア数が少なくなるという状態でそのデータが極端に大きい、小さい値の場合、分子が分母より大きくなる可能性はありそうです。
ということで、手計算してみて、statsmodelsのccfはラグを設定した状態で使うのがよさそうということがわかりました。では次は、実際のデータで試してみようと思います。
※ChatGPT3.5を使いながらコードは書いています。環境はgoogle colabです。
この記事が気に入ったらサポートをしてみませんか?
