
数学に悩む高1へ
こんにちは。たまごです。
今回は、多くの人が悩むであろう数学について話していこうと思います。ただ「問題を解こう」という、いわば薄っぺらい内容ではなく、具体的な方法を解説出来たらなと思います。
まだ高ーなので、一年内容を中心に話します。
なお、今回はかなり長くなっているので、”3.数学の勉強法” だけでも見てくださると今後に生かせるではないかと思います。
1.今の現状を知る
ただ数学がわからない・苦手だといっても、数学の世界は非常に広いので、まずは自分はどの分野の数学が苦手か、を考える必要があると思います。
主に高校数学は4つの分野(代数・関数・幾何・確率統計)に分かれています。
<代数>
この分野は、主に式と証明、集合と論証、複素数などを扱います。
高校一年生ならば、展開・因数分解、方程式・不等式、集合と命題、整数などが当てはまります。
<関数>
この分野は、二次関数や三次関数、指数関数や微分積分などを扱います。
一年生は二次関数のグラフ、最大最小、判別式、二次不等式などが当てはまります。
(判別式や二次不等式などは代数にも絡みます)
<幾何>
この分野は、三角比・三角関数、図形の性質、複素数平面などを扱います。
一年生は三角比、円周角や内心外心、などが当てはまります。
(三角関数は関数、複素数平面は代数、数IIでやる図形と方程式は代数、関数にも絡みます)
<確率統計>
この分野は、場合の数と確率、データの分析、統計的な推測などを扱います。
一年生は場合の数と確率、データの分析が当てはまります。
(代数分野の集合は、確率と非常に密接です)
以上4つにたいていは分類されます。必ずしも単元と分野が一対一対応するわけではないですが、自分は何の分野が苦手なのかが掴めるとgoodです。
2.単元ごとの解説(分野別に)
代数
この分野は数学の基盤となる、ある意味最重要分野だと思っています。だからこそ、なんとなくではなく完璧に身に着けてほしいです。
<展開と因数分解>
まず、$${(ax+b)(cx+d)=acx^2+(ad+bc)x+bd}$$の公式を当たり前に使えるようにしましょう。これが因数分解のたすき掛けにつながります。
また、応用範囲の展開と因数分解は、1つの文字に注目することでほぼ解けると思います。
例えば、$${abc+ab+bc+ca+a+b+c+1}$$を因数分解することを考えると、
$$
\begin{array}{} 与式 &=& (bc+b+c+1)a+bc+b+c+1 \\\ &=& (a+1)(bc+b+c+1) \\\ &=& (a+1)((c+1)b+c+1) \\\ &=& (a+1)(b+1)(c+1)\end{array}
$$
となります。
1段目で$${a}$$に着目、2段目で$${b}$$に着目したが、a,b,cどの文字も次数が同じなのでどの文字で着目しても因数分解可能です。
<一次不等式>
まずは不等式$${A>B}$$が成り立つとき、以下の4つが成り立つことを理解しましょう。
$${A+C>B+C}$$
$${A-C>B-C}$$
$${AC>BC,\frac{A}{C}>\frac{B}{C}}$$ $${(C>0)}$$
$${AC < BC,\frac{A}{C}<\frac{B}{C}}$$ $${(C<0)}$$
これがわかれば、与えられた不等式を$${x<(or>)}$$の形にし、数直線上に表すことで基本的な問題はほぼ完璧です。(図1)
あとは、定数$${a}$$や$${\sqrt{}}$$が入った不等式などでは、大小関係に気を付けて数直線上に表すトレーニングをしましょう。
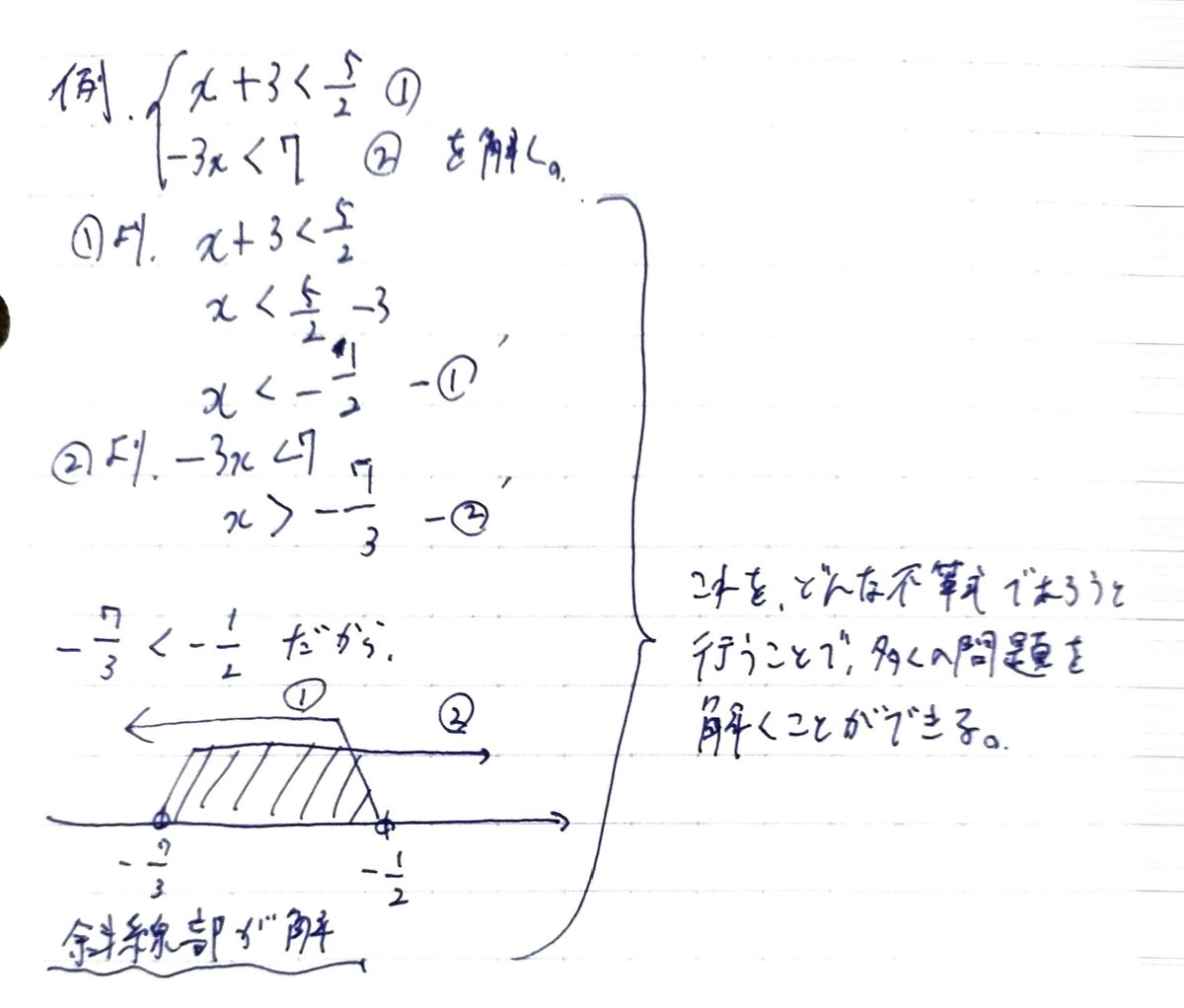
<集合と命題>
とにかくベン図を描きましょう。集合で出てくるド・モルガンの法則や、命題の逆・裏・対偶、必要十分条件も慣れないうちはベン図から視覚的に理解することが出来ます。
また、場合の数と確率では集合の要素の数え上げを行います。そのときに、
$${n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A \cap B)-n(B \cap C)-n(C \cap A)+n(A \cap B \cap C)}$$ という公式も出てきますが、これを初めから丸暗記したところで何の力にもなりません。
そこでベン図の登場です。実際、三つの集合のベン図(図2)を書いて証明してみることで、その公式を自分のものにすることができます。
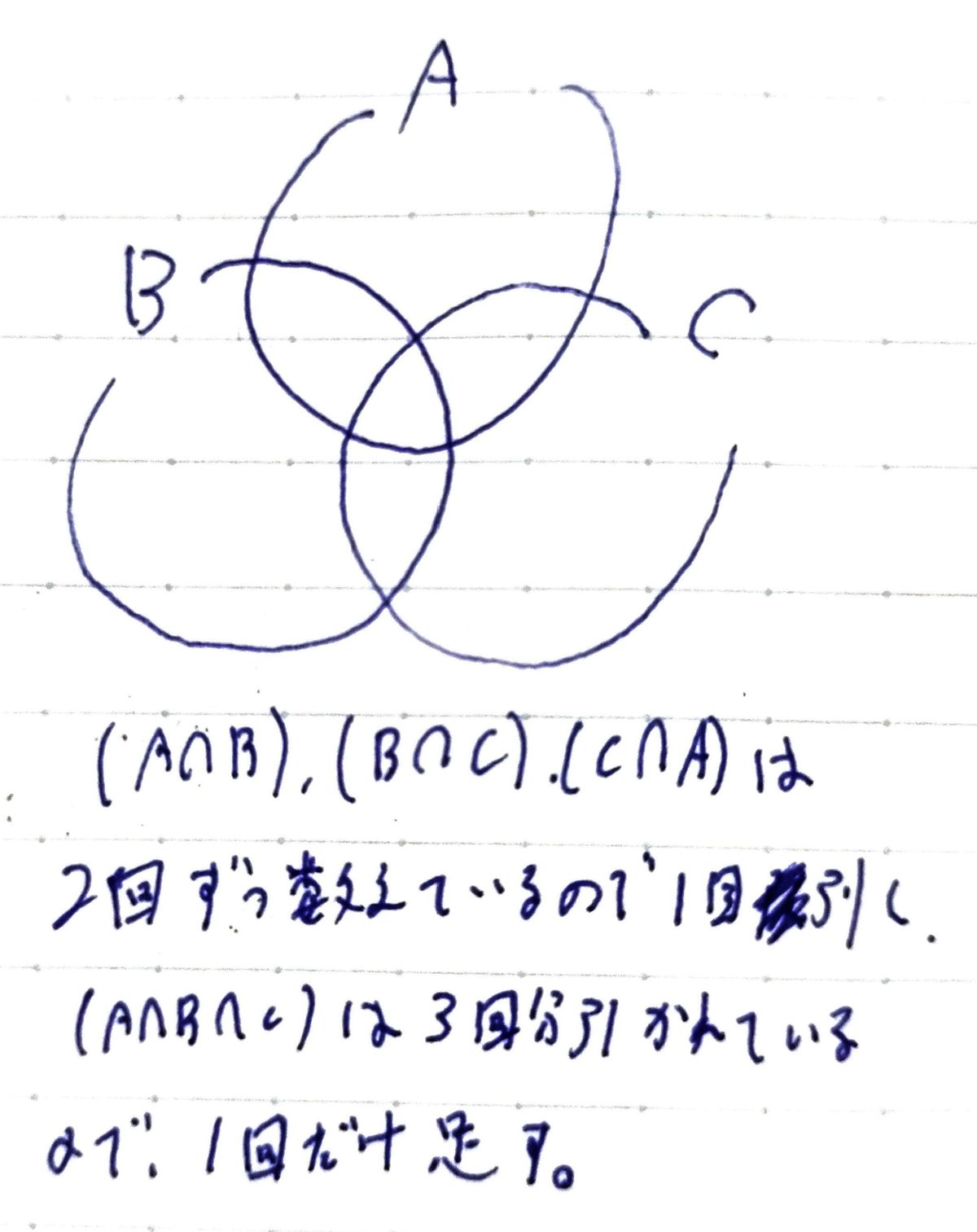
ちなみに証明の際には、すべて足して重なりを引くことをしますが、これは場合の数・確率でも非常によく使うものです。
<整数>
整数は非常に範囲が広いので、余りで絞り込む・不等式で絞り込むの二つについて話します。
ー余りで絞り込むー
例えばこんな問題。
$${n^2+n}$$は2の倍数であることを示せ。($${n}$$は整数)
この場合、すべての整数においてこれが成り立つことを示したいので、2の倍数であるより、$${n}$$を2で割った余りで場合分けをします。
解答
$${N=n^2+n}$$とおく。$${n}$$を2で割った余りで場合分けをすると、
$${n=2k または n=2k+1 (kは整数)}$$ となる。
(i)$${n=2k}$$ のとき、
$${N=(2k)^2+2k=4k^2+2k=2(2k^2+k)}$$
$${2k^2+k}$$ は整数だから、$${N}$$は2の倍数。
(ii)$${n=2k+1}$$ のとき、
$${N=(2k+1)^2+(2k+1)=4k^2+6k+2=2(2k^2+3k+1)}$$
$${2k^2+3k+1}$$ は整数だから、$${N}$$は2の倍数。
以上より、全ての整数で$${N}$$は2の倍数である。
このように余りに着目することで、全ての整数に当てはまることを証明することができます。
ー不等式で絞り込むー
例えばこんな問題。
自然数$${a,b,c}$$で、
$${\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1}$$ $${(a \leqq b \leqq c)}$$
も満たすものを全て求めよ。
この場合、$${a,b,c}$$ があまりにも大きいと
$${\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}$$は1に届かなくなります。だから、不等式をうまく使って範囲を絞り込み、場合分けをします。
解答
$${a>3}$$ のとき、$${3< a \leqq b \leqq c}$$となるから、$${\frac{1}{c} \leqq \frac{1}{b} \leqq \frac{1}{a}<\frac{1}{3}}$$。
このとき、
$${\frac{1}{a}+\frac{1}{b}+\frac{1}{c}<\frac{1}{3}*3=1}$$ より、$${a>3}$$は不適。よって$${a \leqq 3}$$
$${a}$$は自然数だから、$${a=1,2,3}$$
(i)$${a=1}$$のとき
$${\frac{1}{1}+\frac{1}{b}+\frac{1}{c}=1}$$
これを満たす自然数$${b,c}$$は存在しない。
(ii)$${a=2}$$のとき
$${\frac{1}{2}+\frac{1}{b}+\frac{1}{c}=1}$$ $${\frac{1}{b}+\frac{1}{c}=\frac{1}{2}}$$
$${b>4}$$のとき、$${4< b \leqq c}$$ より $${\frac{1}{c} \leqq \frac{1}{b}<\frac{1}{4}}$$
このとき、$${\frac{1}{b}+\frac{1}{c}<\frac{1}{4}*2=\frac{1}{2}}$$となるため不適。
よって$${a \leqq b \leqq 4}$$ となるため、$${b=2,3,4}$$
$${b=2}$$ のとき、$${\frac{1}{2}+\frac{1}{c}=\frac{1}{2}}$$
$${c}$$は存在しない
$${b=3}$$ のとき、$${\frac{1}{3}+\frac{1}{c}=\frac{1}{2}}$$
$${c=6}$$
$${b=4}$$ のとき、$${\frac{1}{4}+\frac{1}{c}=\frac{1}{2}}$$
$${c=4}$$
したがって、$${(a,b,c)=(2,3,6),(2,4,4)}$$
(iii)$${a=3}$$のとき、
$${\frac{1}{3}+\frac{1}{b}+\frac{1}{c}=1}$$ $${\frac{1}{b}+\frac{1}{c}=\frac{2}{3}}$$
$${b>3}$$のとき、$${3< b \leqq c}$$ より $${\frac{1}{c} \leqq \frac{1}{b}<\frac{1}{3}}$$
このとき、$${\frac{1}{b}+\frac{1}{c}<\frac{1}{3}*2=\frac{2}{3}}$$となるため不適。
よって$${a \leqq b \leqq 3}$$ となるため、$${b=3}$$
このとき、$${\frac{1}{c}=\frac{2}{3}-\frac{1}{3}=\frac{1}{3}}$$ $${c=3}$$
以上より、$${(a,b,c)=(3,3,3)}$$
(i)~(iii)より、$${(a,b,c)=(2,3,6),(2,4,4),(3,3,3)}$$
これはかなり複雑ですが、やっていることは一つの文字の上限を考えることで、場合分けの量を少なくしています。
このように、不等式を用いることである定数や式の値を絞ることを不等式評価といいます。
関数
そもそも関数の定義を理解していない人もいるのではないでしょうか?
関数とは、ある値に対してもう一方の値がただ一つに定まる対応の事を指します。決してグラフとイコールではありません。(関数を視覚化したものがグラフです。)
今回は、グラフの最大最小と二次方程式・二次不等式について話します。
<グラフの最大最小>
まず、グラフに値の増え方は単調であるかそうでないかに分けられます。
単調とは、変数の値が増えるほどもう一方の値も増え続ける(逆も然り)変化の仕方のことをいいます。
もし単調なグラフ(図3)ならば、最大最小は必ず変域の端で現れます。
しかし、単調でないグラフ(図4)であると、変域の途中で最大または最小をとる場合もあります。これが2次関数の最大最小を厄介にしている正体です。


では、単調でないグラフ(今回は二次関数)の最大最小の求め方を今一度確認しましょう。
例えば、$${y=x^2-2x+2 (-1 \leqq x \leqq 2)}$$のグラフは↓のようになるので、

$${Max: 5 (x=-1)}$$ $${Min: 1 (x=1)}$$となります。
$$
\begin{array}{} y &=& x^2-2x+2 \\\ &=& (x-1)^2+1\end{array}
$$
となるため、$${x=1}$$がこの放物線の軸です。
この時、最大値は軸からより離れている端で取り、最小値は軸が変域内にあるので軸で取っています。(これが後の場合分けにおいて必要なとらえ方です。)
次に、$${y=-x^2+2x+2 (-1 \leqq x \leqq 2)}$$のグラフは↓のようになるので

$${Max:3 (x=1) Min:-1 (x=-1)}$$となります。
$$
\begin{array}{} y &=& -x^2+2x+2 \\\ &=& -(x-1)^2+3\end{array}
$$
となるため、$${x=1}$$がこの放物線の軸です。
この時、最大値は軸が変域内にあるので軸で取り、最小値は軸からより離れている端で取ります。(これも場合分けに必要)
以上を踏まえて、文字定数の場合分けについて話します。
二次関数において、場合分けは以下のとおりです。
(i) 下に凸のグラフのとき
最大値は軸から離れている方の、変域の端で取る
→軸と変域の中央の位置関係で場合分け
最小値は軸で取る
→軸と変域の両端の位置関係で場合分け
(ii)上に凸のグラフの時
最大値は軸で取る
→軸と変域の両端の位置関係で場合分け
最小値は軸から離れている方の、変域の端で取る
→軸と変域の中央の位置関係で場合分け
例1. $${y=x^2-2ax+1 (-1\leqq x\leqq1)}$$の最大最小
$$
\begin{array}{} y &=& x^2-2ax+1 \\\ &=& (x-a)^2-a^2+1\end{array}
$$
となるため、軸は$${x=a}$$となる。
最大値は、軸と変域の中央の位置関係で場合分けする。
変域の中央は、$${\frac{-1+1}{2}=0}$$である。
(i)$${a<0}$$のとき、$${Max:-2a+2 (x=1)}$$
(ii)$${a \geqq 0}$$のとき、$${Max:2a+2 (x=-1)}$$
$${\therefore Max={-2a+2(a<0),2a+2(a \geqq 0)}}$$

最小値は、軸と変域の両端の位置関係で場合分けする。
(i)$${a<-1}$$のとき、$${Min:2a+2 (x=-1)}$$
(ii)$${-1\leqq a\leqq 1}$$のとき、$${Min:-a^2+1 (x=a)}$$
(iii)$${a>1}$$のとき、$${Min:-2a+2 (x=1)}$$
$${\therefore Min={2a+2(a<-1),-a^2+1(-1\leqq a\leqq 1),-2a+2(a>1)}}$$

例2. $${y=-x^2+2x+2 (a\leqq x\leqq a+2)}$$の最大最小
$$
\begin{array}{} y &=& -x^2+2x+2 \\\ &=& -(x-1)^2+3\end{array}
$$
となるため、軸は$${x=1}$$となる。
最大値は、軸と変域の両端の位置関係で場合分けする。
(i)$${a>1}$$のとき、$${Max:-a^2+2a+2 (x=a)}$$
(ii)$${a\leqq 1\leqq a+2 \therefore -1\leqq a\leqq 1}$$のとき、
$${Max:3 (x=1)}$$
(iii)$${a+2<1 \therefore a<-1}$$のとき、$${Max:-a^2-2a+2 (x=a+2)}$$
$${\therefore Max=-a^2+2a+2(a>1),3(-1\leqq a\leqq 1),-a^2-2a+2(a<-1)}$$

最小値は、軸と変域の中央の位置関係で場合分けする。
変域の中央は、$${\frac{a+(a+2)}{2}=a+1}$$である。
(i)$${a+1\leqq 1 \therefore a\leqq 0}$$のとき、$${Min:-a^2+2a+2 (x=a)}$$
(ii)$${1< a+1 \therefore a> 0}$$のとき、$${Min:-a^2-2a+2 (x=a+2)}$$
$${\therefore Min=-a^2+2a+2(a\leqq 0),-a^2-2a+2(a>0)}$$

軸が文字のとき、範囲が文字の時によって少し性格は違いますが、やることは基本同じです。難しく考えすぎないようにしましょう。
<二次方程式・二次不等式>
二次方程式$${ax^2+bx+c=0}$$において、
$${x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}}$$となる。このとき、解の個数について考えると、$${\pm}$$があるので解の個数は$${\sqrt{b^2-4ac}}$$によって定まります。つまり、$${\sqrt{b^2-4ac}}$$の$${b^2-4ac}$$に着目すればよい、ということになります。
この$${b^2-4ac}$$を二次方程式の判別式$${D}$$とすると
$${D>0}$$のとき、$${\sqrt{b^2-4ac}>0}$$だから解は2個
$${D=0}$$のとき、$${\sqrt{b^2-4ac}=0}$$だから解は1個
$${D<0}$$のとき、$${\sqrt{b^2-4ac}}$$より、解は0個(複素数まで話を広げると解は2個)
次に、二次関数$${y=ax^2+bx+c}$$と二次方程式の関係について考えます。
この時、放物線とx軸の共有点のx座標は、
$${y=0*x}$$ (関数の定義よりこの書き方にしています。)
$${y=ax^2+bx+c}$$
の共通解だから、代入して
$${ax^2+bx+c=0*x}$$
$${\therefore x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}}$$
よって、放物線とx軸の共有点の座標は
$${(x,y)= (\frac{-b+ \sqrt{b^2-4ac}}{2a},0),(\frac{-b- \sqrt{b^2-4ac}}{2a},0)}$$
つまり、放物線とx軸の共有点のx座標を求めることは、二次方程式の解を求めることに等しい、ということになります。
(一般的に、$${y=f(x)}$$のグラフとx軸の共有点のx座標は$${f(x)=0}$$の解に等しい。)
今、二次方程式と二次関数を結びつけることで、一次元的な解釈をしていた二次方程式を二次元的な視点から見ることができるようになった
、、、といわれてもwhat??となるかもしれないが、二次元すなわち平面的に考えることで、このような問題を考えることができます。
例:$${x^2+3x+2>0}$$となる$${x}$$を求めよ
もし、一次元すなわち数直線的に考えることしかできなかったら、この問題を解くのは困難。しかし、ここで$${y=x^2+3x+2}$$のグラフを考えると、
$${y=x^2+3x+2=(x+1)(x+2)}$$だから、x軸との共有点の座標が$${(x,y)=(-2,0),(-1,0)}$$となるグラフである。
$${y=x^2+3x+2}$$だから、
$${x^2+3x+2>0}$$と$${y>0}$$は同じことを指している。
グラフのy座標$${>0}$$となる$${x}$$の範囲は、グラフより
$${x<-2 ,-1< x}$$とわかる。

この解法は、まさに二次関数をうまく活用した方法です。
では、この上で次のような問題を考えます。
$${-x^2-kx-1<0}$$となる$${x}$$がすべての実数となるとき、実数$${k}$$を求めよ。
これも二次関数を用いて考えます。
$${y=-x^2-kx-1}$$とおくと、このグラフがx軸の下にあればいい。

つまり共有点が0個の時に条件を満たすので、判別式$${D}$$より
$${D=(-k)^2-4(-1)(-1)=k^2-4<0}$$となればよいから、
$${-2 < k < 2}$$
全ての実数$${x}$$において$${x}$$の二次式がとる値が0より大きいか小さいか、という問題は、二次関数のグラフの問題に捉えると解くことができることも多いです。
このように、二次関数は二次方程式・二次不等式と密接にかかわりあっています。ここに限った話ではないですが、別視点からアプローチするというのは数学においても大切なことなので、日頃から意識してみてください。
幾何
幾何では三角比、図形の性質を扱いますが、今回は三角比について話します。(図形の性質は中学の復習内容も多いのと、三角比が高校で初登場なので、スペース的に図形の性質は割愛します。)
<三角比とは>
名前のとおり三角形の比のこと、もっというと三角形の辺の比のことを指す言葉で、三角形の辺が3つあるのでそれぞれ名前がついています。

上図において、$${\theta}$$におけるそれぞれの三角比($${sin,cos,tan}$$)は次のように定義されています。
$${sin\theta = \frac{q}{r}}$$
$${cos\theta = \frac{p}{r}}$$
$${tan\theta = \frac{q}{p}}$$
これは実際に問題を解いて身に着けていきましょう。
例:次の直角三角形の$${sin\theta,cos\theta,tan\theta}$$の値を求めよ。

まず、三平方の定理より$${AB}$$の長さを求めます。
$${AB^2=BC^2+AC^2=3^2+4^2=25}$$
$${\therefore AB=5}$$
三辺の長さがわかったので、三角比を求めていきます。
$${sin\theta = \frac{AC}{AB}=\frac{4}{5}}$$
$${cos\theta = \frac{BC}{AB}=\frac{3}{5}}$$
$${tan\theta = \frac{AC}{BC}=\frac{4}{3}}$$
やっていることは何も難しくないと思います。
<三角比の拡張>
今までは、$${0°< \theta < 90°}$$の場合のみ話してきましたが、角度$${\theta}$$がどんな値であれ三角比を使えるようにする、最強の道具があります。それは単位円と呼ばれるものです。
単位円とは
単純に言うと、半径が1の円の事を指します。一体それがどう三角比と結びつくか、話していきます。
この単位円を座標平面上に図示すると、下図のようになります。

このとき、点Bの座標を考えます。
$${sin\theta =\frac{BP}{AB}}$$であるから、
$${BP=ABsin\theta =sin\theta}$$
これと同様に行い、
$${AP=cos\theta}$$となるから、座標は
$${(cos\theta,sin\theta)}$$となります。
つまり、半径1の円周上の点の座標が、$${sin\theta,cos\theta}$$の値となります。
また、$${tan\theta=\frac{BP}{AP}}$$であるから、$${tan\theta}$$の値は半径$${AB}$$の傾きに等しい。
このように、単位円を用いることで、$${\theta}$$の値が何であっても(負でもいい)三角比の値を求めることができます。
<三角比と角度の関係>
次に、単位円を用いて三角比同士の関係や、三角比の値における角度同士の関係について解説します。
先ほどの図で三平方の定理を用いると
$${AP^2+BP^2=AB^2}$$が得られ、$${AP=cos\theta,BP=sin\theta,AB=1}$$を代入すると、
$${sin^2\theta + con^2\theta =1}$$、、①が成り立つ。
また、$${tan\theta=\frac{BP}{AP}}$$であるから、値を代入して
$${tan\theta=\frac{sin\theta}{cos\theta}}$$、、②が成り立つ。
また、①②から$${sin\theta}$$を消去して、
$${tan^2\theta+1=\frac{1}{cos^2\theta}}$$が成り立つ。
(途中式)
$${tan\theta=\frac{sin\theta}{cos\theta}}$$より、
$$
\begin{array}{} tan^2\theta &=& \frac{sin^2\theta}{cos^2\theta} \\\ &=& \frac{1-cos^2\theta}{cos^2\theta} \\\ &=& \frac{1}{cos^2\theta} &-& 1\end{array}
$$
$${\therefore tan^2\theta+1=\frac{1}{cos^2\theta}}$$
この相互関係の式を使うと、$${sin,cos,tan}$$のどれか一つの値が分かれば、他2つの値も求めることができます。
例:$${sin\theta=\frac{\sqrt{3}}{2}}$$のとき、$${con\theta,tan\theta}$$の値を求めよ。$${(0 < \theta <90)}$$
相互関係の式より、
$${sin^2\theta+cos^2\theta=(\frac{\sqrt{3}}{2})^2+cos^2\theta=1}$$
$${cos^2\theta=1-(\frac{\sqrt{3}}{2})^2=\frac{1}{4}}$$
$${\therefore cos\theta=\frac{1}{2}}$$
また、
$${tan\theta=\frac{sin\theta}{cos\theta}=\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}}$$
$${\therefore tan\theta=\sqrt{3}}$$
(補足)
この問題において、$${cos\theta,tan\theta}$$は必ず正の値をとります。$${(0 < \theta <90)}$$なので、単位円を考えると

この範囲であれば$${cos\theta}$$の値(=点Bの$${x}$$座標)は必ず正となります。
また、$${tan\theta}$$の値(=ABの傾き)も必ず正となります。
次に、角度の関係について調べます。
教科書などにはいろいろ書かれていますが、結局単位円描いたらすべてわかります。なので単位円を用いて理解する練習がてら、説明します。
角$${\theta}$$に対して、$${180-\theta}$$を考えます。$${0°<\theta<180°}$$
このとき、
$${sin(180-\theta)=sin\theta}$$
$${cos(180-\theta)=-cos\theta}$$
$${tan(180-\theta)=-tan\theta}$$
が成り立ちます。
単位円を描いて考えると、

$${∠POA=\theta,∠QOA=180°-\theta}$$とすると、
$${P(cos\theta,sin\theta),Q(cos(180°-\theta),sin(180°-\theta))}$$である。
$${∠QOB=\theta}$$となる。
このとき、$${△POA,△QOB}$$において
$${∠POA=∠QOB=\theta}$$
$${∠PAO=∠QBO=90°}$$
$${PO=QO}$$だから、
$${△POA≡△QOB}$$
$${AO=BO,PA=QB}$$となるから、図より
$${Q(-cos\theta,sin\theta)}$$となる。
よって、$${sin(180°-\theta)=sin\theta,cos(180°-\theta)=-cos\theta}$$
また、$${PO,QP}$$の傾きに注目すれば、
$${tan(180-\theta)=-tan\theta}$$は明らかに成り立ちます。
他にも、$${90°-\theta}$$や$${180°+\theta}$$などがあるので、単位円を使って自分で導出してみてくださいね。
あとは、三角形の面積の公式や余弦定理などがありますが、教科書みれば理解できる(そこまで難解ではない)ので割愛します。
決してめんどくさいわけではありません。決して。
確率統計
いよいよ、最後の確率統計に入ります。ここでは、確率の本質であり理解が困難でもある、同様に確からしいについて話していきます。
同様に確からしいとは
単純に言えば、すべての事象の起こりやすさが等しいことです。
例えば、さいころを1回投げるとき、1の目が出る確率は$${\frac{1}{6}}$$です。
ただ、この結果を一度立ち止まって考えてみます。この$${\frac{1}{6}}$$とはいったい何なのか。
さいころの目の出方について考えると、目は1~6の6通りです。だから、そのの中で1の目がでる場合は1通りだから$${\frac{1}{6}}$$だ!
、、、と考えると確率の本質はつかめません。
↑の考え方には、考慮していない点があります。それこそ同様に確からしいか?ということです。
実際さいころの目の出方は同様に確からしいので、$${\frac{1}{6}}$$で正解です。ただし例えば、とんでもないイカサマさいころがあったとして、1の目だけ非常に出やすくなっていたとしましょう。この場合も、$${\frac{1}{6}}$$としていいのでしょうか。答えはNOです。なぜなら同様に確からしくないから。言い換えれば、全ての事象の起こり方が平等でないからです。
ここで、同様に確からしいことを図で考えてみます。さいころを例に出すと、全ての事象は6通りあって、それらは平等に起こりやすいので、正方形が6個で構成された長方形をイメージします。

それぞれの正方形は面積が同じように考えると、赤色と全体(一の目が出る事象を表す)の面積比は$${1:6}$$となり、赤色の面積の割合は$${\frac{1}{6}}$$です。ちゃんと確率と一致しました。
では、1の目が出やすいイカサマさいころは、どのようなイメージなのでしょうか。
面積で考えると、1の目が出る(=赤色)が大きいわけなので、

例えば↑のように考えると、赤色の面積の割合は$${\frac{4}{9}}$$となり、$${\frac{1}{6}}$$と不一致になります。
なぜこのような結果になったのか。それは、起こりうる事象が同様に確からしくないからです。
あからさまに、赤色の面積(一の目が出る)が大きくなっています。この状態で、「全パターン6通りのうちの1通りだから$${\frac{1}{6}}$$」と考えるのはおかしいというのは、これで理解できたと思います。
今までの話でこう考えた人もいるかもしれません。
確率って面積比じゃないの???
答えを言えば、「うまく落とし込めたら」YES です。
うまく落とし込むためには、同様に確からしいことの理解はしておかないといけませんが。
ただ、面積比の考えを使えば、少し楽に確率の問題を解くこともできます。
例えば、このような問題
1,2,3の数字を重複を許して2個取り出し、順に十の位、一の位として2桁の整数を作るとき、それが偶数となる確率を求めよ。
数字の取り出し方は$${3^2=9}$$通り
整数が偶数となるとき、1の位が2の倍数であればよいから、
一の位は2だけで1通り。それに対し、十の位は1,2,3の三通り。
よって確率は、$${\frac{1*3}{9}=\frac{1}{3}}$$
これを図でイメージすると、以下のようになります。

赤色の面積の割合は、$${\frac{1*3}{9}=\frac{1}{3}}$$となり、確率と一致します。(各ブロックは正方形です)
ただこの図をよく見ると、縦3ブロックを一つの長方形とみることができるので、

↑の図のようになり、直接$${\frac{1}{3}}$$と求められます。
三つの長方形は面積が等しいので、この三つの事象は同様に確からしいと考えられます。
ちなみに、この図が何を表しているかというと、今回の問題では一の位でどんな数が出るかは、他の試行に影響しない(=独立な試行)ので、一の位だけを考えればよい。
一の位の出方は1,2,3で三通り
偶数の数は2の一通り
よって、$${\frac{1}{3}}$$と求められます。
当たり前といえばそうですが、この考え方、原理を意識的に理解することでほかの難解な問題にも対応することができます。
(ちなみに)
同様に確からしい について、違和感を覚えませんか?
なぜ数学という厳密性が重要視される学問に、~らしいとついているのでしょうか。同様に確かである、でもいい気がします。
これは、正確に言えば同様に確かであるかはわからないけど、何度試しても事象が平等に起こるから、確かであることにしておこう、、、これを省略して同様に確からしいと呼んでいるのです。
3.数学の勉強法
最後に、実際どのように勉強していけばよいか解説して、今回の話を終わりたいと思います。
結論から言えば、
(i) 解説を熟読する
(ii) 時間をかけまくって考える
(iii)積極的に数学に触れる
の三つが大事です。
解説を熟読する
数学の能力はどんな時に成長するか。それは、問題を解いた時ではなく、新たな解き方や考え方を身に着けた時です。
既に知っている方法を繰り返していても、確かに練度は上がるかもしれませんが伸びません。では、どうしたら新しく知識を得ることができるのか、それこそが解説の熟読です。
皆さんが問題集を解くとき、答えがあってたら〇にしてませんか?正確には答え”だけ”みて、正誤を判断しているようでは数学の成績は伸びるわけがありません。自分のやり方があっているのかどうか。違ったやり方であっても、正しいのか正しくないのか。その場合の模範解答の解き方はどんな問題に適応することができるのか、、、そうした情報が、解答から読み取すことができます。
これをするかしないかでは雲泥の差です。今日からでも解説はちゃんと読みましょう。
意識としては、問題を解く時間より解説を読む時間のほうが多くなるってぐらい、解説を大切にして下さい。
ちなみに、私が時々「〇〇(某数学問題集)はクソ」と言っていますが、そんな問題集の共通点は解説が少ないということです。解説に重きを置いていない問題集は滅んでもいいと思うんですけどね、、、。
時間をかけまくって考える
よく、数学の勉強法で「問題をたくさん解く」と言われますが、簡単な問題をたくさんやっても正味意味ないし、同じ問題だけやってもあまり効果は期待できないと思ってきます。実際の入試では、見たことのない問題が当たり前のように出る世界ですから、当然初見問題へ対応することが求められます。
それの対策は、やはり考える力を身に着けることです。どんな難しい問題でも、解説さえ見れば基本は理解できるようになっています。何時間もかければいけますよ。
その時間を惜しんでしまうのはもったいないです。何時間でもかけて、自分の中で答えを出した経験は、何十問の問題を解くより価値がある気もします。
とにかく考える、これが大切です。
積極的に数学に触れる
例えば、授業で公式を教えられたとき、私が真っ先に行うのは導出です。
なぜその公式が成り立つのか、その公式の意義は何なのか。それを自分だけの力でまずは答えを出す。そうした積極的な姿勢が、数学力の成長には欠かせません。
積極的、具体的に言えばなぜそうなるのかを自ら考える態度をもって数学に向き合うと、数学の根本的な印象が変わります。
今すぐにでもできるのは公式の導出です。もちろん、習った段階ではできないものもありますが、できる範囲で導出しようとすることで、その公式の見え方が変わったり、導出の過程が役に立つツールになったりといいことだらけです。
さいごに
今回は、数学の単元解説や勉強法について話しました。
大切な内容をピックアップして書いたので、もちろん書けなかったこともありますが、それはまた別の記事で書いていきます。
数学は、一度苦手意識がついてしまうと中々抜け出すことが難しい教科です。苦手な人で共通しているのは、やはり基礎が脆弱であることだと思います。この記事に限らず、基礎を固めることは最重要です。そして、そのためには解説の存在は欠かせません。
私がどうしても皆さんに求めたいのは、解説の重要性を理解することです。それが、数学の世界をより明るく楽しいものにしてくれると、私は確信しています。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
