
シリーズPython⑨ はじめての統計的因果推論を少々Pythonで
はじめに
はじめての統計的因果推論の紹介
この記事は書籍「はじめての統計的因果推論」(岩波書店、以下「テキスト」と呼びます)の一部をPythonで実践したことを取り扱います。
テキストは2024年3月に発売され、その名の通り、はじめて統計的因果推論を学ぶ初学者のための優しくてほどほどに詳しい書籍です。
統計的因果推論の第一歩にこのテキストを選んで大正解!と私は感じています。
フレンドリーな例題と選びぬかれたわかりやすい表現のおかげで、難解なバックドア基準や共変量セットのバランシング手法を「ふんわりと」読み解くことができました。
プログラムコードに話題を移します。
テキストはプログラム言語を掲載していませんが、随所に統計・計算処理が行われていて、R を使っているかな?と感じる箇所がありました。
(グラフ描画は ggplot2?、とか)
だったらコードを書いてみよう!ということで、テキストの中から気になった2つのテーマを拾い出してPythonで動かしてみました。

まえがき
この記事は、出典に記載の書籍に掲載された文章及びデータを引用し、適宜、掲載文章を改変して書いています。
Python のコードは趣味的に作成されたものであり、テキストの著者の意図を反映したものではなく、処理の正確性は担保しておりません。
誤りや改善点がありましたら、ぜひ教えてください。
【出典】
「はじめての統計的因果推論」(第1刷、林岳彦 著、岩波書店)
第4章 共変量に着目
テキストの第4章では、共変量
■ コード化の対象
4.3節「重回帰分析で揃える」および巻末補遺A1「共変量Cの影響に対する"補正計算"としての重回帰」に掲載のグラフ、単回帰・重回帰の結果を扱います。
単回帰・重回帰分析には statsmodels の ols を利用します。

1.インポート
### インポート
# 基本
import pandas as pd
import numpy as np
# 統計処理
import statsmodels.formula.api as smf
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの登録
テキストのデータをお借りします。
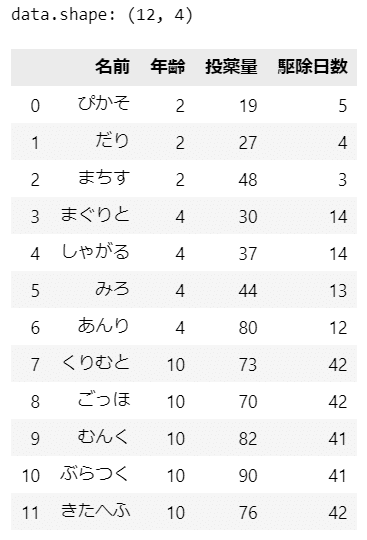
### データの登録 ★テキスト表4.4のデータを引用
# 変数の設定
names = ['ぴかそ', 'だり', 'まちす', 'まぐりと', 'しゃがる', 'みろ', 'あんり',
'くりむと', 'ごっほ', 'むんく', 'ぶらつく', 'きたへふ']
ages = [2, 2, 2, 4, 4, 4, 4, 10, 10, 10, 10, 10]
treats = [19, 27, 48, 30, 37, 44, 80, 73, 70, 82, 90, 76]
days = [5, 4, 3, 14, 14, 13, 12, 42, 42, 41, 41, 42]
# データフレーム化
data = pd.DataFrame({
'名前': names, '年齢': ages, '投薬量': treats, '駆除日数': days})
# 結果表示
print('data.shape:', data.shape)
display(data)【実行結果】
猫の名前、年齢(共変量
「きたへふ」って誰?(北別府投手?)
3.要約統計量
テキストに掲載の各変数の平均値を表示します。
### 平均値の表示 ★テキスト137ページ
data.iloc[:, 1:].mean(axis=0).to_frame().T.set_axis(['平均'], axis=0).round(2)【実行結果】

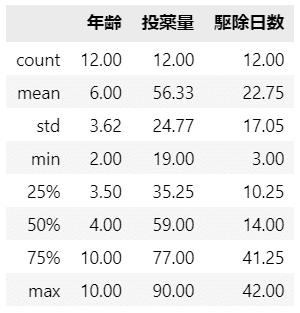
要約統計量も見ておきましょう。
### 要約統計量の表示
data.describe().round(2)【実行結果】
4.散布図と相関関係
相関係数をざっと眺めて、テキスト掲載の散布図を描いてみましょう。
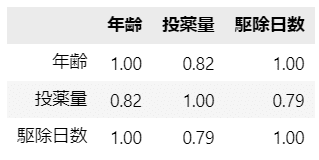
### 相関行列の表示
data.corr(numeric_only=True).round(2)【実行結果】
全変数間で強い相関関係が見られます。
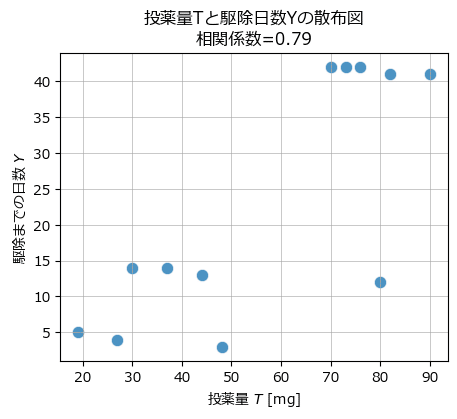
投薬量
テキストの図4.7左に相当します。
### 散布図の描画1 ★図4.7左
# 描画領域の設定
fig, ax = plt.subplots(figsize=(5, 4))
# 散布図の描画
sns.scatterplot(data=data, x='投薬量', y='駆除日数', s=80, ec='white', alpha=0.8,
ax=ax)
# 修飾
ax.set(xlabel='投薬量 $T$ [mg]', ylabel='駆除までの日数 $Y$',
title=f"投薬量Tと駆除日数Yの散布図\n"
f"相関係数={data[['投薬量', '駆除日数']].corr().iloc[0, 1]:.2f}")
ax.grid(lw=0.5);【実行結果】
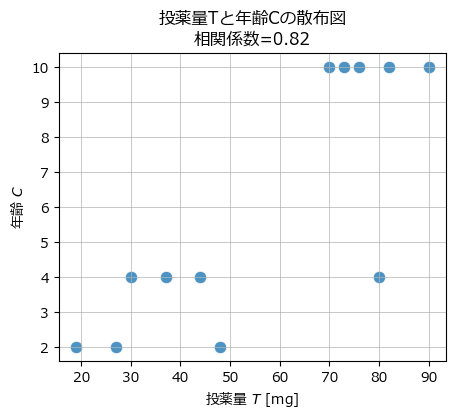
続いて投薬量
テキストの図4.7右に相当します。
### 散布図の描画2 ★図4.7右
# 描画領域の設定
fig, ax = plt.subplots(figsize=(5, 4))
# 散布図の描画
sns.scatterplot(data=data, x='投薬量', y='年齢', s=80, ec='white', alpha=0.8,
ax=ax)
# 修飾
ax.set(xlabel='投薬量 $T$ [mg]', ylabel='年齢 $C$',
title=f"投薬量Tと年齢Cの散布図\n"
f"相関係数={data[['投薬量', '年齢']].corr().iloc[0, 1]:.2f}")
ax.grid(lw=0.5);【実行結果】
投薬量:処置
5.単回帰
目的変数:駆除日数
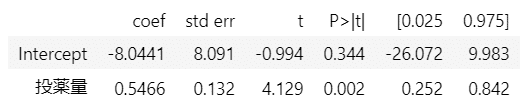
テキストの137ページに掲載があります。
### 単回帰 ★テキスト137ページ βhat=0.55
result1 = smf.ols(formula='駆除日数 ~ 投薬量', data=data).fit()
result1.summary().tables[1]【実行結果】
投薬量の回帰係数は
いっけん統計的に有意な回帰係数に見えています。
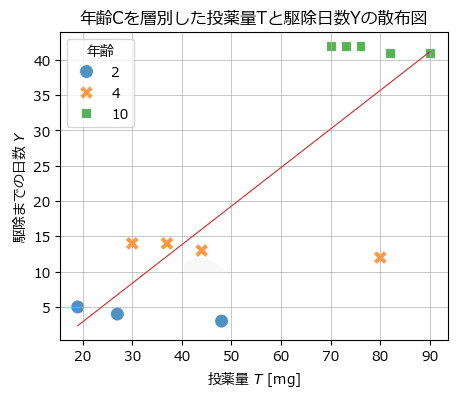
見せかけの回帰を確認すべく、年齢
テキストの図4.8に相当します。
### 散布図の描画3 ★図4.8
# 描画領域の設定
fig, ax = plt.subplots(figsize=(5, 4))
# 年齢を層別した散布図の描画
sns.scatterplot(data=data, x='投薬量', y='駆除日数',
hue='年齢', palette='tab10',
style='年齢', s=100, ec='white', alpha=0.8, ax=ax)
# 回帰直線の描画
sns.regplot(data=data, x='投薬量', y='駆除日数', scatter=False, ci=None,
color='tab:red', line_kws={'lw': 0.8}, ax=ax)
# 修飾
ax.set(xlabel='投薬量 $T$ [mg]', ylabel='駆除までの日数 $Y$',
title='年齢Cを層別した投薬量Tと駆除日数Yの散布図')
ax.grid(lw=0.5);【実行結果】
年齢が投薬量と駆除日数に影響していました。
6.重回帰
年齢:共変量
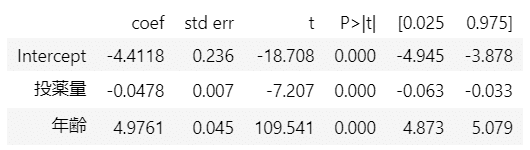
テキストの138ページに掲載があります。
### 重回帰 ★テキスト138ページ βThat=-0.048
result2 = smf.ols(formula='駆除日数 ~ 投薬量 + 年齢', data=data).fit()
result2.summary().tables[1]【実行結果】
投薬量
7.重回帰結果を用いた補正
話題は巻末補遺A1に移ります。
年齢
年齢の平均値からの差分に年齢の偏回帰係数
テキストの表A1.1に相当します。
### 年齢による駆除日数の補正 ※平均年齢差にかかる駆除日数を加減算 ★表A1.1
data['補正後日数'] = data.apply(
lambda x: x['駆除日数'] + -4.98 * (x['年齢'] - data['年齢'].mean()), axis=1)
display(data)【実行結果】
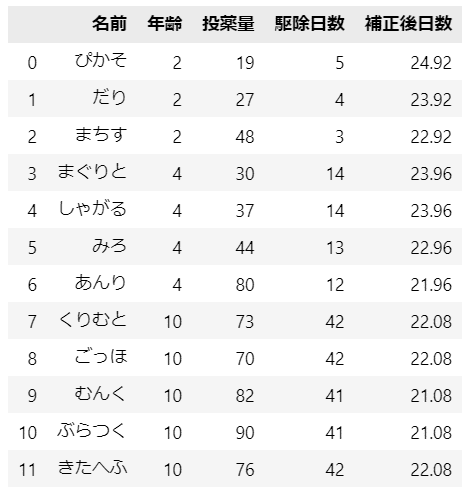
あわせて各変数の平均値を表示します。
### 平均値の表示 ★表A1.1の平均値
data.iloc[:, 1:].mean(axis=0).to_frame().T.set_axis(['平均'], axis=0).round(2)【実行結果】

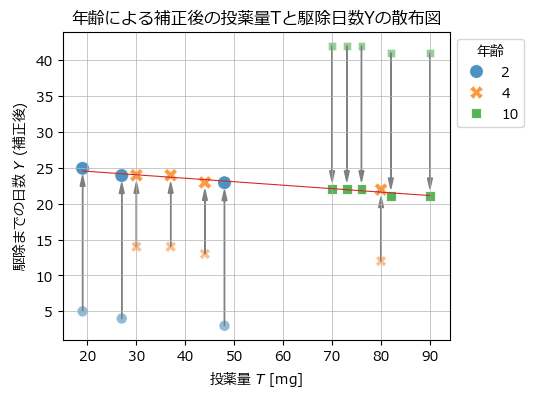
最後に年齢による影響の補正を散布図で表現したテキストの図A1.1下を描画します。
(この図を描きたくてPython化を始めました!)
### 散布図の描画4 ★図A1.1
# 描画領域の設定
fig, ax = plt.subplots(figsize=(5, 4))
# 補正前の駆除日数の散布図の描画
sns.scatterplot(data=data, x='投薬量', y='駆除日数', hue='年齢', palette='tab10',
style='年齢', s=60, ec='white', alpha=0.5, legend=False, ax=ax)
# 補正後の駆除日数の散布図の描画
sns.scatterplot(data=data, x='投薬量', y='補正後日数', hue='年齢', palette='tab10',
style='年齢', s=100, ec='white', alpha=0.8, ax=ax)
# 補正後の駆除日数に基づく回帰直線の描画
sns.regplot(data=data, x='投薬量', y='補正後日数', scatter=False, ci=None,
color='tab:red', line_kws={'lw': 0.8}, ax=ax)
# 矢印線の描画
for i in range(len(data)):
startx, starty = data.loc[i, '投薬量'], data.loc[i, '駆除日数']
lengthy = (data.loc[i, '補正後日数'] - data.loc[i, '駆除日数'])
lengthy = lengthy - np.sign(lengthy) * 2.5
ax.arrow(startx, starty, 0, lengthy, head_width=1, head_length=1.5,
fc='gray', ec='gray')
# 修飾
ax.set(xlabel='投薬量 $T$ [mg]', ylabel='駆除までの日数 $Y$ (補正後)',
title='年齢による補正後の投薬量Tと駆除日数Yの散布図')
ax.legend(bbox_to_anchor=(1, 1), title='年齢')
ax.grid(lw=0.5);【実行結果】
薄い点が補正前、濃い点が補正後です。
矢印の方向に補正されています。
赤い線は投薬量
補正後の駆除日数を目的変数にして単回帰分析を行ってみます。
テキストの250ページに掲載があります。
### 補正後の日数で単回帰 ★テキスト250ページ βhat=-0.048
result3 = smf.ols(formula='補正後日数 ~ 投薬量', data=data).fit()
result3.summary().tables[1]【実行結果】
投薬量

第4章のPythonの旅は以上です。
一息つきましょう。

第5章 「次元の呪い」の罠の外へ
テキストの第5章では「傾向スコア法」を学びます。
傾向スコア法は、共変量
回帰モデルに関するテキストの式をお借りします。
ロジスティック回帰によるモデルです。
T = \cfrac{\beta_0 + \beta_1 C_1 + \cdots + \beta_KC_K}{1+\exp(-(\beta_0 + \beta_1 C_1 + \cdots + \beta_KC_K))}
傾向スコアの推定値
ロジスティック回帰で得られたパラメータ
\hat{e}_i = \cfrac{\hat{\beta}_0 + \hat{\beta}_1 C_1^i + \cdots + \hat{\beta}_K C_K^i}{1+\exp[-(\hat{\beta_0} + \hat{\beta_1} C_1^i + \cdots + \hat{\beta_K} C_K^i)]}
■ コード化の対象
5.2節「傾向スコア法を使ってみよう」、5.3節「傾向スコアによるマッチング」に掲載の傾向スコアの計算、マッチングを実践します。
ロジスティック回帰分析には statsmodels の logit を利用します。

1.インポート
### インポート
# 基本
import pandas as pd
import numpy as np
# 統計処理
import statsmodels.formula.api as smf
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'2.データの登録
テキストのデータをお借りします。
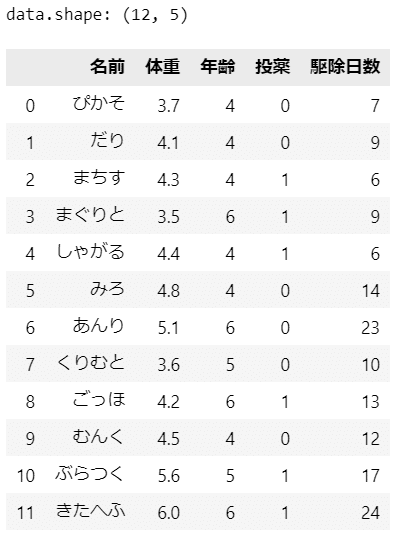
### データの登録 ★テキスト表5.1のデータを引用
# 変数の設定
names = ['ぴかそ', 'だり', 'まちす', 'まぐりと', 'しゃがる', 'みろ', 'あんり',
'くりむと', 'ごっほ', 'むんく', 'ぶらつく', 'きたへふ']
weights = [3.7, 4.1, 4.3, 3.5, 4.4, 4.8, 5.1, 3.6, 4.2, 4.5, 5.6, 6.0]
ages = [4, 4, 4, 6, 4, 4, 6, 5, 6, 4, 5, 6]
treats = [0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1]
days = [7, 9, 6, 9, 6, 14, 23, 10, 13, 12, 17, 24]
# データフレーム化
data = pd.DataFrame({
'名前': names, '体重': weights, '年齢': ages, '投薬': treats,
'駆除日数': days})
# 結果表示
print('data.shape:', data.shape)
display(data)【実行結果】
猫の名前、体重と年齢(共変量
3.要約統計量
テキストの表5.1に掲載の各変数の平均値を表示します。
### 平均値の表示 ★表5.1の集計行
data.iloc[:, 1:].mean(axis=0).to_frame().T.set_axis(['平均'], axis=0).round(2)【実行結果】

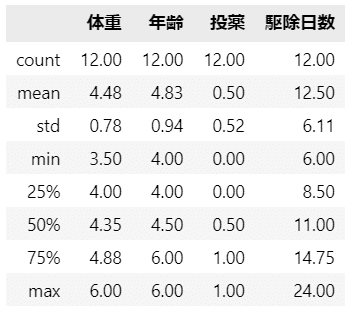
要約統計量も見ておきましょう。
### 要約統計量の表示
data.describe().round(2)【実行結果】
4.傾向スコアの推定
目的変数:投薬の有無
### 処置Tと共変量Cのロジスティック回帰の実行 statsmodelsのlogit
result1 = smf.logit(formula='投薬 ~ 体重 + 年齢', data=data).fit()
result1.summary().tables[1]【実行結果】
体重の係数が

続いて傾向スコアを推定します。
ロジスティック回帰の結果変数 result1 に対して predict() を行うことで、処置の有無の確率の予測値=傾向スコアを得られます。
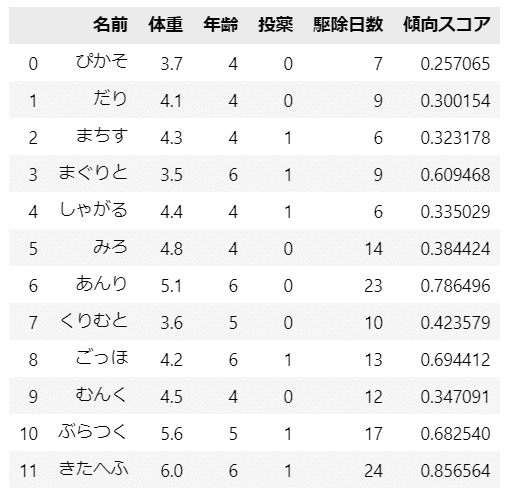
### 傾向スコアの算出 ※predict()で逆logit変換後の値を得られる ★表5.2
data['傾向スコア'] = result1.predict()
display(data)【実行結果】
案外あっさりと傾向スコアを算出できました。
(参考)
次のコードは、推定した係数・切片に各個体の説明変数値を当てはめる方法で計算しています。
### 線形予測子を逆logit変換して算出(xはresult.fittedvaluesでも取得可能)
# 傾向スコア算出関数の定義 row:行, result:logit回帰の結果
def calc_score(row, result):
intercept, coef_weight, coef_age = result.params
x = intercept + coef_weight * row['体重'] + coef_age * row['年齢']
return 1 / (1 + np.exp(-x)) # np.exp(x) / (1 + np.exp(x)) と同じ
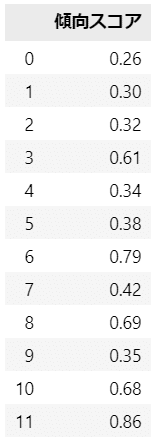
# 傾向スコアの算出
(data.apply(calc_score, args=(result1,), axis=1).to_frame()
.set_axis(['傾向スコア'], axis=1).round(2))【実行結果】
5.傾向スコアによるマッチング
テキストにならって「復元あり・重み付けなしの最近隣法マッチング」を行ってみます。
テキストの表5.3に相当します。
### 傾向スコア・マッチング ※復元あり・重み付けなしの最近隣法マッチング
## マッチング用データの作成
# 投薬ありT=1となしT=0に分割, 列名にT1,T0を付与して識別
T1 = data[data['投薬']==1].set_axis([f'{c}T1' for c in data.columns], axis=1)
T0 = data[data['投薬']==0].set_axis([f'{c}T0' for c in data.columns], axis=1)
## 傾向スコア・マッチング処理
T0_match = pd.DataFrame()
# 投薬ありT1の傾向スコアに最も近い投薬なしT0を取得
for T1idx in T1.index:
# 傾向スコアの差の絶対値が最も小さい投薬なしT0の行インデックス値を取得
T0idx = abs(T0['傾向スコアT0'] - T1.loc[T1idx, '傾向スコアT1']).idxmin()
# マッチングした順にT0をT0_matchデータフレームに追加格納
T0_match = pd.concat([T0_match, T0[T0.index==T0idx]], axis=0)
# T1とマッチングしたT0とを1つのデータフレームに結合
matching_df = pd.concat([T1.reset_index(drop=True),
T0_match.reset_index(drop=True)], axis=1)
# 駆除日数の差分列の追加
matching_df['駆除日数差'] = matching_df['駆除日数T1'] - matching_df['駆除日数T0']
# 平均行の追加
matching_df.loc['平均'] = matching_df.mean(numeric_only=True)
## データフレームの表示
display(matching_df.round(2))【実行結果】
左側に処置ありデータ、右側にマッチングした処置なしデータを並べて、最右列に駆除日数の差(Yの差分)を作成しました。
傾向スコアマッチングによる共変量のバランシング後の因果効果は

おわり

ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
