
数学とPython 3 三角形の外接円と内接円 ~ 距離・可視化
はじめに
シリーズ数学とPythonのご案内
「シリーズ数学とPython」は、数学の学習中に「解けない、無理~」と焦ったときに、Pythonで数値の動きや可視化を行って、理解の糸口を見つけたときのことを記事にします。
データサイエンス数学ストラテジスト上級公式問題集
この記事は「データサイエンス数学ストラテジスト上級公式問題集」の問題の解読中に見つけたヒントを取り扱います。
今回取り組む問題
問題21「三角形の外接円と内接円の半径の比を求めよう!」
Python実装
やりたいこと
問題文で与えられた三角形の2辺の長さと1角に基づいて、三角形・外接円・内接円を描画します。
作戦
こちらのWebサイトから、3点の座標に基づいて外接円・内接円の中心座標と半径を算出する関数を拝借します。
ありがとうございます!
実装の開始
インポート
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import patches
plt.rcParams['font.family'] = "MS Gothic"関数の定義
お借りした関数の定義です。
### 外接円の中心座標(x,y)と半径rを算出する関数
# 引数:三角形の頂点の座標
def circumcircle(P1, P2, P3):
x1, y1 = P1; x2, y2 = P2; x3, y3 = P3
a = 2*(x1 - x2); b = 2*(y1 - y2); p = x1**2 - x2**2 + y1**2 - y2**2
c = 2*(x1 - x3); d = 2*(y1 - y3); q = x1**2 - x3**2 + y1**2 - y3**2
det = a*d - b*c
x = d*p - b*q; y = a*q - c*p
if det < 0:
x = -x; y = -y; det = -det
x /= det; y /= det
r = ((x - x1)**2 + (y - y1)**2)**.5
return x, y, r
### 内接円の中心座標(x,y)と半径rを算出する関数
# 引数:三角形の頂点の座標
# 内接円の半径=2×三角形の面積/3辺の長さの和
def incircle(P1, P2, P3):
x1, y1 = P1; x2, y2 = P2; x3, y3 = P3
dx1 = x2 - x1; dy1 = y2 - y1
dx2 = x3 - x1; dy2 = y3 - y1
d1 = ((x3 - x2)**2 + (y3 - y2)**2)**.5
d2 = (dx2**2 + dy2**2)**.5
d3 = (dx1**2 + dy1**2)**.5
dsum = d1 + d2 + d3
r = abs(dx1 * dy2 - dx2 * dy1) / dsum
x = (x1*d1 + x2*d2 + x3*d3) / dsum
y = (y1*d1 + y2*d2 + y3*d3) / dsum
return x, y, r設定と sin B , cos B の計算
問題で与えられた辺$${a,c}$$の長さ及び$${\angle \text{ABC}}$$の角度を設定して、$${\sin B,\ \cos B}$$を計算します。
$${\cos B,\ \sin B}$$の計算はNumPyの cos、sin を利用します。
引数にラジアンを与える必要があり、角度からラジアンへの変換をNumPyの radians で行います。
おまけコードでは、余弦定理$${b^2=a^2+c^2-2ac\cos B}$$を用いて残りの辺$${b}$$の長さを計算しています。
### 問題の残りの辺b(=AC)の長さを余弦定理で算出
# 設定
c, a = 8, 5 # 辺c(AB),a(=BC)の長さ
angle_B = 60 # ∠ABCの角度
# 三角関数の値の取得
cos_B = np.around(np.cos(np.radians(angle_B)), 10)
sin_B = np.around(np.sin(np.radians(angle_B)), 10)
### おまけ:b(=AC)の辺の長さの計算
# 余弦定理b^2 = a^2 +c^2 -2ac cosBの平方根
b = np.sqrt(a**2 + c**2 - 2*a*c*cos_B)
print('辺b(AC)の長さ: ', b)三角形・外接円・内接円の描画
はじめに3点の座標を設定します。
このコードでは、次のことを前提にしています。
・点Bの座標[x_B, y_B]は、パラメータで設定します。
・点Cの座標は点Bからx軸方向に平行移動した点とします。
・点Aの座標は∠ABCから求めます。
# 点Bの座標の設定
x_B, y_B = 0, 0
# 点A、B、Cの算出(辺BCはx軸に水平)
node_B = (x_B, y_B)
node_A = (c * cos_B + x_B, c * sin_B + y_B)
node_C = (x_B + a, y_B)
print(f'点A{node_A}, 点B{node_B}, 点C{node_C}')
いよいよ描画処理です!
##### 三角形、外接円、内接円の描画
### 三角形の頂点の座標を基にして、外接円・内接円の中心座標と半径の取得
p1, p2, p3 = node_A, node_B, node_C
x_ci, y_ci, r_ci = circumcircle(p1, p2, p3) # 外接円
x_in, y_in, r_in = incircle(p1, p2, p3) # 内接円
### 描画
fig, ax = plt.subplots(figsize=(6, 6))
tri, cicir, incir = 'steelblue', 'green', 'red' # 色:三角形、外接円、内接円
# 三角形の描画
node = np.array([p1, p2, p3])
ax.plot(np.hstack([node[:, 0], node[0, 0]]),
np.hstack([node[:, 1], node[0, 1]]), c=tri)
# ax.scatter(node[:, 0], node[:, 1], c=tri)
# 外接円の描画
patch = patches.Circle(xy=(x_ci, y_ci), radius=r_ci, fill=False, ec=cicir)
ax.add_patch(patch)
ax.scatter(x_ci, y_ci, c=cicir, s=15) # 中心点の描画
# 内接円の描画
patch = patches.Circle(xy=(x_in, y_in), radius=r_in, fill=False, ec=incir)
ax.add_patch(patch)
ax.scatter(x_in, y_in, c=incir, s=15) # 中心点の描画
# 修飾
ax.set_aspect('equal')
ax.text(p1[0], p1[1]+0.1, 'A', size=15)
ax.text(p2[0]-0.3, p2[1]-0.4, 'B', size=15)
ax.text(p3[0], p3[1]-0.4, 'C', size=15)
plt.title(f'三角形の頂点 A:({p1[0]:.1f}, {p1[1]:.1f}) '
f'B:({p2[0]:.1f}, {p2[1]:.1f}) '
f'C:({p3[0]:.1f}, {p3[1]:.1f})\n'
f'外接円の中心({x_ci:.1f}, {y_ci:.1f}), '
f'内接円の中心({x_in:.1f}, {y_in:.1f})')
plt.show()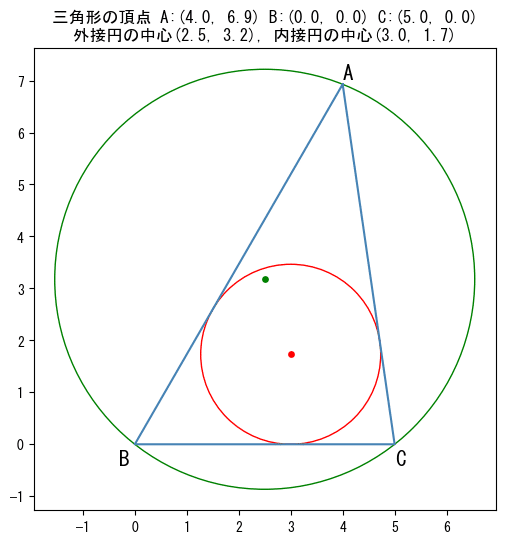
三角形、外接円(緑の円)、内接円(赤い円)を描くことができました!
グラフの上部には、三角形の3点の座標、外接円の中心座標、内接円の中心座標を表示しています。
【コードの補足】
・三角形は折れ線グラフ(plot)で3点を結んでいます。
・円は matplotlib の patches.Circle を利用しています。
引数は次のとおり。
・xy:中心座標(x, y)
・radius:半径
・fill=False:塗りつぶししない
・ec:円周の線の色
辺の長さの検算
グラフの三角形が適切かどうか確認する目的で、3点の座標から三角形の辺の長さを計算して検算しましょう。
2点$${[x_1, y_1],[x_2, y_2]}$$について、$${\sqrt{(x_1-x_2)^2+(y_1- y_2)^2}}$$を計算します。
### 3座標つの座標から辺の長さを求めて検算
a_calc = np.sqrt((node_B[0]-node_C[0])**2 + (node_B[1]-node_C[1])**2)
b_calc = np.sqrt((node_A[0]-node_C[0])**2 + (node_A[1]-node_C[1])**2)
c_calc = np.sqrt((node_A[0]-node_B[0])**2 + (node_A[1]-node_B[1])**2)
print(f'辺の長さの検算: AB={c_calc:.1f}, BC={a_calc:.1f}, AC={b_calc:.1f}')
3辺の長さが合っているので、3点の座標は適切です!
外接円・内接円という言葉自体、この問題集で初めて知りました。
描いてみて、三角形・外接円・内接円が身近な存在になりました!
可視化できてよかったです!
(数式と比べて優しい温もりを感じます😉)
おわりに
平面の座標を特定して、長さを測り、描画をすることは、数学的な知識とPythonの可視化ライブラリの知識が必要です。
2つの知識が乏しくて、図形の描画につまずき、つまずきながら、Webサイトで関連情報を収集して、なんとか、図形を描くことができました。
おわり
ブログの紹介
noteで3つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
3.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
この記事が気に入ったらサポートをしてみませんか?
