
「数値シミュレーションで読み解く統計のしくみ」をPythonで写経 ~ 第2章2.1「言語の基礎」
第2章「プログラミングの基礎」
書籍の著者 小杉考司 先生、紀ノ定保礼 先生、清水裕士 先生
この記事は、テキスト「数値シミュレーションで読み解く統計のしくみ」第2章「プログラミングの基礎」2.1節「言語の基礎」および2.2節「オブジェクトと変数の種類」の Python写経活動 を取り扱います。
今回からの3記事はシミュレーションの準備体操にあたります。
R の基本的なプログラム記法はざっくり Python の記法と近いです。
コードの文字の細部をなぞって、R と Python の両方に接近してみましょう!
ではテキストを開いて準備体操の旅に出発です🚀

はじめに
テキスト「数値シミュレーションで読み解く統計のしくみ」のご紹介
このシリーズは書籍「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」(技術評論社、「テキスト」と呼びます)の Python写経です。
テキストは、2023年9月に発売され、副題「Rでためしてわかる心理統計」のとおり、統計処理に定評のある R の具体的なコードを用いて、心理統計の理解に役立つ数値シミュレーションを実践する素晴らしい書籍です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」初版第1刷、著者 小杉考司・紀ノ定保礼・清水裕士、技術評論社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
2.1 言語の基礎
テキストはシミュレーションの基礎になる「Rによるプログラミング」に慣れることを目標にして、初歩的なコードを R で書いています。
この記事は Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
今回取り組む R のコード・構文は Python とよく似ています。
2.1.1 最初の計算
足し算のプログラミングです。
Python のコードは R のコードと同じです。
### 12ページ
1 + 2【実行結果】
電卓の代用!
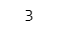

2.2 オブジェクトと変数の種類
2.2.1 オブジェクト
「オブジェクト」の概念を語るにはこの記事のスペースでは難しいです。
R では「<-」と表現することを Pythonでは「=」にします。
ひとまず、イコール(=)の左側が「器」(この記事では変数と呼びます)、右側が入れたい内容、という風に思ってください。
数字の変数 a, b に慣れましょう。
### 13ページ 数字
a = 1
b = 2
a + b【実行結果】
aが3、bが2ですので、a+b は 1+2 となり、答えは 3 です。
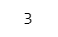
続いて文字の変数に慣れましょう。
### 13ページ 文字列
msg = 'Hello World!'
msg【実行結果】
1行目は msg という器(変数)に Hello World! という言葉を入れています。
2行目は msg の中身を見せてくださいというコードです。
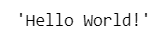
つづいて、テキストは「変数名」の違いにフォーカスします。
### 13ページ 変数名は大文字・小文字で区別できる
a = 2
b = 2
A = 5
a * b【実行結果】
ポイントは「a」と名付けた変数と「A」と名付けた変数が別物だよ、って点です。
「*」は掛け算の記号なので、a * b → 2 × 2 = 4 になります。
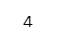
今度は A を使います。
### 14ページ (続き)
A + b【実行結果】
A + b → 5 + 2 = 7 です。
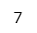
今度は a の中身を書き換えます。
### 14ページ 上書きする
a = 2
a + b【実行結果】
1行目で a の中身が 2 に変わりました。
そうすると、a + b = 2 + 2 = 4 です。
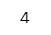
また a の中身を書き換えます。
### 14ページ (続き)
a = 6
a + b【実行結果】
a + b → 6 + 2 = 8 。
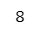
a の中身が変わる → 数が変わる → 変数!
変数は中にどんな値が入っているかを意識する必要がありそうです。
次は算数の常識を覆すプログラミングです。
## 14ページ 代入
a = a + 1
a【実行結果】
左にも右にも a が出現!
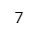
変更前の a は 6 です。右側は 変更前の a に対して + 1 です。
変更前 a + 1 = 6 + 1 = 7 となります。
先に右側を処理して、処理結果を左に入れ直している、こんな感じです。
◆ ◆ ◆ ◆ ◆
この節の最後にテキストは凄いコードを繰り出しています!
今までコツコツと値を設定した a や b などの変数全部の中身をクリア(無かったことに)するのです。
全部なかったことにする伝家の宝刀なので、システムは慎重になって、質問をしてきます。
以下のコードは Jupyter Notebook で動かした変数のクリア指示です。
## 15ページ 全変数のクリア ※Jupyter Notebookの場合のコマンド
%reset削除してしまったら変数の値を元に戻せません!
それでも削除してしまっていいですか?(Yes/No)

yを入れて削除をしてしまいます。

【実行結果】特になし
本当に消えてしまったのでしょうか?
変数 a が存在するか試してみます。
a【実行結果】
a は無い!と回答されました。消えてしまったのです。。。


2.2.2 変数の種類
Python は変数の内容によって変数の「型」と可能な処理を区別しています(たぶん)。
テキストに掲載の「内容」に沿って、変数の「基本型」を見ていきましょう。
まずは「整数」です。
### 16ページ 数値:整数型int
a = 2
type(a)【実行結果】
変数 a に 整数値 2 を入れました。
type (a) とすると、変数 a の型を確認できます。
結果は int (整数、integerの略)でした。
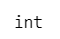
続いて「文字」です。
### 16ページ 文字列型str
b = 'Fizz'
type(b)【実行結果】
b には Fizz という文字を入れました。
「'」や「"」といったクォーテーションで文字を囲むことでPythonは「文字だ!」と認識できるようです。
type で確認した型は str (文字列、stringの略)でした。
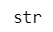
次はコンピュータならではの型です。
### 16ページ ブール型bool 真:True, 偽:False
c = True
type(c)【実行結果】
数学の「論理」に沿って、真と偽を区別する型がブール型です。
R は大文字で真:TRUE と偽:FALSE を設定しますが、Pythonでは真:True、偽:False のように表現します。
type で確認した型は bool (ブール型)でした。
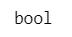
ここでテキストは変数の型の意義を分かりやすく紹介しています。
### 16ページ 文字列型に整数1を加算するとエラー
d = '3'
d + 1【実行結果】
上述のコードはエラーになります。

そして、テキストは面白い実験をしています。
前のコードで変数 c には 論理を示す TRUE が入っています。
### 17ページ ブール型に整数1を加算 Trueは1とみなされる
c + 1【実行結果】
TRUE に 1 を足すと 2 になります!
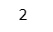
R と同様に Python もブール型に算数的な演算をすることが出来ます。
True は 1 とみなされ、False は 0 とみなされます。
c = True なので、c + 1 = 1 + 1 = 2 なのです。
このようなブール型に対する算数的な演算処理はある意味「Pythonのテクニック」として利用されることがあるので、留意しておきましょう。

2.2.3 オブジェクトの型
すでに「型」をいう用語を使っていますが、改めて、テキストの型に取り組みます。
先に整理しておきますと、R の「ベクトル」(vector)や「行列」(matrix)に直接的に対応する Python の型は無さそうです。
ですので、R を Python 化する際に、ベクトルや行列をPythonでどのように表現するかは、コード作成者の考えに委ねられています。
私個人的には、R のベクトルや行列が算術的な演算に用いられることが多そうだと見込んでいるので、numpy ライブラリの numpy 配列 ndarray を用いるのが好みです。
この記事のシリーズでは、ベクトル・行列表現になるべく numpy 配列を使おうと思っています。
ちなみに numpy には行列型の matrix が存在しますが、numpy さんが matrix の使用を推奨しないことを宣言しています。将来、matrix を削除する可能性があるということのようです。ですので、numpy の matrix は使わないようにします。
◆ ◆ ◆ ◆ ◆
では写経に戻ります。
numpyを使うにはnumpyをインポートする必要があります。
Python の慣例に従い、numpy を np と省略します。
### 17ページ numpyの配列ndarray利用
import numpy as npテキストに戻ります。
17ページの R コードの1行目から1行ずつ Python 化します。
### 17ページ 1行目 c(1, 2, 3, 4, 5, 6)
x = np.array([1, 2, 3, 4, 5, 6])
print('xの値', x)
print('xのデータ型', type(x))
print('xの値のデータ型', x.dtype)【実行結果】
1行目は x の中身の表示、2行目は変数 x の型、3行目は x の中身の型です。
2行目の numpy.ndarray は変数 x が numpy配列であることを意味します。
3行目の int32 は変数 x に入っている値 1, 2, …, 6 は整数型であることを意味します。

どんどん進みましょう。
### 17ページ 2行目 1:6
y = np.arange(1, 7) # 1~6の整数値を設定
print('yの値', y)
print('yのデータ型', type(y))
print('yの値のデータ型', y.dtype)【実行結果】
1行目が y に格納した値たちの内容です。
np.arange(1, 7) とすることで、1から6までの整数値を作り出せます。
Python の特徴は、(1, 7) のような範囲を指定するときに、終点 7 を含まないことが多い点です。

### 17ページ 3行目 c("Fizz", "Buzz")
z = np.array(['Fizz', 'Buzz'])
print('zの値', z)
print('zのデータ型', type(z))
print('zの値のデータ型', z.dtype)【実行結果】
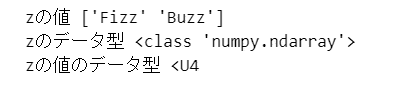
ここまでが R のベクトルに相当する numpy配列の使い方でした。
続いて R の行列に相当する numpy配列を使ってみましょう。
ベクトルに相当する x から行列を作る方法です。
### 17ページ 4行目 matrix(x, nrow=2, ncol=3) ver 1
# reshapeでxの次元を変更する。2次元に変更する場合(row, col)
A = x.reshape((2, 3)) # Rのmatrixの並び順と異なる
print('Aの値')
print(A)
print('Aのデータ型', type(A))
print('Aの値のデータ型', A.dtype)【実行結果】
Pytnon の numpy では形状変更「reshape」を用いて1次元のベクトル的な中身を2次元以上の次元に変換します。
このコードはデフォルトの行列変換です。
R の変換と値が異なることに注意しましょう。

では R と同じ変換にする方法はあるのでしょうか?
### 17ページ 4行目 matrix(x, nrow=2, ncol=3) ver 2
A = x.reshape((2, 3), order='F') # Rのmatrixの並び順と同じ
print('Aの値')
print(A)
print('Aのデータ型', type(A))
print('Aの値のデータ型', A.dtype)【実行結果】
「order='F'」を付け足して、R と同じ結果になるように工夫しました。
ちなみに F は プログラミング言語 Fortran の表現を使って!という指定です。

### 17ページ 5行目 matrix(x, nrow=3, ncol=2)
B = x.reshape((3, 2), order='F') # Rのmatrixの並び順と同じ
print('Bの値')
print(B)
print('Bのデータ型', type(B))
print('Bの値のデータ型', B.dtype)【実行結果】

テキストに沿って3次元の配列を確認しましょう。
### 18ページ 3次元配列
p = np.arange(1, 25).reshape((4, 3, 2), order='F') # Rのmatrixの並び順と同じ
print(p[:, :, 0], '\n')
print(p[:, :, 1])【実行結果】
(4, 2, 3) は、1次元目の要素数が4、2次元目の要素数が3、3次元目の要素数が2 という指定です。


オブジェクトの要素へのアクセス
Python の「スライス」と呼ばれるお作法を使います。
先ほど作成した変数 A の1行目2列目の値を取得します。
### 18ページ 行と列を指定
# pythonはインデックスが0から始まるため、Rの行・列の値より1小さい値を設定する
A[0, 1]【実行結果】
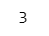
Python の特徴の1つが、配列等の各次元の番地を示すインデックスが0から始まることです。
例えば変数 A の1次元目の最初、2次元目の最初の要素は、
A[0, 0]で取得します。
続いて変数 A の1行目全体を取得します。
### 19ページ 行のみの指定
A[0, :]【実行結果】
「:」はその次元の全てを指します。
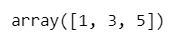
続いて変数 A の2列目全体を取得します。
### 19ページ 列のみの指定
A[:, 1]【実行結果】
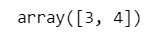

リスト型
R のリスト型に格納する要素には「名前」がつけられるのですね。
Python にもリスト型は存在しますが、要素に名前を付けられません。
### 19ページ リスト
# obj = [x, y, A] と書けます
obj = list([x, y, A])### 19ページ リストの3番めの要素Aを表示(3番目→インデックスは2)
obj[2]【実行結果】
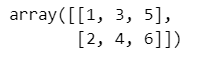
要素に名前をつける方法の1つに「辞書型」を使用があります。
辞書型は、keyと呼ばれる名前と value と呼ばれる要素の値で構成します。
### 20ページ 名前をつける場合は辞書型を活用する
# obj = {'x': x, 'vec': y, 'mat': A} とも書けます
obj = dict(x=x, vec=y, mat=A)
obj['mat']【実行結果】
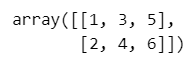
### 20ページ 辞書型のobjの全貌
obj【実行結果】
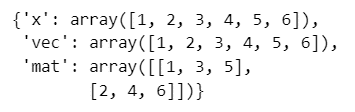
ちなみに、リストと numpy配列の使い分け法です。
変数で計算(算術的な演算)を行う場合は、numpy配列が適しています。
### リストとnumpy配列の違い
x_list = [1, 2, 3] # リスト
x_array = np.array([1, 2, 3]) # numpy配列
print('リスト :', x_list)
print('numpy配列:', x_array)【実行結果】
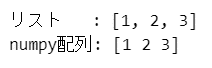
リスト x_list に1を足してみます。
### リストに1を足すとエラーになる
x_list + 1【実行結果】
エラーになりました。

numpy配列 x_array に1を足してみます。
### numpy配列に1を足すと全要素に+1する
x_array + 1【実行結果】
3つの要素に+1しました。
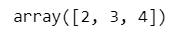
numpy配列に対して様々な演算を行えます。
例えば平均値を計算してみましょう。
### 平均
x_array.mean()【実行結果】
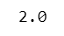

データフレーム型
R のデータフレーム型に相当するPythonの型は、Pandasライブラリの DataFrame です。データフレームです。
pandasを使うにはpandasをインポートする必要があります。
Python の慣例に従い、pandas を pd と省略します。
### 20ページ pandasのデータフレームを利用
import pandas as pdテキストの用例に沿って、pandas の データフレームを作成します。
「df = pd.DataFrame(Lst)」の部分がデータフレーム作成コードです。
辞書型の Lst を与えてデータフレームを作成します。
### 20ページ データフレームの作成
# 各変数にリスト型を用いた。各変数をまとめるLstに辞書型を用いた
x = list(range(1, 4))
y = [160, 170, 180]
z = [50, 70, 80]
N = ['Kosugi', 'Shimizu', 'Kinosada']
Lst = dict(ID=x, height=y, weight=z, name=N)
df = pd.DataFrame(Lst)
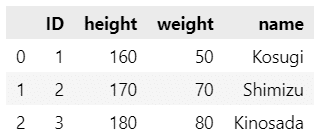
# データフレームの表示
df【実行結果】
numpy 配列 A を使ってデータフレームを作成します。
### 20ページ numpy配列からpandasデータフレームを作成
# as.data.frameに相当する関数がない。普通にデータフレームを作成する
# numpy配列ndarrayでAを構成
A = np.arange(1, 7).reshape((3, 2), order='F')
# データフレームに変換 列名は0から始まる整数値
dfA = pd.DataFrame(A)
dfA【実行結果】
列名が 0, 1 になっています。

列名を設定します。
### 21ページ 名前の変更
# 名前の変更
dfA.columns = ['VarName1', 'VarName2']
dfA【実行結果】

データフレームに対しても様々な演算を行えます。
平均値を計算してみましょう。
### 平均
dfA.mean(axis=0)【実行結果】
列単位の平均値を計算しました。


2.2.4 オブジェクトの型を確認する
テキストは R の lm 関数を用いて回帰分析を実行しています。
Python の回帰分析機能はさまざまな外部ライブラリで提供されています。
ここでは、R の lm 関数に近いアウトプットを出力できる statsmodels の ols (最小二乗法)を使います。
formula で回帰モデルを指定する場合には、「statsmodels.formula.api」を使用します。
statsmodelsを使うにはstatsmodelsをインポートする必要があります。
Python の慣例に従い、statsmodels.formula.api を smf と省略します。
### 21ページ 回帰分析 statsmodelsを利用
import statsmodels.formula.api as smf回帰分析を実行します。
最初のコードで回帰分析を実行して、結果を変数 result に入れています。
最後のコードで回帰係数を表示しています。
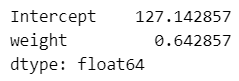
### 21ページ 回帰分析の実行、回帰係数の表示
result = smf.ols('height ~ weight', data=df).fit()
result.params【実行結果】
回帰分析の実行サマリーを表示します。
変数 result に対して .summary() を指定するとサマリーを見られます。
### 22ページ 回帰分析の結果表の表示
print(result.summary())【実行結果】
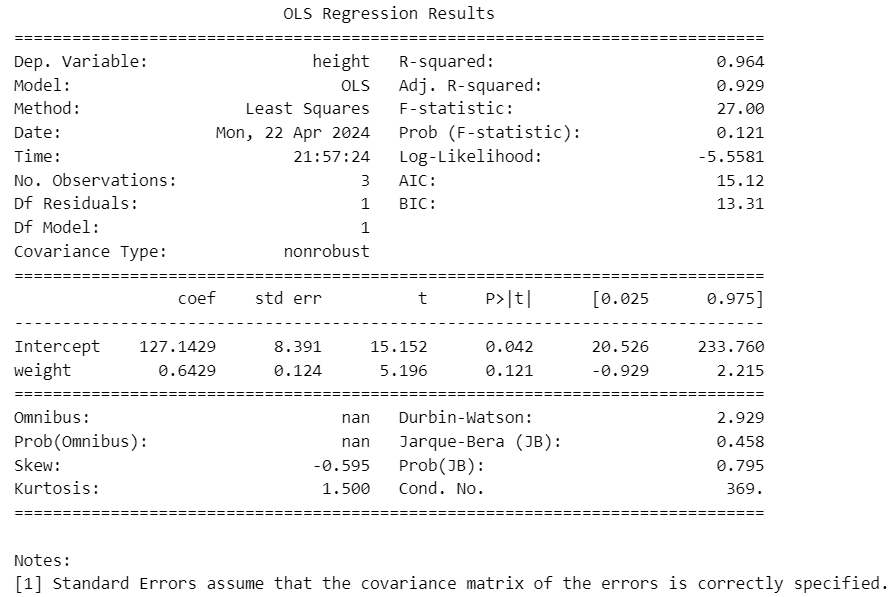
データフレーム df に含まれる変数の概要を見てみます。
R と完全一致しませんので、Python 特有処理と思っています。
### 23ページ データフレームの情報表示
# Rのstrに相当する汎用的な関数は不明
df.info()【実行結果】

テキスト23ページの回帰分析結果 result に対する構造表示については、Python Pandas には無さそうなので省略します。
テキスト23ページの回帰係数の表示は先程のコードと同じです。
### 25ページ 回帰係数の表示
result.params【実行結果】

回帰分析に投入した説明変数 height の値を取り出します。
### 25ページ 元データの取り出し
result.model.endog【実行結果】
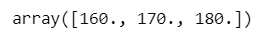
コラム「パイプ演算子」に関しては、Python にパイプ演算子に相当する処理が無さそうなので、省略いたします。
今回の写経は以上です。
変数と型は Python でも最重要テーマなので、ぜひぜひ身につけたいですね。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
