行列式 |A|=ad-bc の幾何学的意味

大学で「線形代数」を受講すると，いきなり行列式というのが登場する．２次正方行列 A の行列式は det(A) = ad-bc だと教わる．あるいは行列式を |A| と書くこともある．書き方はともかく，A の逆行列を求めるときに ad-bc が再登場するので，とりあえず覚える．でも，行列式って何だ？

今回は，行列式の幾何学的意味を簡単にまとめておこう．以前書いた記事「フーリエ級数展開は関数の座標を決めている」でも強調したように，数学の勉強をするとき，イメージを持って理解することはとても重要だ．

結論を述べると，２次正方行列の行列式は平行四辺形の面積である．

下図を見て欲しい．行列 A の１列目が橙色ベクトル，２列目が緑色ベクトルで，それらを２辺とする平行四辺形の面積が行列式 |A| だ．これは簡単に示すことができる．平行四辺形を含む長方形の面積から，平行四辺形の外側の面積を引けばいい．確かに，|A|= ad-bc が平行四辺形の面積だとわかる．

ちなみに，このスライドは明日の工学部新入生向けの講義「自然現象と数学」で使うので，スライド番号が書いてある．33枚目だ．

さて，これだけで「なるほど！」「おぉ〜凄い！」と感じてもらえたら嬉しいのだが，「で？」「だからどうした？」と思う人もいるだろう．「面積だとして，だから何なのか」と．

もう一歩，踏み込もう．

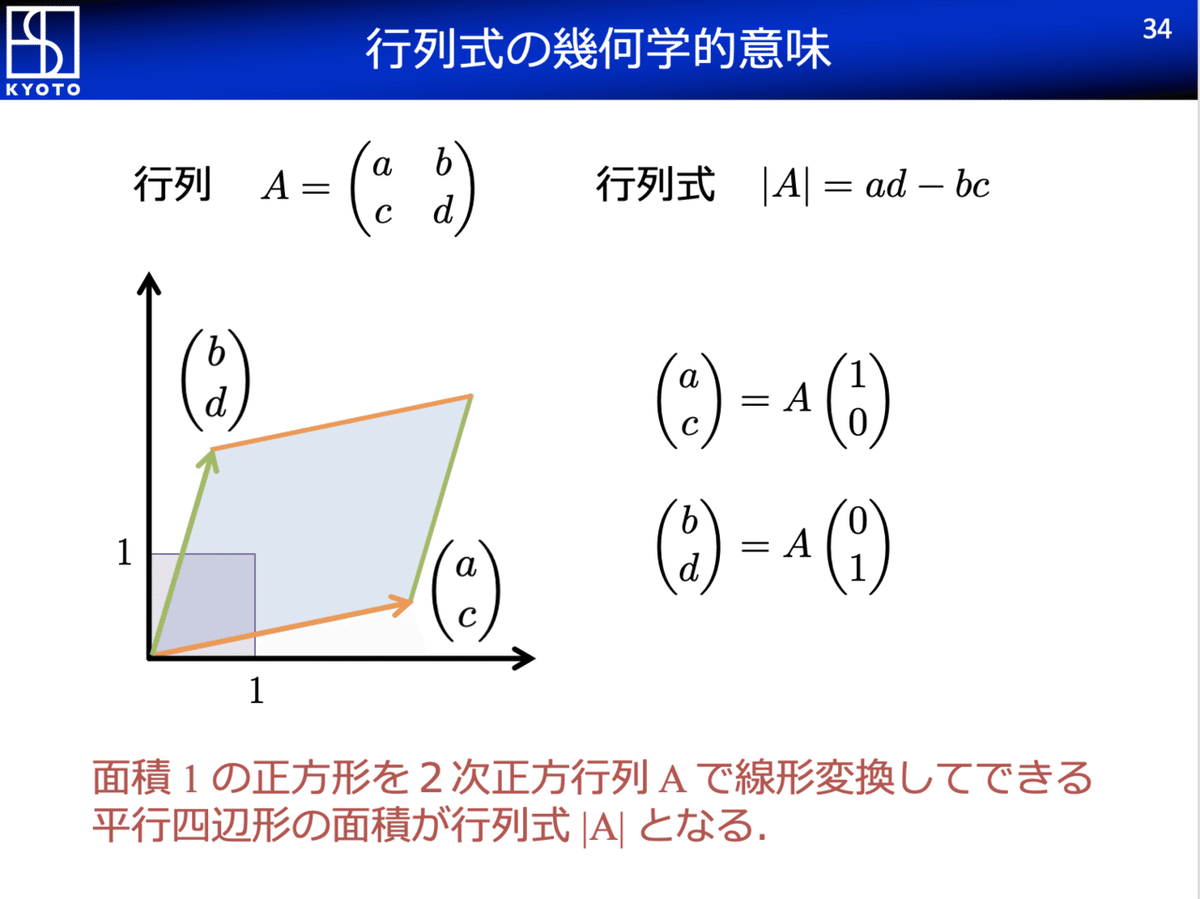
下図（34枚目のスライド）を見て欲しい．行列 A の１列目が橙色ベクトル，２列目が緑色ベクトルだったが，これらはそれぞれ，x 軸方向と y 軸方向の単位ベクトルを行列 A で線形変換してできるベクトルだ．つまり，各辺の長さが 1 の正方形（紫色）を平行四辺形（水色）に変形するのが，行列 A による線形変換ということになる．

このとき，元の正方形の面積は 1，変換後の平行四辺形の面積は |A| だ．つまり，行列式 |A| は，線形変換 A によって，正方形の面積が何倍になるかを意味している．

行列式が 0 になる，つまり |A| = 0 となるのは，どのようなときだろうか．そう，面積が 0 になるときだ．それは，橙色ベクトルと緑色ベクトルが一直線上になるときでもある．このとき，正方形は平行四辺形ではなく線分に変換され，面積は確かに 0 となる．

イメージを持つには，この２次元の説明で十分だと思うが，３次元でも同様のことが成り立つ．つまり，３次正方行列 B の３つの列ベクトルでつくられる平行６面体の体積が行列式 |B| に等しい．さらに，イメージは湧かないかもしれないが，４次元以上でも同様のことが成り立つ．

小さい行列が与えられたときに，手計算で行列式を計算できるのは，もちろん悪いことではない．計算できないよりも計算できた方がいい．ただ，ここで紹介したようなイメージを持たずに，サラスの公式だけ暗記して行列式が計算できたとしても，それこそ「で？」「だからどうした？」という感じになってしまう．繰り返すが，数学を勉強するときには，イメージを持とう．

© 2020 Manabu KANO.