
古代エジプトの数学書「リンド・パピルス」の問題を解く 〜リンド・パピルスの新解釈〜
「リンド・パピルス」79番目の問題
【完全数のお話】では、ネズミ算のお話をご紹介しましたが、古代エジプトにも似たようなお話があります。今回はリンド・パピルスと呼ばれる数学書に書かれている問題について考えましょう。リンド・パピルスは古代エジプトのアーメスという書記官が書いた数学書で、「アーメス•パピルス」と呼ばれることもあります。リンド・パピルスには数学の例題と解答が収められています。
その中の一問、79番目の問題には、次のような表だけが載っています。

スペルトとヘカトは小麦の量の単位で、スペルトは穂の本数を表し、1ヘカトは1枡を表します。古代には似たような問題が多いので、この問題の意味は復元することができます。数学史家は次のように復元しています。
あるところに7軒の家がありました。各々の家にはそれぞれ7匹の猫を飼っています。各々の猫は7匹のネズミを捕まえて食べます。各々のネズミは7穂の小麦(の種)を食べます。1穂の小麦からは7枡(ヘカト)の小麦が取れます。それでは、この7軒の家の猫はどれだけの小麦を救ったことになるでしょうか。

7軒の家にそれぞれ7匹の猫を飼っているので、猫は7 × 7= 49匹。各々の猫は7匹のネズミを捕まえて食べるので49 × 7= 343のネズミ・・・と計算していけば、全体でどれだけの小麦を救ったことになるかを計算することができそうです。
しかし、表1の右の表では、家の数、猫の数、ネズミの数、小麦の穂数、小麦の量を合計しています。家の数、猫の数、ネズミの数、小麦の量などなぜ足せないものを足しているのでしょうか。また、左の表の合計はなにを意味しているのでしょうか。
右の計算表は

を、左の計算表は

を表しています。19世紀のエジプト学の専門家アウグスト・アイゼンロールは、「エジプト数学は実用数学だとされてきたが、この問題は余暇に楽しむ娯楽問題だ」と述べています。娯楽のために足せないものを足したのでしょうか?この謎について考えてみましょう。
数列とは何か:数学用語の復習
数学史の専門家は「古代の数学は、古代の概念や古代の道具を用いて理解しなければならない」と注意しています。もちろんこれには十分留意しなければなりませんが、現代数学の概念を使って古代数学を見直すと、よりはっきりと理解できることが多いのです。今回は現代数学を利用して
古代数学を考えてみましょう。はじめに現代数学の用語を復習しておきましょう。
数をある規則に従って順番に並べたものを数列といいます。数列は数学の中でもっとも基本的で重要な概念です。もっとも基本的な数列は

で、これは自然数全部を小さい順に並べたものです。また、次の数列も古代の数学によく現れます。

1から始め、次々に2倍していく数列です。数列 (4) を、指数を使って表すと

となります。
一般に数列は、次のような添え字付きの変数の列で表わされます。

a₁ を第1項、a₂ を第2項 といい、n 番目の項 を第n項といいます。特に最初の a₁を初項といいます。

「数学は式が出てくるから嫌いだ」というのをよく耳にします。もちろん古代にはこのような記法はありません。人類が長い年月をかけてこのような記法を考えてきたのです。たとえば、数列 (4) を (5) のように書くと、意味がよりはっきりします。数列の第n項をnの式で表したもののことを一般項といいます。数列を表すには、具体的な数を並べて表さなくても、一般項を示しさえすればいいのです。たとえば (3) の数列の第n項は n で、(4) の数列の第 n 項は 2ⁿ⁻¹ です。
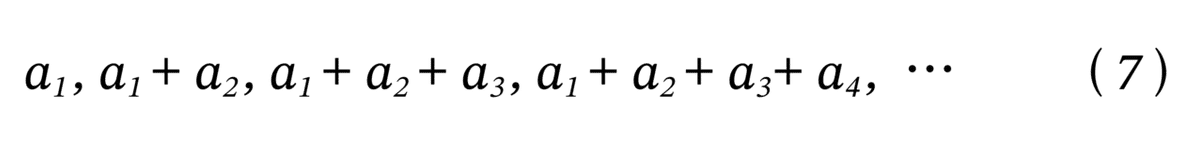
数列 (7) を数列 (6) の級数といいます。

リンド・パピルスの問題を数列で考える
さて、リンド・パピルスの問題に戻りましょう。表1の右に現れる数列は

です。この数列を a₁ , a₂ , …, a₅ とおきます。これをnの式で表すと

となります。数列 a₁, a₂ , … の級数を b₁, b₂, … とおきます。つまり、

です。
数列 a₁, a₂, … は、初項 7 から始め、毎回7倍すれば計算できます。この操作は、現在の数学を使って次のように式で表現できます。

同様にして、数列 b₁, b₂, … も次のようにして計算できます。

つまり

ここで、b₅ の計算に、最初に述べた表1の左側の計算 280+5602+11204 が現われていることに注目してください。2801 の7倍は、2801+2801×2+2801×4 と計算しています。古代エジプト人は、数列 a₁, a₂, … を計算する代わりに、数列 b₁, b₂, … を計算していたのです。

なぜ古代エジプト人は、直接「7ⁿ」を計算せず、級数(7ⁿの和)を計算したのでしょうか。その前に、この問題が書かれていたリンド・パピルスがどのようなものか調べてみましょう。
リンド・パピルスとは?
リンド・パピルスは、いまから3千700年ほど前に、アーメスという書記によって書かれた数学書です。アーメス自身はこの書を、さらに200年ほど前の古い書物からそのまま書き写したと述べています。

これまで、「エジプトやバビロニアなどオリエントの数学は、教えられた通り計算する方法を学ぶだけで、なぜそのようにするか、といった考察が少しもない」という“悪口”がよく言われてきました。おそらくこれは“ギリシア数学”との対比から言われたものと思われます。しかし、これは数学の内容の差というよりも、書かれた文書の性格の違いによるものではないかと思われます。たとえばユークリッドの『原論』は、最初の数巻は分かりやすいのですが、途中からとても難解で専門家でなければなかなか読みこなせるものではありません。これに対して、エジプトのリンド・パピルスは、書記学校の生徒の教育用の資料です。例えていうと、現在の高校とか中学校の“受験参考書”です。
上の問題を書き写したアーメスは、理解できない部分を書き写さなかったかもしれません。「小麦(スペルト) 2401」は、実際のパピルスでは「2301」となっていますが、これは明らかに写し間違いです。おそらくアーメスは、与えられた数 r と n に対して、rⁿの計算方法ではなく、

の計算方法だけを知っていたのではないかと思われます。よく受験生に、ある問題の解き方を教えて、別の解き方の説明をしようとすると、「解き方は1つで十分です」と答えが返ってくるといいます。古代エジプト人も、自分達が使いやすい計算方法を習得し、その一つの計算方法をいろいろな場面で使っていたのかもしれません。
エジプト人は等比級数の公式を知っていた!
「数列 aₙ を計算する代わりにその級数 bₙ を計算した」というのは単なる想像で、確たる証拠があるわけではありません。しかし、少なくとも次のことは言えます。表1の右側は (1) で示されるように、等比数列 7, 72, … の第5項までの和であり、表1 の左側はこの数列の第4項までの和 2800 に1を加えたものの7倍です。表1は両者が等しいことをいっています。つまり、上の記号を使えば、

が成立することをエジプト人は理解していたと思います。つまりエジプト人は、この問題で足せないものを足す数学的ゲームそしているわけではなく、等比数列には表1で示されるような不思議な性質があることを示したかったのだと思います。足せないものを足すという数学の持つ自由さをエジプト人はすでに体得していたのだと思います。
![]()
▼数学Webマガジン・マテマティカ 『ピラミッドの謎』
エジプトのピラミッドには多くの謎が隠されています。マテマティカのWeb連載『ピラミッドの謎』では、ピラミッドの数に関する3つの謎「円周率の謎」「黄金比の謎」「地球の緯度の謎」を取り上げます。エジプト文明が栄えた時代の人々の暮らしやエジプト神話、そして古代エジプトの数学能力など、様々な角度からピラミッドの謎に迫ります!
▼数学Webマガジン・マテマティカ 『バビロニアの数』
皆さんは、むかし南メソポタミア地方に栄えたバビロニアという国をご存知でしょうか。最近になって太古の昔この地に高度な数学や天文学が発展していることが分かってきました。マテマティカWeb連載『 バビロニアの数 』では、60進数という記数法はどのようにして生まれたのか、バビロニアで行われていた高度な計算とはどのようなものだったのか、などバビロニア数学に焦点を当て詳しく紹介しています。ぜひご訪問ください!
![]()
▼ Twitter、Webマガジンサイトも更新中。よろしくお願いいたします。
Twitter: @mathematicasite
Web:http://mathematica.site/
この記事が気に入ったらサポートをしてみませんか?


