
Processing でグラフを描く⑯ ハーモノグラフ
Processing でグラフを描く 第16回目です。
ハーモノグラフは振り子を使って幾何学的な模様を生成する機械です。縦横2重の振り子を用いることで、複雑な模様をジェネラティブに作成できます。19世紀に発明されましたが、ジェネラティブアートの元祖かもしれません。作画するには大掛かりな装置が必要ですが、現在ではコンピュータで簡単に再現できます。Processing を使って、ハーモノグラフを描いてみましょう。
ハーモノグラフの定義式
$$
x = a_1 sin(f_1 t + p_1) e^{- d_1 t} + a_2 sin(f_2 t + p_2) e^{- d_2 t}\\
y = a_3 sin(f_3 t + p_3) e^{- d_3 t} + a_4 sin(f_4 t + p_4) e^{- d_4 t}
$$
上記の式がハーモノグラフの定義式です。媒介変数 t で表されるx, y を平面上にプロットすると、複雑な曲線が現れます。係数がたくさんあるので複雑に見えますが、振り子が2つ縦横に動いていることをイメージしてください。振り子は正弦関数(sine)で近似できるのでしたね。$${a_1, a_2, a_3, a_4}$$ は振り子の振幅を表します。$${f_1, f_2, f_3, f_4}$$ は振り子の周波数を表します。$${p_1, p_2, p_3, p_4}$$ は振り子の位相のずれを表します。これらの係数を適切に設定することで面白いグラフを描くことができます。
そして最後、$${d_1, d_2, d_3, d_4}$$ は振り子の減衰率を表します。現実のハーモノグラフはペンなどで紙に書いて作画するので、振り子の振幅が少しずつ小さくなっていきます。それを再現するのが減衰率です。
ハーモノグラフをコード化する
def harmono_graph(t, a, f, p, d):
x = a[0] * sin(f[0] * t + p[0]) * exp(-d[0] * t) + a[1] * sin(f[1] * t + p[1]) * exp(-d[1] * t)
y = a[2] * sin(f[2] * t + p[2]) * exp(-d[2] * t) + a[3] * sin(f[3] * t + p[3]) * exp(-d[3] * t)
return x, yハーモノグラフの定義式を pythonで再現すると、上記のコードになります。関数hamono_graph は5つの引数を持ち、それぞれ時間(t)、振幅(a)、周波数(f)、位相のずれ(p)、減衰率(d)を表しています。
次に、実際にハーモノグラフを描いてみます。
初めてのハーモノグラフ
SIZE = 1000 # 画面サイズ
RADIUS = 150
points_list = []
def setup():
global tex
size(SIZE, SIZE)
frameRate(6)
# グラフのデータ
for i in range(101):
a = [RADIUS, RADIUS, RADIUS, RADIUS]
f = [
1 + i * 0.01,
1,
1,
1,
]
p = [
0,
0,
HALF_PI,
HALF_PI,
]
d = [
.001,
.001,
.001,
.001,
]
points = [a, f, p, d]
for t in range(5000):
points.append(harmono_graph(t * 0.1, a, f, p, d))
points_list.append(points)
def draw():
background(127)
pushMatrix()
translate(width / 2, height / 2)
count = min(frameCount - 1, len(points_list) - 1)
points = points_list[count][4:]
for i in range(len(points) - 1):
x1 = points[i][0]
y1 = points[i][1]
x2 = points[i + 1][0]
y2 = points[i + 1][1]
line(x1, y1, x2, y2)
popMatrix()
def harmono_graph(t, a, f, p, d):
x = a[0] * sin(f[0] * t + p[0]) * exp(-d[0] * t) + a[1] * sin(f[1] * t + p[1]) * exp(-d[1] * t)
y = a[2] * sin(f[2] * t + p[2]) * exp(-d[2] * t) + a[3] * sin(f[3] * t + p[3]) * exp(-d[3] * t)
return x, y
今回の課題は、適切な係数を見つけて面白い図形をたくさん描くことです。振幅は図形の最大サイズに関係しているので、振り子の振幅 $${a_1, a_2, a_3, a_4}$$ はすべて同じ値にします。画面サイズ(1000)に対して、15%程度がちょうどよい大きさで描画できます。減衰率は大きすぎるとすぐに振幅が小さくなり、小さすぎると変化が見えません。何度か試してみましたが、今回はd = 0.001 に設定することにします。(お好みで減衰率は変更してください。)
そうすると、動かす係数が周波数 $${f_1, f_2, f_3, f_4}$$ 、位相のずれ $${p_1, p_2, p_3, p_4}$$ の8個に絞られます。試しに $${f_1}$$ のみ 0.01刻みで動かして101枚の画像を作成しました。8つの係数のうち1つ動かすだけで面白いグラフが描けます。他の係数も動かしてみましょう。
周波数を変更してみる
f = [
1.01,
1 + i * 0.05,
1,
1,
]
周波数を変更したときの画像の変化を見てみます。$${f_1 = 0.01}$$ に固定して、$${f_2}$$ のみを 0.05刻みで増やしていきます。 周波数が 0.5 の倍数のとき、適度にまとまったグラフが現れるようですね。
f = [
1.01,
1 + i * 0.05,
1 + i * 0.05,
1,
]
$${f_1 = 1.01}$$ に固定して、$${f_2, f_3}$$ を 0.05刻みで増やしていきます。先ほどと同じように 0.5の倍数のとき面白いグラフが現れました。 大円の中に4つの小円が含まれているのが観察できました。
f = [
1.01,
1 + i * 0.05,
1 + i * 0.1,
1,
]
$${f_1 = 1.01}$$ に固定して、$${f_2}$$ を 0.05刻みで、$${f_2}$$ を 0.1刻みで増やしていきます。 かなり複雑な形になってきました。周波数を上げすぎると、プロットの移動が大きくなりすぎて、線がギザギザになってしまいます。
f = [
1.01,
int(random(10)) / 2.0,
int(random(10)) / 2.0 + 0.01,
int(random(10)) / 2.0,
]
$${f_1 = 1.01}$$ に固定して、$${f_2, f_3, f_4}$$ を 0.5刻みでランダムに変化させてみました。乱雑さを増やすため、$${f_3}$$ は 0.01 を加えています。周波数を変化させるだけで、これほど多彩なグラフが描けるのです。
次に、位相のずれがグラフにどのように作用するか検証してみます。
位相のずれを変更してみる
f = [
1.01,
1,
1,
1,
]
p = [
0 + i * TWO_PI / 100,
0,
HALF_PI,
HALF_PI,
]
$${f_1 = 1.01}$$ に固定して、$${p_1}$$ を 3.6° ずつ変更(100回で一周)したときのグラフです。ねじれたパイプのようなグラフが描かれました。
f = [
1.01,
1,
1,
1,
]
p = [
0,
0 + i * TWO_PI / 100,
HALF_PI + i * TWO_PI / 100,
HALF_PI,
]
$${f_1 = 1.01}$$ に固定して、$${p_2, p_3}$$ を 3.6° ずつ変更(100回で一周)したときのグラフです。$${p_2, p_3}$$ を同じように動かすと、グラフが収束して小さくなってしまいました。位相のずれは同じように動かさない方がよさそうです。今度はバラバラ(ランダム)に変化させてみましょう。
f = [
1.01,
1,
1,
1,
]
p = [
0,
random(TWO_PI),
random(TWO_PI),
random(TWO_PI),
]
$${f_1 = 1.01}$$ に固定して、$${p_2, p_3, p_4}$$ を360度の範囲でランダムに動かしてみました。位相が打ち消しあうことでグラフが大きくなったり小さくなったりすることが観察できました。
周波数と位相のずれがグラフにどのような影響を与えるか、観察してきました。最後に、ハーモノグラフのアニメーションを作って遊びましょう。
ハーモノグラフのアニメーション
SIZE = 1000 # 画面サイズ
RADIUS = 150
points_list = []
t = 0
a, f, p, d = None, None, None, None
def setup():
global tex
size(SIZE, SIZE)
frameRate(60)
colorMode(HSB, 360, 100, 100)
background(0)
# 係数を設定
set_coefficient()
def draw():
global t
translate(width / 2, height / 2)
for i in range(1000):
stroke(t % 360, 100, 100)
x, y = harmono_graph(t)
point(x, y)
t += 0.001
def set_coefficient():
global t, a, f, p, d
t = 0
a = [RADIUS, RADIUS, RADIUS, RADIUS]
f = [
1.01,
int(random(10)) / 2.0,
int(random(10)) / 2.0 + 0.01,
int(random(10)) / 2.0,
]
p = [
0,
random(TWO_PI),
random(TWO_PI),
random(TWO_PI),
]
d = [
.001,
.001,
.001,
.001,
]
def harmono_graph(t):
x = a[0] * sin(f[0] * t + p[0]) * exp(-d[0] * t) + a[1] * sin(f[1] * t + p[1]) * exp(-d[1] * t)
y = a[2] * sin(f[2] * t + p[2]) * exp(-d[2] * t) + a[3] * sin(f[3] * t + p[3]) * exp(-d[3] * t)
return x, y
def mousePressed():
background(0)
set_coefficient()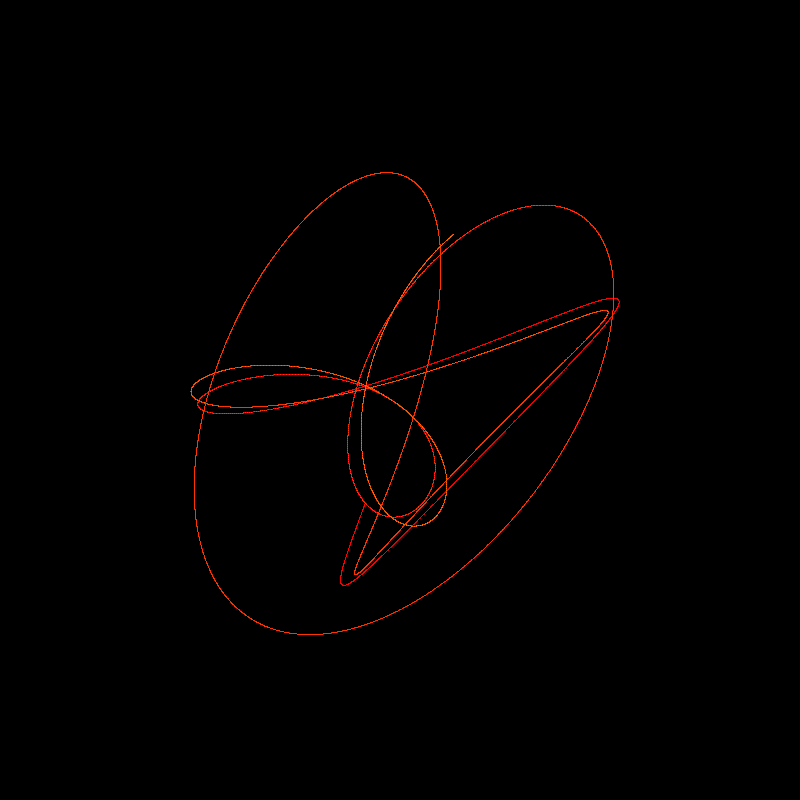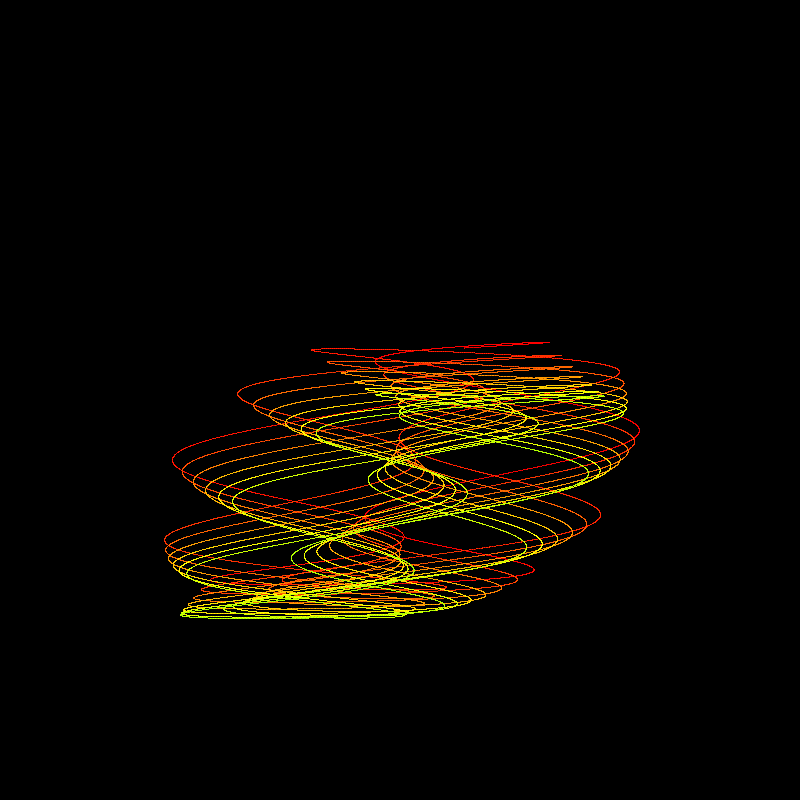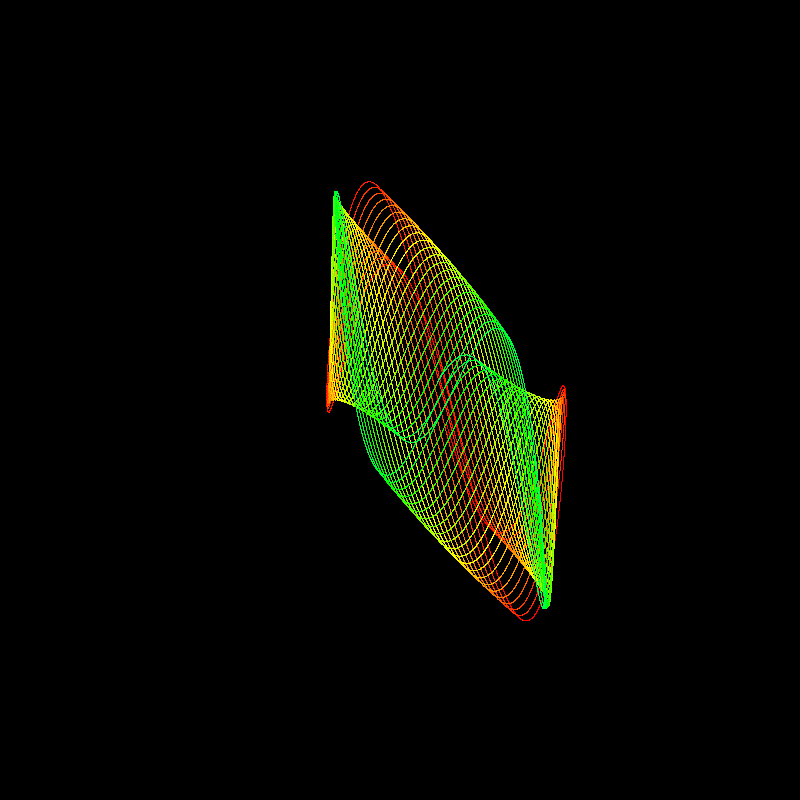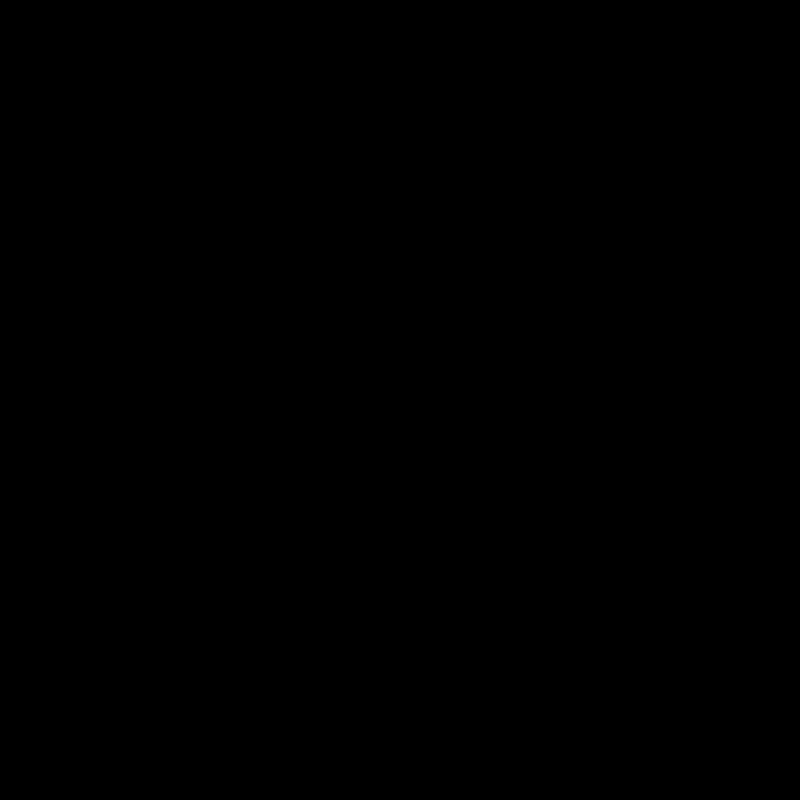
やはりハーモノグラフはアニメーションにする方が面白いですね。前の節で見つけた周波数と位相のずれをそのまま採用してみましたが、ハーモノグラフっぽくなったと思います。colorMode を HSB に変更し、変数t によって段階的に色が変わるようにしました。画面上でマウスをクリックすると、別のハーモノグラフが描かれるように実装しました。
note に投稿するためにフレームが飛んでいますが、実際にはもっとスムーズに動きますので、ぜひ自分のパソコンで動かしてみてください。係数を設定するための関数set_coefficient を改造すれば、もっと面白い画像が現れるかもしれません。挑戦してみてください。
面白い画像が出来たら、note に投稿してみてくださいねー 待ってます!
前の記事
Processing でグラフを描く⑮ ストレンジアトラクターのアニメーション
次の記事
Processing でグラフを描く⑰ らせん
その他のタイトルはこちら
この記事が気に入ったらサポートをしてみませんか?
