
Processing でグラフを描く⑨ マンデルブロ集合
Processing でグラフを描く 第9回目です。
マンデルブロ集合に初めて出会ったのはいつだったでしょうか。一目惚れでした。うまく説明できないので「一目惚れ」としか表現できないですが、なにか深遠に触れたような感覚がずっと残っているのです。
マンデルブロ集合をスマホやパソコンの待ち受け画面にしてますが、嫁に「なにそれ、気持ち悪い。」と言われてしまいました。人によっては気持ち悪いと感じるみたいですね。皆様はトップの画像を見て、どう思われましたか? 自分で描いてみたいと思いませんか?
まずは作画の準備をいたしましょう。複素数について考えていきます。
すべてのコードを公開したので、コピペで実行可能です。Processing3 の pythonモードに貼り付けて実行してください。
複素数

普通に使っている数字を実数といいます。りんごが5個とか体重が100キロとか日常生活で使っている概念です。
複素数は実数を数学上で拡張したものと考えることができます。二乗すると -1 になる数を虚数単位 i と定義して、複素数は $${z = a + bi (a,b は実数)}$$ と定義されます。b = 0 のとき、z は実数となるため、複素数は実数を含みます。
複素数は実数と同じように算術計算することができます。足し算、掛け算、その大きさの計算を次に見ていきましょう。
複素数の加算、乗算、大きさ

$$
z_1 = a + bi\\
z_2 = c + di\\
z_1 + z_2 = (a + c) + (b + d)i
$$
複素数の足し算は直感的に理解できます。実数部同士、虚数部同士を加えるだけです。図から明らかなように、どちらから足しても同じ答えが得られます。

$$
z_1 = a + bi\\
z_2 = c + di\\
z_1 \times z2 = (a + bi) \times (c + di)\\
= ac + adi + bdi - bd\\
= (ac - bd) + (ad + bc)i
$$
複素数の掛け算については、直感的に捉えるのは難しいかと思います。虚数部同士の掛け算は $${i^2 = -1}$$ より $${-bd}$$ になることに注意が必要です。足し算と同じように、どちらから掛けても同じ答えになります。
複素数の大きさは原点からの距離と考えることができます。複素数 $${z = a + bi}$$ の大きさは $${\sqrt{a^2 + b^2}}$$ と定義できます。
マンデルブロ集合
$$
\begin{equation*}
\left\{ \,
\begin{aligned}
& z_{n+1} = z_n^2 + c \\
& z_0 = 0 \\
\end{aligned}
\right.
\end{equation*}
$$
マンデルブロ集合の定義式です。平面上のすべての点 c に対して、定義式を当てはめて、$${n \rightarrow \infin}$$ の極限で、その大きさが発散しない($${\infin}$$ にならない)点の集合を求めます。その結果がトップ画像になるのです。そのことを Processing で検証します。
マンデルブロ集合を描く
SIZE = 1000 # 画像サイズ
RANGE = [ # 作画範囲
[-2, 2],
[-2, 2]
]
max_num = 100 # 繰り返し回数
colors_list = []
def setup():
size(SIZE, SIZE)
# size(SIZE * 6, SIZE * 6)
background(255)
noStroke()
colorMode(HSB, 100)
noLoop()
# グラフのデータ
colors_list.append(mandelbrot())
def draw():
# グラフを描く
colors = colors_list[0]
screen_size = int(sqrt(len(colors)))
for j in range(screen_size):
for i in range(screen_size):
col = colors[j * screen_size + i]
if col == max_num:
# 発散しないとき
fill(0)
else:
# 発散するとき、回数によって色を分ける
fill(col * 3, 100, 100)
rect(i, j, 1, 1)
# 複素数の足し算
def complex_add(a, b):
return [a[0] + b[0], a[1] + b[1]]
# 複素数の掛け算
def complex_mult(a, b):
return [
a[0] * b[0] - a[1] * b[1],
a[0] * b[1] + a[1] * b[0]
]
# 複素数の大きさ
def complex_magnitude(a):
return sqrt(a[0] ** 2 + a[1] ** 2)
# マンデルブロ集合
def mandelbrot(z0=(0, 0), screen_size=SIZE, screen_range=RANGE):
x_scale = (screen_range[0][1] - screen_range[0][0]) / float(screen_size)
y_scale = (screen_range[1][1] - screen_range[1][0]) / float(screen_size)
colors = []
for j in range(screen_size):
for i in range(screen_size):
# 平面上の点を取る
c = [
screen_range[0][0] + i * x_scale,
screen_range[1][0] + j * y_scale
]
# z1 を求める
z = complex_add(complex_mult(z0, z0), c)
for k in range(max_num):
if complex_magnitude(z) > 2.0:
# 発散したら break
colors.append(k)
break
z = complex_add(complex_mult(z, z), c)
else:
# 発散しなかったとき
colors.append(max_num)
# 発散までの回数(描画の時に色に変換)のリストを返す
return colors
上記のコードを実行すると、マンデルブロ集合が現れました。計算量が大きいので時間がかかるかもしれません。そのときは自分の環境に合わせて、SIZE の値を小さくしてください。SIZE = 200 くらいにすると比較的早く計算が終わるはずです。
コードにコメントを入れておいたので、興味のある方は見てください。複素数の計算をする関数(complex_xxx)とマンデルブロ集合を計算する関数(mandelbrot)を含んでいます。前の節で説明したことが、Python のプログラムとして記述してありますから、見比べて確認してみてください。
背景のグラデーションですが、一番外の赤色が0回目で発散している範囲です。今回は発散の条件を「複素数の大きさが 2 以上」として計算したので、半径 2 より大きい部分が発散しています。その内側が発散の回数が 1回、2回、3回…の範囲を色分けしています。色が赤から紫に行くに従って、発散しにくくなると理解できます。
マンデルブロ集合の微細構造を見る
# 作画範囲を変更
# RANGE = [
# [-2, 2],
# [-2, 2]
# ]
RANGE = [
[-0.5, 0.5],
[-1.5, -0.5]
]
描画する範囲を変更するだけで、マンデルブロ集合の微細構造を確認できます。部分の中に全体を含むフラクタル構造が現れています。ここがマンデルブロ集合の最大の特徴かと思います。
YouTube などで見たことがあるかもしれませんが、どこまで拡大してもマンデルブロ集合の形が現れます。この簡単なプログラムからも、フラクタル構造が確認できました。
アニメーション(解像度)
SIZE = 1024
RANGE = [
[-2, 2],
[-2, 2]
]
max_num = 100
colors_list = []
tex = None
image_name = '_sample'
def setup():
global tex
size(SIZE, SIZE)
# size(SIZE * 6, SIZE * 6)
background(255)
noStroke()
colorMode(HSB, 100)
frameRate(1)
# グラフのデータ
for i in range(10):
colors_list.append(mandelbrot(screen_size=2**i))
def draw():
# グラフを描く
count = min(frameCount - 1, len(colors_list) - 1)
colors = colors_list[count]
screen_size = int(sqrt(len(colors)))
pixel_size = SIZE / screen_size
for j in range(screen_size):
for i in range(screen_size):
col = colors[j * screen_size + i]
if col == max_num:
# 発散しないとき
fill(0)
else:
# 発散するとき、回数によって色を分ける
fill(col * 3, 100, 100)
rect(
i * pixel_size,
j * pixel_size,
pixel_size,
pixel_size
)
# 複素数の足し算
def complex_add(a, b):
return [a[0] + b[0], a[1] + b[1]]
# 複素数の掛け算
def complex_mult(a, b):
return [
a[0] * b[0] - a[1] * b[1],
a[0] * b[1] + a[1] * b[0]
]
# 複素数の大きさ
def complex_magnitude(a):
return sqrt(a[0] ** 2 + a[1] ** 2)
# マンデルブロ集合
def mandelbrot(z0=(0, 0), screen_size=SIZE, screen_range=RANGE):
x_scale = (screen_range[0][1] - screen_range[0][0]) / float(screen_size)
y_scale = (screen_range[1][1] - screen_range[1][0]) / float(screen_size)
colors = []
for j in range(screen_size):
for i in range(screen_size):
# 平面上の点を取る
c = [
screen_range[0][0] + i * x_scale,
screen_range[1][0] + j * y_scale
]
# z1 を求める
z = complex_add(complex_mult(z0, z0), c)
for k in range(max_num):
if complex_magnitude(z) > 2.0:
# 発散したら break
colors.append(k)
break
z = complex_add(complex_mult(z, z), c)
else:
# 発散しなかったとき
colors.append(max_num)
# 発散までの回数(描画の時に色に変換)のリストを返す
return colors
作画範囲 $${-2 < x <2, -2 < y < 2}$$ の解像度を変化させたときのアニメーションです。解像度 $${2^0, 2^1, 2^2… 2^{10}}$$ の順で作画しています。
手計算でマンデルブロ集合を描いた数学者がいたと、何かで読みました。どの解像度で計算したのか興味ありますね。$${256 \times 256}$$ の画像を作成するためには、$${65,536}$$ 回も計算しなければなりません。半径2以上はすぐに発散するので省くとしても、大変な労力が必要になります。
アニメーション(拡大)
# グラフのデータ
for i in range(11):
zoom = sqrt(3.0 / 2)**i
zoom_center = [-sqrt(2), 0]
w, h = 1.0 / (2**zoom), 1.0 / (2**zoom)
zoom_range = [
[zoom_center[0] - w / 2, zoom_center[0] + w / 2],
[zoom_center[1] - h / 2, zoom_center[1] + h / 2]
]
colors_list.append(mandelbrot(screen_range=zoom_range))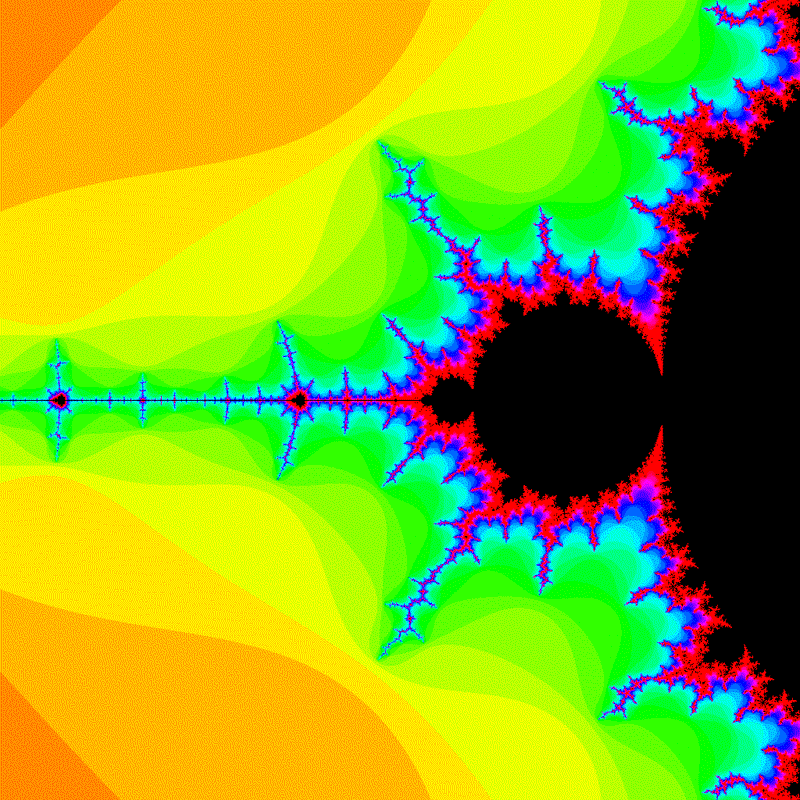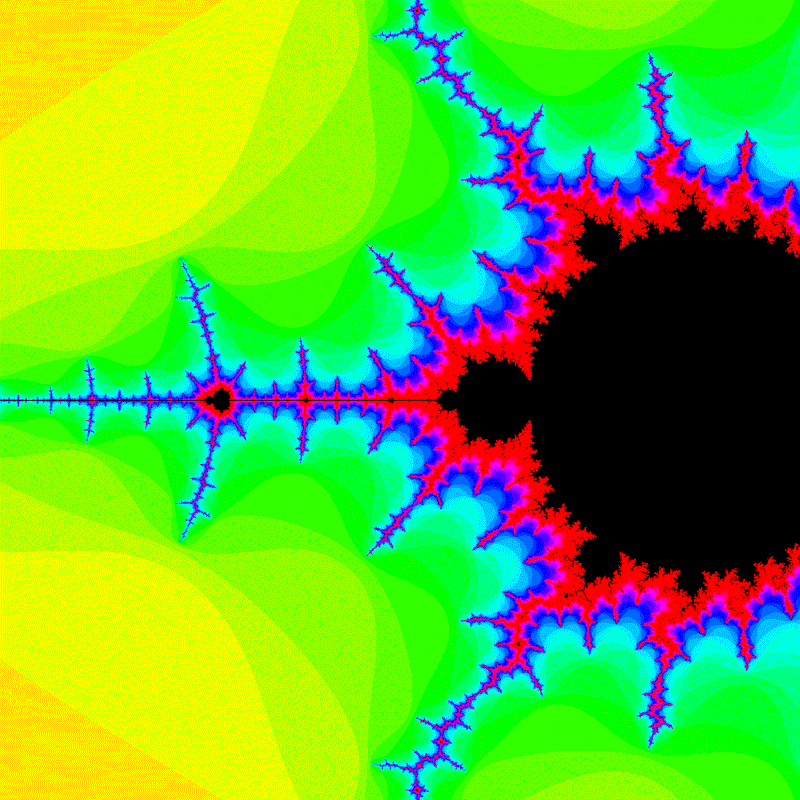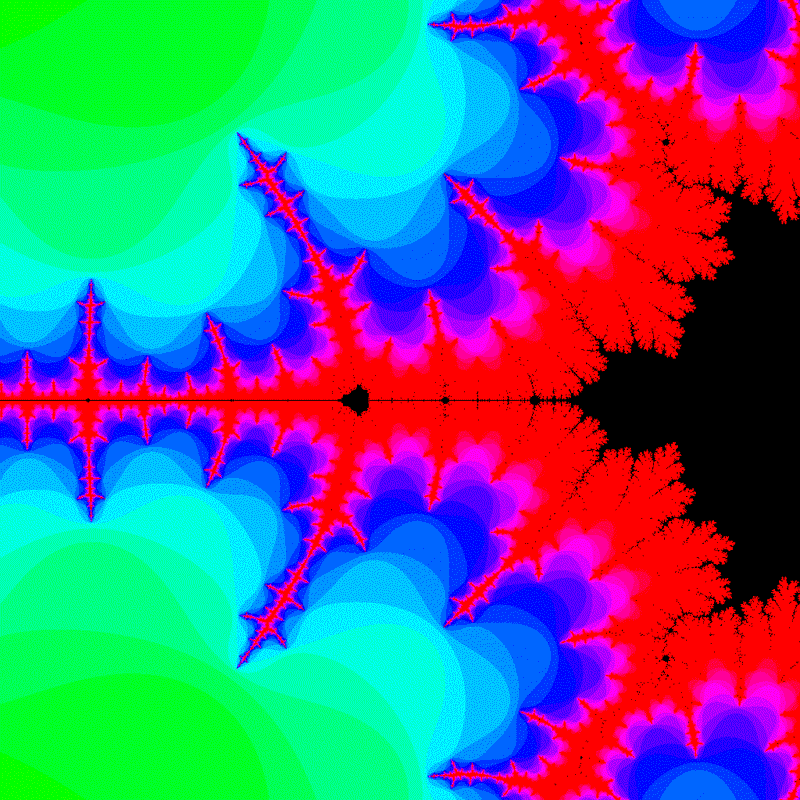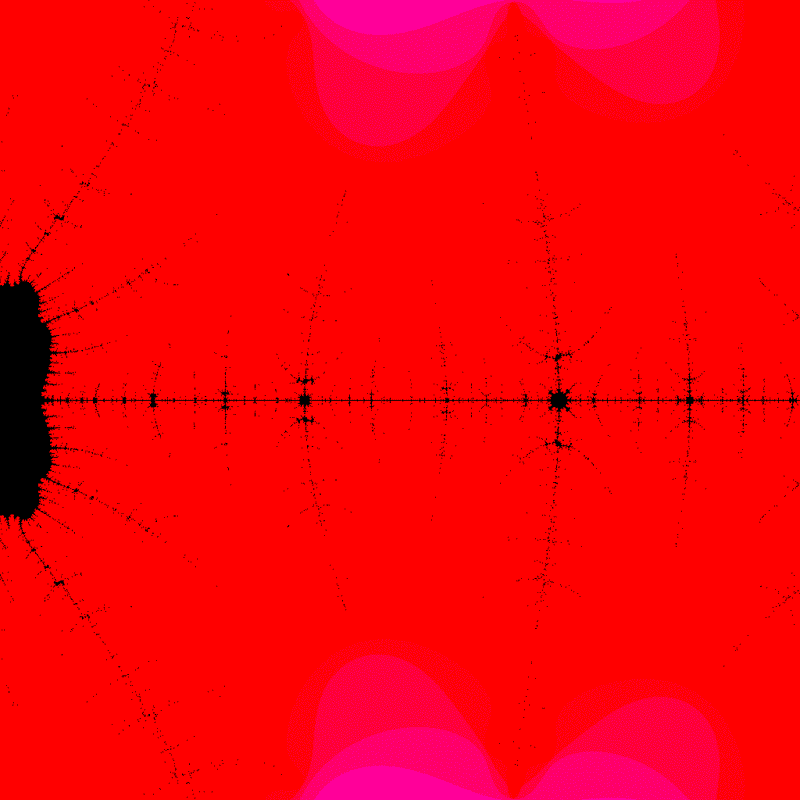
YouTubeでおなじみのマンデルブロ集合の拡大動画です。グラフのデータ作成部分の変数zoom_center で拡大する中心を指定します。パソコンの性能が許すなら繰り返し回数を増やしてさらに拡大することが可能です。
初期値 z0 を変更してみる
SIZE = 1200
SUB_SIZE = int(SIZE / 6)
RANGE = [
[-2, 2],
[-2, 2]
]
max_num = 100
colors_list = []
def setup():
size(SIZE, SIZE)
# size(SIZE * 6, SIZE * 6)
background(255)
noStroke()
colorMode(HSB, 100)
noLoop()
# グラフのデータ
for i in range(36):
z0 = [cos(radians(i * 10)), sin(radians(i * 10))]
colors_list.append(mandelbrot(z0=z0, screen_size=SUB_SIZE))
def draw():
# グラフを描く
for k in range(len(colors_list)):
noStroke()
colors = colors_list[k]
screen_size = int(sqrt(len(colors)))
row_num = k % 6
column_num = int(k / 6)
sub_x_scale = (RANGE[0][1] - RANGE[0][0]) / float(SUB_SIZE)
sub_y_scale = (RANGE[1][1] - RANGE[1][0]) / float(SUB_SIZE)
for j in range(screen_size):
for i in range(screen_size):
col = colors[j * screen_size + i]
x = row_num * SUB_SIZE + i
y = column_num * SUB_SIZE + j
if col == max_num:
# 発散しないとき
fill(0)
else:
# 発散するとき、回数によって色を分ける
fill(col * 3, 100, 100)
rect(x, y, 1, 1)
else:
fill(0)
pushMatrix()
translate(row_num * SUB_SIZE, column_num * SUB_SIZE)
z0 = [round(cos(radians(k * 10)), 3), round(sin(radians(k * 10)), 3)]
text(
'z0 = ' + str(z0[0]) + '+' + str(z0[1]) + 'i',
10,
15
)
stroke(0)
pushMatrix()
translate(SUB_SIZE / 2, SUB_SIZE / 2)
ellipse(z0[0] / sub_x_scale, -z0[1] / sub_y_scale, 5, 5)
line(
z0[0] / sub_x_scale,
-SUB_SIZE / 2,
z0[0] / sub_x_scale,
SUB_SIZE / 2
)
line(
-SUB_SIZE / 2,
-z0[1] / sub_y_scale,
SUB_SIZE / 2,
-z0[1] / sub_y_scale
)
popMatrix()
popMatrix()
# 複素数の足し算
def complex_add(a, b):
return [a[0] + b[0], a[1] + b[1]]
# 複素数の掛け算
def complex_mult(a, b):
return [
a[0] * b[0] - a[1] * b[1],
a[0] * b[1] + a[1] * b[0]
]
# 複素数の大きさ
def complex_magnitude(a):
return sqrt(a[0] ** 2 + a[1] ** 2)
# マンデルブロ集合
def mandelbrot(z0=(0, 0), screen_size=SIZE, screen_range=RANGE):
x_scale = (screen_range[0][1] - screen_range[0][0]) / float(screen_size)
y_scale = (screen_range[1][1] - screen_range[1][0]) / float(screen_size)
colors = []
for j in range(screen_size):
for i in range(screen_size):
# 平面上の点を取る
c = [
screen_range[0][0] + i * x_scale,
screen_range[1][0] + j * y_scale
]
# z1 を求める
z = complex_add(complex_mult(z0, z0), c)
for k in range(max_num):
if complex_magnitude(z) > 2.0:
# 発散したら break
colors.append(k)
break
z = complex_add(complex_mult(z, z), c)
else:
# 発散しなかったとき
colors.append(max_num)
# 発散までの回数(描画の時に色に変換)のリストを返す
return colors
マンデルブロ集合の定義式 $${z_{n+1} = z_n^2 + c, z_0 = 0}$$ において、初期値 $${z_0}$$ を変化させたときどのような図形が現れるのか。そのことは長年の疑問でしたが、今回コンピューターの力を借りて(computer oriented)作画してみました。36枚の図を並べて、初期値 $${z_0}$$ の位置を線で示しました。
$${z_0}$$ は半径 1 の円周上を36等分した点に設定しました。上記コードの「グラフのデータ」を作成している部分をご確認ください。この部分を修正すると、任意の点を指定できます。
$${z_0 = 1, z_0 = -1}$$ は同型、$${z_0 = i, z_0 = -i}$$ も同型であることが見て取れます。あの有名な「お尻」が観察できなくなるのは残念です(笑)。アニメーションにせず、静止画を並べることで、$${z_0}$$ の変化をより捉えられやすくなることがわかりました。($${z_0}$$ で面白い図形が現れる特異点があれば、コメントで教えてくださいね。)
発展的課題 ジュリア集合

あー面白い、マンデルブロは面白すぎる。自分のパソコンで作画できるようになり、「マンデルブロ愛」がより深まったように思います。親戚の「ジュリア集合」という図形があり、今回のコードを少し修正するだけで作画可能です。読者諸氏の挑戦を期待しています。
前の記事
Processing でグラフを描く⑧ スピログラフ
次の記事
Processing でグラフを描く⑩ 3次元のグラフ
その他のタイトルはこちら
この記事が気に入ったらサポートをしてみませんか?
