
【ベクトル】 〈5〉 減法がMethod
ベクトルは、小学校からずっと習ってきた「数」とは、ちょっと異なる量です。方向が加わっているのが理由ですが、そのおかげで「図形」にも応用しやすく大変便利な道具です。
「数」+「図形」、つまり、長さや成分のような数量=代数的な意味合いと、方向を持った矢印=幾何的な意味合いが含まれているのがベクトルです。「方程式」の解説でも述べましたが、数学の面白さ、美しさを味わうことのできる分野ですので、順に、整理していきましょう。
[Method] 減法を最大限活用
「減法」をうまく使いこなせるかどうかでベクトルを克服できるかどうかが決まる!
① 和からの変形
② 反対ベクトル
③ 終点と終点をつないだベクトル
④ 成分で表されたベクトル(平面)(空間)
⑤ 位置ベクトル
上記のうち、③を中心にマスターし、どの場合にどれを使っていくのかを見極めていきたいですね。④⑤は、③の派生なので。
① 和からの変形(ベクトルの結合)
基本は、OからAを経由してBに辿り着くと考えると、
(OA→)+(AB→)=OB→
より、代数的に考えて、
AB→=(OB→)ー(OA→)
が導かれる。
ただ、証明的に使われることはあっても、頻度は少ない。

② 反対ベクトル
ベクトルらしく、幾何的に考えて、逆方向に辿るようにして、AからOを経由してBに辿り着くと考えると、
AB→=ー(AO→)+(OB→)
より、
AB→=(OB→)ー(OA→)
が導かれる。

③ 終点と終点をつないだベクトル
①②の結果からわかるように、
AB→は、Oから終点B、終点Aへのベクトルの引き算となる。これを、
AB→は、「先から根元を引く」
と言うこととする。
このとき、始点はOでなくても、どの点であっても良い。
AB→=(OB→)ー(OA→)
=(CB→)ー(CA→)
=(HB→)ー(HA→) ……

④ 成分で表されたベクトル(平面)(空間)
⑤ 位置ベクトル
あえて書く必要もないのですが、③の応用で、機械的に、作業的に変形できるようにしていく。

〈例題1〉

基本となるベクトルで表しながら進めていくのはMethod!
基本となるベクトルは、Aが始点なので、A以外が始点のベクトルは減法を使って、始点をAにし、基本となるベクトルで表す。
(1) AC→は、ベクトルの連結で表せます。
(2) BD→は、A以外が始点のベクトルなので減法を使って、始点をAにします。
(4) DE→もA以外が始点のベクトルなので減法を使って、始点をAにします。
〈例題解答例1〉

〈問題2〉

〈問題解答例2〉
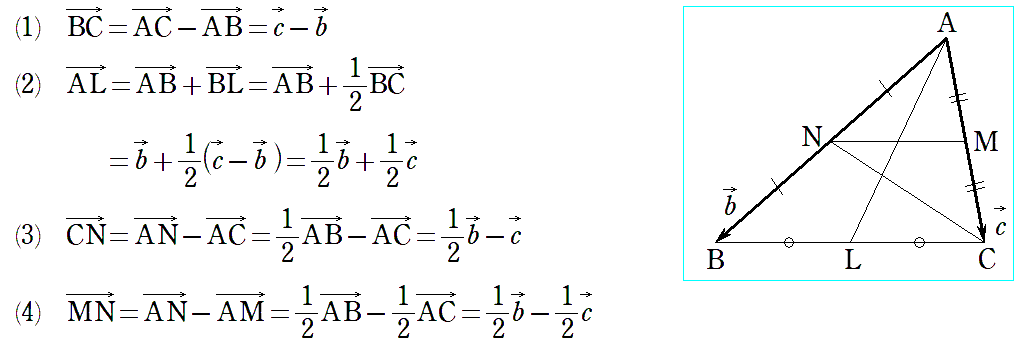
〈問題3〉

〈問題解答例3〉

〈問題4〉

〈問題解答例4〉

この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
