
ニューラルネットワークの仕組みが知りたい
この記事は、改定&整理統合されました。新版はこちら⬇です。
そもそもの始まりは「ディープラーニングAIはどのように学習し、推論しているのか」を読んだことにあります。当初は人工知能については利用者に徹しようと考えていました。しかし、生成AIのあまりにも魔法すぎる性能に驚愕するとともに頭の中で警鐘が鳴ったのです。 せめて人工知能がどのように動作しているのか概要くらいは知っておきたいと思って読んだのがこの本です。この本に出てくる数式と言えば$${y=ax+b}$$くらいでほぼ図と文章で説明し切ります(せいぜい7章にAIコードの説明用に短いPyTorchのコードが出てくるくらい)。素晴らしい!そうです、当初の考えではこの本で充分なハズだったのです。しかし、この本を読んでいて私の中で起こった意外な変化は「ニューラルネットワークにはパズル的な面白さがある。学習するニューロンを自分で作って観察してみたい。」だったのです。こうして、その思いを行動に移してニューラルネットワークを実装することにしました。結果的には力量をはるかに上回る難問パズルに挑戦することになったわけですが、ここまでの理解を記録に残しておきます。実装したニューラルネットワークには「Fiber」と名付けました。次のように使います。
model = Model(64, eta=0.01) # 入力層(入力数 = 64)
model.add(30, sigmoid, sigmoid_der) # 中間層(ニューロン数 = 30)
model.add(10, softmax) # 出力層(ニューロン数 = 10)
model.measurer(cat_xentropy, cat_accuracy) # 測定系の関数(損失関数、評価関数)を設定
model.fit(x_train, t_train, epochs=50, batch_size=50) # 最適化読み始める前に
ニューラルネットワークの実装を通じて分かったことを書いています。
実装に使用したプログラミング言語はPython 3です。
行列の演算を使用しない実装です。
実行環境はGoogle Colabです。動作確認も同様です。
ソースコードはGitHubにあります。[Open in Colab]アイコンをクリックするとすぐにGoogle Colabで実行できます。
最低限の数式が登場します。数式の展開は行わずに展開済みの結果を利用するだけです。
図解編
ニューラルネットワークには大きく分けると2つのデータの流れがあります。1つは順伝播でもう1つは逆伝播です。図解編では挫折ポイントである逆伝播(パラメータの更新を含む)のデータの流れを追いかけます。図に登場する数式、計算、関数は後続の「計算式編」と「実装編(その1) 関数」で整理します。
データフローダイアグラム(DFD)

図にある「パラメータ$${\!\!(w,b)\!}$$」はニューラルネットワークの最深部です。ここから矢印線を「パラメータの更新」に向かって遡っていくと次のようになります。
パラメータを更新するには「勾配」が必要。
勾配を計算するには「誤差」が必要。
誤差を計算するには「導関数」が必要。
遡ったところで、今度は下流に向かって「導関数と誤差」「勾配とパラメータの更新」の順に概要を見ていきます。
導関数と誤差
図から中間層と出力層では導関数付近のデータの流れが異なることが分かります。これは、中間層と出力層では次のように導関数の導出方法が異なることが影響しています。
▣ 出力層の場合
出力層では損失関数を微分して導関数を導出します。この導関数から誤差$${\!δ\!}$$を得ます。
▣ 中間層の場合
中間層では活性化関数を微分して導関数を導出します。この導関数から微分係数を得ることによって誤差$${\!δ\!}$$を計算します。
微分に際しては連鎖律(合成関数の微分)や偏微分(多変数関数の微分)を使いますが、導出済みの導関数を利用するので心配は要りません。
勾配とパラメータの更新
ニューラルネットワークにおいてパラメータを更新するには「傾き」ではなく「勾配」を利用します。下図は2次元空間のグラフとして作成しており、勾配を傾きのように表現しています。しかしながら現実のパラメータの更新は多次元空間で谷底(損失$${\!L\!}$$の最小化)を目指す作業になります。例えるなら、複雑な地形の山岳地帯で懐中電灯と足元の勾配を頼りに谷底を目指す作業になります。

勾配を知ることによって移動方向と移動量を決めることができます。常にゴールの谷底が見えない状態にありながら、勾配を頼りに少しずつ移動を繰り返します。そして、勾配がゼロに近づいたならば損失$${\!L\!}$$が最小となる谷底 🅰に到着している可能性があります。もしも運が悪ければ谷底 🅱に到着して抜け出せなくなっている可能性もありますが。その可能性を減らすためにいくつかの最適化アルゴリズムが考案されています。
手計算でパラメータを更新
Fiberの実装では行列による演算を使いません。普通であれば行列で一気に処理するようなところは自力で実装することになります。その部分については手計算から実装のイメージを掴むことにします。そうは言っても自力では出来ないので先達の力を借りることにします。欲しい物は「ニューラルネットワークの順伝播,逆伝播,確率的勾配降下法を手計算する$${^※}$$」にありました。
下図は参照先の記事にある手計算の結果を図に書き込んだものです。関係する流れをすべて図に書き込むと矢印線で埋まってしまうため適度に省略してあります。使用する記号や乗算の順序は参照先の記事に合わせてありますが、変更点が1つだけあります。原著では中間層の「重みの勾配」を計算するのに数式を1つだけ使っていますが、変更後は視覚的な分かり易さを狙ってこの数式を「入力の勾配」「誤差$${\!δ\!}$$」「重みの勾配」の3つに分けています。図の中央付近から上に向かっていく流れがそれです。
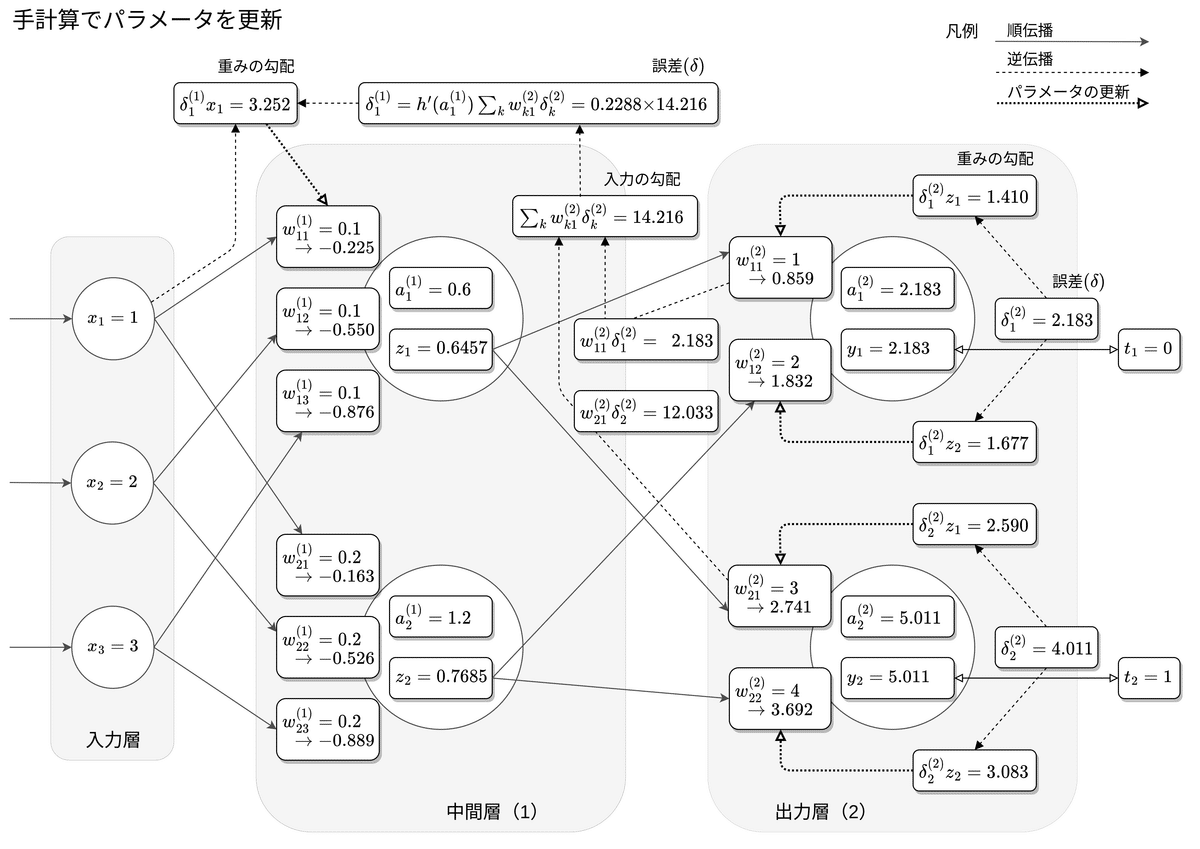
$${^※}$$この手計算は、図解編とは別に動作確認編でも活用させていただいたので本当に役に立ちました。著者には感謝しか無いです。
連鎖律を使って式を立てる
図解編の締め括りは連鎖律です。この後で計算式を整理しますが少しでも連鎖律の図に目を通しておくと驚くほど数式の見え方が鮮明になると思います。図の作成に当たっては1番最初に登場したデータフローダイアグラム(DFD)をベースにして数式を記入しました。図では例として重み$${\!w\!}$$の勾配を求める式を立てています。

計算式編
パラメータの更新に必要な計算式を整理します。ニューラルネットワークの説明に使われる数式は複雑ですが、最終的に得られる数式はシンプルになるように工夫されているのでそれを最大限に享受します。ここでは数式をFiberの実装に困らないレベルまで削ぎ落としています。数式の展開は連鎖律から先をすっ飛ばして結果だけを載せます。記号($${x,\,y,\,t,\,u,\,w,\,b,\,δ}$$)については図解編のデータフローダイアグラム(DFD)を参照すると理解の助けになります。
誤差の計算
誤差$${\!δ\!}$$の計算方法は、出力層と中間層で異なります。
▣ 出力層: 誤差$${\!δ\!}$$ = 予測値$${\!y\!}$$ − 正解値$${\!t\!}$$
$$
\tag{2.1}δ=\cfrac{∂L}{∂u}=\cfrac{∂L}{∂y} \cfrac{∂y}{∂u}=\ldots=y-t
$$
▣ 中間層: 誤差$${\!δ\!}$$ = 入力$${\!x\!}$$の勾配$${^※}$$ × 導関数
$$
\tag{2.2}δ=\cfrac{∂L}{∂u}=\cfrac{∂L}{∂x} \cfrac{∂y}{∂u}=\ldots
=\displaystyle\sum_kδ_kw_kf'(u)
$$
$${^※}$$入力$${\!x\!}$$の勾配は逆伝播で伝わってくる情報です。
勾配の計算
▣ 入力$${\!x\!}$$の勾配 = 誤差$${\!δ\!}$$ × 重み$${\!w\!}$$ の総和
入力$${\!x\!}$$について損失関数を偏微分します。
$$
\tag{2.3}\cfrac{∂L}{∂x}=\cfrac{∂L}{∂u} \cfrac{∂u}{∂x}=\ldots=\displaystyle\sum_kδ_kw_k
$$
▣ 重み$${\!w\!}$$の勾配 = 誤差$${\!δ\!}$$ × 入力値$${\!x\!}$$
重み$${\!w\!}$$について損失関数を偏微分します。
$$
\tag{2.4}\cfrac{∂L}{∂w}=\cfrac{∂L}{∂u} \cfrac{∂u}{∂w}=\ldots=δx
$$
▣ バイアス$${\!b\!}$$の勾配 = 誤差$${\!δ\!}$$
バイアス$${\!b\!}$$について損失関数を偏微分します。
$$
\tag{2.5}\cfrac{∂L}{∂b}=\cfrac{∂L}{∂u} \cfrac{∂u}{∂b}=\ldots=δ
$$
パラメータの更新
パラメータを更新するには勾配降下法(最急降下法)の式を使います。パラメータの更新は勾配の計算が終わっていれば簡単です。
▣ 重み$${\!w\!}$$ = 重み$${\!w\!}$$ − 学習率$${\!η\!}$$ × 重み$${\!w\!}$$の勾配
$$
\tag{2.6}w←w-η\cfrac{∂L}{∂w}=w-ηδx
$$
▣ バイアス$${\!b\!}$$ = バイアス$${\!b\!}$$ − 学習率$${\!η\!}$$ × バイアス$${\!b\!}$$の勾配
$$
\tag{2.7}b←b-η\cfrac{∂L}{∂b}=b-ηδ
$$
実装編(その0)
Fiberの基本的な機能は ①モデルの構築 ②最適化 ③評価 ④予測 の4つです。まずはこれらの機能を実装する上での軸を定めておきます。
全体の構造
Fiberはクラスとその外部にある関数の集合体として構成します。Fiberの本体は4つのクラス(ニューロン、レイヤ、コーテクス、モデル)で構成します。ニューラルネットワークは複数の関数が連携して動作しますが、これらの関数はクラスの外部に用意します。Fiberの本体はこれらの関数を連携させる司令塔の役割を持ちます。外部の関数としては例えば活性化関数、導関数、損失関数、評価関数などがあります。モデルを構築するときには問題の特徴に合わせて適切な関数を選択できるような作りにします。
教師あり学習
Fiberは教師あり学習について演習が可能な枠組みを用意します。
▣ ロジスティック回帰
二値分類と多値分類の両方の問題に適用できます。
▣ 線形回帰
単回帰と重回帰のいずれの問題にも適用できません。ニューラルネットワーク自体は線形回帰の問題に適用できるのですが、Fiberでは線形回帰の演習に必要な充分な枠組みを用意しません。具体的な例を1つだけ挙げると、回帰直線をグラフ表示するには係数と切片を取得する機能が必要ですがFiberには実装しません。
アルゴリズム
▣ 勾配の計算手法
勾配の計算手法は誤差逆伝播法(バックプロパゲーション)に固定します。
▣ 最適化アルゴリズム
最適化アルゴリズムは確率的勾配降下法(SGD)に固定します。
ミニバッチ学習
Fiberのミニバッチ学習は、行列演算で実装されたミニバッチ学習を模倣しようとしたものです。しかし両者の仕組みは根本的に異なるのでFiberの実装はミニバッチ学習モドキくらいに捉えていただくのが良いと思います。
ミニバッチ学習を実現するためにデータセットからデータをランダムに取り出すためのインデックスを作成します。このインデックスはランダムになっているだけではなくミニバッチ学習を想定した構造になっています。ミニバッチ学習は他の学習単位であるバッチ学習とオンライン学習を模倣することが出来ます。バッチサイズをデータセットと同じ件数に設定するとバッチ学習になり、バッチサイズを1に設定するとオンライン学習になります。
ライブラリのインポートなど
そろそろ実装を始めましょう。まずは、ライブラリのインポートから。
#--------------------------------------------------
# 必須ライブラリ
#--------------------------------------------------
import numpy as np
#--------------------------------------------------
# データを可視化
#--------------------------------------------------
import matplotlib.pyplot as plt
import pandas as pd
#--------------------------------------------------
# データセットの取得とデータの前処理
#--------------------------------------------------
import seaborn as sns
from sklearn.datasets import load_iris
from sklearn.datasets import load_digits
import sklearn.preprocessing as prep
#--------------------------------------------------
# FiberとKerasの動作を比較
#--------------------------------------------------
from tensorflow import keras
#--------------------------------------------------
# ユーティリティ
#--------------------------------------------------
class Object: pass # 最小限のオブジェクトを生成
def judge(flag): # 論理値を判定文字列に変換
return '✓ PASS' if flag else '✗ FAIL'
#--------------------------------------------------
# 動作環境の設定
#--------------------------------------------------
%config InlineBackend.figure_format = 'retina' # 図の描画を高精細に
np.set_printoptions(formatter={'float':'{: .8f}'.format}) # 数値の表示を整える実装編(その1) 関数
ニューラルネットワークでは要所ごとに関数(活性化関数、損失関数など)が登場します。これらの関数に対してもまた様々なアルゴリズムが考案されています。ここに登場する関数は次の通りです。
線形変換関数 ― affine関数/linear関数
初期化関数 ― glorot_uniform関数/he_normal関数/xavier_normal関数
活性化関数 ― sigmoid関数/tanh関数/ReLU関数/softmax関数/恒等関数
導関数 ― sigmoid関数の導関数/tanh関数の導関数/ReLU関数の導関数/損失関数の導関数
損失関数 ― 二乗和誤差関数/二値交差エントロピー関数/交差エントロピー関数
評価関数 ― 正解率(二値)/正解率(多値)
線形変換関数
線形変換関数は(活性化関数を通す前の)ニューロンの出力値$${\!u\!}$$を計算します。@演算子で重みベクトルと入力ベクトルのドット積(内積)を計算しています。
#--------------------------------------------------
# _fneu_ ← 線形変換関数(linear transformation function)
#--------------------------------------------------
def affine(w, x, b): # バイアスを含む(デフォルト)
return w @ x + b
def linear(w, x, b): # バイアスを含まない
return w @ x▣ affine関数
通常はバイアスを含めて計算するのでFiberはデフォルトでaffine関数を呼び出します。
$$
\tag{3.1.1}u=w\cdot x+b
$$
▣ linear関数
動作確認編では重みの影響だけを追跡したいのでlinear関数を使っています。
$$
\tag{3.1.2}u=w\cdot x
$$
初期化関数
初期化関数はパラメータ(重み)の初期化で使用する乱数を出力します。もう1つのパラメータであるバイアスの初期化でも乱数を使用しますが、そちらについては 平均値$${=0.0}$$、標準偏差$${=0.1}$$の正規分布に固定しました。
パラメータを0や1のような適当な数値で初期化してしまうと全く最適化できないということが起こります。そのため効率よくパラメータを最適化するには良く考えられた初期化関数が必要です。
#--------------------------------------------------
# _fini_ ← 初期化関数(initialization function)
#--------------------------------------------------
def glorot_uniform(nodes, links): # glorot uniform(デフォルト)
min = -np.sqrt(6 / (nodes + links))
max = np.sqrt(6 / (nodes + links))
return np.random.uniform(min, max, (nodes, links))
def he_normal(nodes, links): # he normal (for ReLU)
std = np.sqrt(2 / links)
return np.random.normal(0.0, std, (nodes, links))
def xavier_normal(nodes, links): # xavier normal (for sigmoid, tanh)
std = 1 / np.sqrt(links)
return np.random.normal(0.0, std, (nodes, links))▣ glorot_uniform関数(デフォルト)
一様分布(計算方法は実装を参照)
▣ he_normal関数
正規分布、平均値$${=0.0}$$、標準偏差$${\displaystyle=\sqrt{\frac{2}{n}}}$$
▣ xavier_normal関数
正規分布、平均値$${=0.0}$$、標準偏差$${\displaystyle=\frac{1}{\sqrt{n}}}$$
これらの初期化関数と活性化関数には相性があります。例えば活性化関数にReLU関数を使うなら初期化関数にはhe_normal関数を使うと良いとされています。相性は次の通りですがデフォルト(glorot_uniform関数)のままでもそれなりに動きます。
ReLU関数 ⇔ he_normal関数
sigmoid関数、tanh関数 ⇔ xavier_normal関数
初期化関数について散布図とヒストグラムを見ておきます。なお散布図については2分割した乱数群をそれぞれ$${x}$$軸と$${y}$$軸に割り当てて作成しています。
nodes = 40
links = 40
funcs = [
('glorot_uniform', glorot_uniform(nodes, links)),
('he_normal', he_normal(nodes, links) ),
('xavier_normal', xavier_normal(nodes, links) )
]
plt.figure(figsize=(8, 16))
plt.subplots_adjust(wspace=0.2, hspace=0.3)
for (i, func) in enumerate(funcs):
plt.subplot(4, 2, i*2 + 1) # 散布図
plt.title(func[0])
plt.xlim(-0.5, 0.5)
plt.ylim(-0.5, 0.5)
plt.scatter(func[1][:20], func[1][20:], 8)
plt.subplot(4, 2, i*2 + 2) # ヒストグラム
plt.title(func[0])
plt.xlim(-0.5, 0.5)
plt.ylim(0, 15)
plt.hist(func[1])
plt.show()
活性化関数
活性化関数は、線形変換関数の出力(=ニューロンの出力)を活性化します。
ニューラルネットワークではその前身のパーセプトロンと違って微分可能な活性化関数を使います。これにより誤差逆伝播法が実現可能になりました。つまり活性化関数は微分できるという点が重要です。この活性化関数に続いて導関数が登場しますがこれは活性化関数を微分したものです。
#--------------------------------------------------
# _fact_ ← 活性化関数(activation function)
#--------------------------------------------------
def sigmoid(x): # sigmoid関数
return 1 / (1 + np.exp(-x))
def tanh(x): # tanh関数
return np.tanh(x)
def relu(x): # ReLU関数
return np.maximum(0, x)
def softmax(x): # softmax関数
exps = np.exp(x - np.max(x)) # オーバーフローを防ぐために各要素から最大値をマイナス
return exps / np.sum(exps)
def identity(x): # 恒等関数
return x▣ sigmoid関数
sigmoid関数は入力に対して0から1までの間の値を返します。二値分類において出力層でsigmoid関数を使うと出力値を確率値のように利用できます。例えば陽性/陰性の診断で、陽性の可能性が$${0.83(83\%)}$$のような使い方です。
$$
\tag{3.3.1}f(x)=\cfrac{1}{1+\exp(-x)}
$$
▣ tanh関数
tanh関数は入力に対して-1から1までの間の値を返します。sigmoid関数と似ていますが学習効率や勾配消失問題の点でメリットが知られています。演習では使っていませんが切れ味を試してみたいので残してあります。
$$
\tag{3.3.2}f(x)=\cfrac{e^x - e^{-x}}{e^x + e^{-x}}
$$
▣ ReLU関数
ReLU関数は入力が0以下だと0を出力しますが、0よりも大きい場合は入力された値をそのまま返します。tanh関数と同様に学習効率や勾配消失問題の点でメリットが知られており、中間層で良く使われています。
$$
\tag{3.3.3}f(x)=\begin{cases}
x & (x\gt 0)
\\
0 & (x\leqq 0)
\end{cases}
$$
▣ softmax関数
softmax関数は入力されたベクトルと同じ次数のベクトルに0から1までの間の値をセットして返します。また、ベクトルの要素をすべて足し合わせると1になるという特徴があります。多値分類において出力層でsoftmax関数を使うと出力値を確率値のように利用できます。例えば動物写真の分類で、猫の可能性が$${0.17(17\%)}$$、犬の可能性が$${0.70(70\%)}$$、兎の可能性が$${0.13(13\%)}$$のような使い方です。
$$
\tag{3.3.4}\displaystyle y=\frac{\exp(x)}{\displaystyle\sum_{k}\exp(x_k)}
$$
▣ 恒等関数
恒等関数は入力された値をそのまま返します。主に回帰問題の出力層で使われます。Fiberでは動作確認編で使っています。
$$
\tag{3.3.5}f(x)=x
$$
sigmoid関数、tanh関数、ReLU関数 をグラフで比較します。
x = np.arange(-5.0, 5.0, 0.1)
funcs = [
('sigmoid', sigmoid(x)),
('tanh', tanh(x)),
('relu', relu(x))
]
plt.ylim(-1.1, 1.9)
plt.ylabel(r'$f(x)$', size=16, math_fontfamily='cm')
plt.xlabel(r'$x$', size=16, math_fontfamily='cm')
plt.grid()
for func in funcs:
plt.plot(x, func[1], label=func[0])
plt.legend()
plt.show()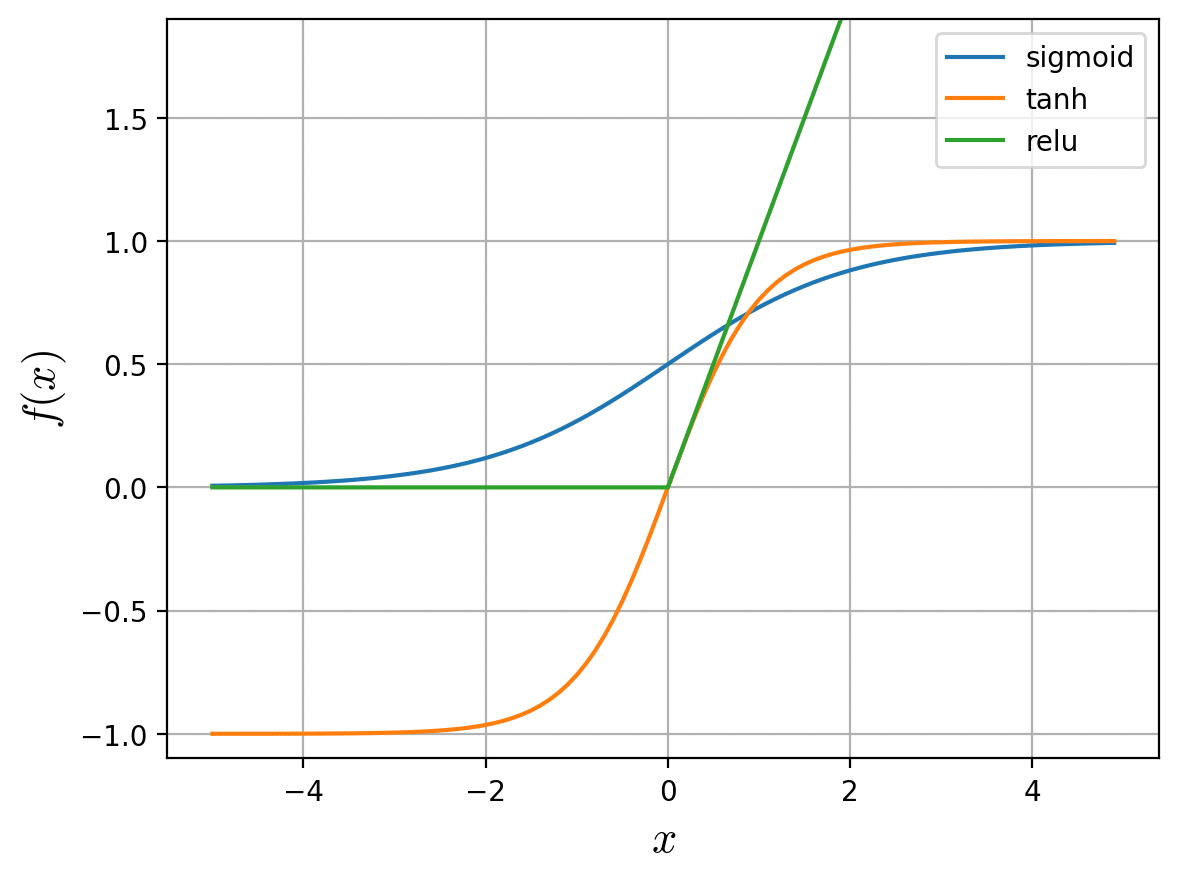
導関数
4つの導関数のうち最初の3つは活性化関数(sigmoid関数、tanh関数、ReLU関数)から導出されています。残りの1つは損失関数から導出されています。
Fiberではモデルにレイヤを追加するときに活性化関数と導関数をペアにして指定します。そうしたければFiberに予め用意されている活性化関数(と導関数)とは別の関数を利用することもできます。ただし、損失関数の導関数についてはFiberから固定的に呼び出します。
#--------------------------------------------------
# _fder_ ← 導関数(derivative function)
#--------------------------------------------------
def sigmoid_der(x): # sigmoid関数の導関数
return sigmoid(x) * (1.0 - sigmoid(x))
def tanh_der(x): # tanh関数の導関数
return 1.0 - (tanh(x) ** 2)
def relu_der(x): # ReLU関数の導関数
return np.where(x > 0, 1, 0)
def loss_der(y, t): # 損失関数の導関数
return y - t▣ sigmoid関数の導関数
$$
\tag{3.4.1}f'(x)=f(x)(1-f(x))
$$
▣ tanh関数の導関数
$$
\tag{3.4.2}f'(x)=1-f(x)^2
$$
▣ ReLU関数の導関数
$$
\tag{3.4.3}f'(x)=\left\{\begin{array}{cc} 1 & (x\gt 0) \\ 0 & (x\leqq 0) \end{array}\right.
$$
▣ 損失関数の導関数
$$
\tag{3.4.4}f'(y,t)=y-t
$$
sigmoid関数、tanh関数、ReLU関数のそれぞれの導関数をグラフで比較します。
x = np.arange(-5.0, 5.0, 0.1)
funcs = [
('sigmoid_der', sigmoid_der(x)),
('tanh_der', tanh_der(x)),
('relu_der', relu_der(x))
]
plt.ylim(-0.2, 1.2)
plt.ylabel(r"$f'(x)$", size=16, math_fontfamily='cm')
plt.xlabel(r'$x$', size=16, math_fontfamily='cm')
plt.grid()
for func in funcs:
plt.plot(x, func[1], label=func[0])
plt.legend()
plt.show()
入力に対して出力がゼロに近くなるところでは、これに引き摺られて誤差$${\!δ\!}$$の計算結果もゼロに近くなります。ニューラルネットワークの最適化では誤差$${\!δ\!}$$を利用するので、このことが最適化がうまく進まなくなる原因になります。これを勾配消失問題と言います。
損失関数
損失関数は次に登場する評価関数とは指標という点で似ています。しかし、損失関数と評価関数には決定的な違いがあって、損失関数は微分するとパラメータを最適化するための指標にできます。
損失関数には他にも呼び名があって、誤差関数、目的関数、コスト関数などとも呼ばれています。
#--------------------------------------------------
# _flos_ ← 損失関数(loss function)
#--------------------------------------------------
def sse(y, t): # 二乗和誤差関数
return 0.5 * np.sum((y - t) ** 2)
def bin_xentropy(y, t): # 二値交差エントロピー関数
return float(-t * np.log(y) - (1 - t) * np.log(1 - y))
def cat_xentropy(y, t): # 交差エントロピー関数
delta = 1e-7 # ゼロ除算を防ぐための微小な値
return -np.sum(t * np.log(y + delta))▣ 二乗和誤差関数
動作確認編(手計算を再現)で使用します。
$$
\tag{3.5.1}L=\cfrac{1}{2}\sum_{k}(y_k-t_k)^2
$$
▣ 二値交差エントロピー関数
演習編(二値分類)で使用します。
$$
\tag{3.5.2}L=-t\log y-(1-t)\log(1-y)
$$
▣ 交差エントロピー関数
演習編(多値分類)で使用します。
$$
\tag{3.5.3}L=-\sum_{k}t_k\log y_k
$$
評価関数
評価関数はモデルの性能を定量的に測定して評価指標を提供します。評価指標には、正解率、適合率、再現率、F値、ROC曲線、AUC値など様々なものがありますが、Fiberの演習では正解率が分かれば充分です。演習では二値分類と多値分類を行いますが両者では正解の判定方法が異なるので評価関数は2つに分かれています。
#--------------------------------------------------
# _feva_ ← 評価関数(evaluation function)
#--------------------------------------------------
def bin_accuracy(y, t): # 正解率(二値)
def isequal(y, t):
return 1 if np.round(y) == np.round(t) else 0
return np.mean([isequal(y, t) for (y, t) in zip(y, t)])
def cat_accuracy(y, t): # 正解率(多値)
def isequal(y, t):
return 1 if np.argmax(y) == np.argmax(t) else 0
return np.mean([isequal(y, t) for (y, t) in zip(y, t)])▣ 正解率(二値)
予測値と正解値のそれぞれを四捨五入(銀行家の丸め)してから比較します。
▣ 正解率(多値)
予測値ベクトルと正解値ベクトルのそれぞれから最大値を指す要素番号を取得して比較します。
関数の使い分け(出力層)
二値分類と多値分類のどちらを行うかによって出力層で使用する活性化関数を使い分けます。また損失関数と評価関数は活性化関数に対応するものを使います。
▣ 二値分類での組み合わせ(出力層)
活性化関数: sigmoid関数
損失関数 : bin_xentropy関数
評価関数 : bin_accuracy関数
▣ 多値分類での組み合わせ(出力層)
活性化関数: softmax関数
損失関数 : cat_xentropy関数
評価関数 : cat_accuracy関数
実装編(その2) 本体
Fiberの本体は4つのクラス(ニューロン、レイヤ、コーテクス、モデル)で構成されています。
ニューロン
Fiberではパラメータ$${\!(w,b)\!}$$をニューロンの配下にあるものとして扱います。ニューロンは線形変換関数を呼び出すことによって出力値$${\!u\!}$$を計算します。線形変換関数に続けて活性化関数も連続で呼び出して良いと思うかも知れませんが、活性化関数の中にはsoftmax関数のようにレイヤ全体に作用するものもあるので、活性化関数の呼び出しはレイヤから実行します。ニューロンには計算式編で示した勾配の計算とパラメータの更新も実装されています。
ニューロンの実装イメージは図解編の「手計算でパラメータを更新」の図ががそれに当たります。この図にあるニューロンが自律的に動いている様子をイメージしながら実装してみました。行列による演算で実装するとニューロンが消えて重みだけが残るので機械的過ぎて寂しいです。ニューロンが存在することにより実装に愛着が湧きますが、その反面処理が重くなるので非常に贅沢な実装と言えます。
#--------------------------------------------------
# ニューロン(パラメータを管理)
#--------------------------------------------------
class Neuron:
def __init__(self, env, core):
self.w = core # 重みの一覧
self.b = np.random.normal(0.0, 0.1) # バイアス(1個)
self._fneu_ = env.fneu # ニューロンが使用する関数(1個)を確定
self.eta = env.eta # 学習率
self.grad_w = [] # 重みの勾配を蓄積(ミニバッチ対応)
self.grad_b = [] # バイアスの勾配を蓄積(ミニバッチ対応)
def output(self, x): # ニューロンの出力を計算
return self._fneu_(self.w, x, self.b) #⬅ _fneu_(線形変換関数)
def calcgrad(self, x, delta): # 勾配を計算
self.grad_w.append(x * delta) # 重みの勾配
self.grad_b.append(delta) # バイアスの勾配
return self.w * delta # 逆伝播させる入力の勾配(レイヤで結線どおりに合算する)
def update(self): # パラメータを更新
self.w -= np.sum(self.grad_w, axis=0) * self.eta # 重みを更新
self.b -= np.sum(self.grad_b, axis=0) * self.eta # バイアスを更新
self.grad_w = []
self.grad_b = []レイヤ
レイヤはコーテクスとニューロンの間の橋渡し的な存在です。コーテクスからレイヤに信号が渡されるとレイヤ自身が所有しているニューロンに処理を依頼します。そして、ニューロンの処理結果を他のレイヤに渡せるように集約します。
レイヤには入力層、中間層、出力層といった区別がありません。そもそも入力層にはニューロンがないので実装には現れません。また、中間層と出力層の違いはコーテクスが吸収します。図解編のデータフローダイアグラム(DFD)には中間層と出力層の違いが表現されていますが、実装レベルで考えた場合はレイヤにそのような違いを実装するよりもコーテクスに任せた方がエレガントなのです。
レイヤはこのようにシンプルな存在でありながらモデルを構築するときに威力を発揮します。なぜなら、モデルの骨組みはレイヤを追加して行くことによって組み立てられるからです。
#--------------------------------------------------
# レイヤ(ニューロンを管理)
#--------------------------------------------------
class Layer:
def __init__(self, fun, env, nodes, links):
self.neurons = [] # ニューロンの一覧(nodes個)
(self._fact_, self._fder_, self._fini_) = fun # レイヤが使用する関数(3個)を確定
self.x = [] # レイヤへの入力 (逆伝播において勾配の計算で使用)
self.u = [] # ニューロンからの出力(逆伝播において誤差の計算に使用)
for core in self._fini_(nodes, links): #⬅ _fini_(初期化関数)/coreにはlinks個の乱数が入る
self.neurons.append(Neuron(env, core)) # ニューロンを生成して一覧に追加する
def output(self, x): # レイヤからの出力を計算
self.x = x # レイヤへの入力を保存
self.u = np.array([neuron.output(self.x) for neuron in self.neurons]) # ニューロンに出力の計算を依頼する
return self._fact_(self.u) #⬅ _fact_(活性化関数)/この計算結果が次のレイヤに渡される
def calcgrad(self, delta): # 入力の勾配を計算
grad_x = [] # 入力の勾配を蓄積
for (neuron, delta) in zip(self.neurons, delta):
grad_x.append(neuron.calcgrad(self.x, delta)) # ニューロンに勾配の計算を依頼する
return np.sum(grad_x, axis=0) # 蓄積した入力の勾配をリンクの結線どおりに合算
def update(self): # パラメータを更新
for neuron in self.neurons:
neuron.update() # ニューロンにパラメータの更新を依頼するコーテクス
コーテクスはレイヤをコントロールして順伝播や逆伝播を実行します。コーテクスには入力$${\!x\!}$$の勾配を逆伝播させる処理が実装されています。また、逆伝播で必要になる誤差$${\!δ\!}$$の計算を行っています。
#--------------------------------------------------
# コーテクス(レイヤを管理)
#--------------------------------------------------
class Cortex:
def __init__(self, links, eta, fneu):
self.layers = [] # レイヤの一覧
self.links = links # 最初のレイヤの1ニューロンに接続されるリンクの数
self.env = Object() # ニューロンの動作を規定する環境変数
self.env.eta = eta # 学習率
self.env.fneu = fneu # 線形変換関数
def add(self, nodes, fun): # レイヤを追加
self.layers.append(Layer(fun, self.env, nodes, self.links)) # レイヤを生成して一覧に追加する
self.links = nodes # 次のレイヤの1ニューロンに接続されるリンクの数
def forward(self, x): # 順伝播
for layer in self.layers: # 深層対応ループ(出力層に向かって行く)
x = layer.output(x)
return x # 最終レイヤ(出力層)からの出力値を返す
def backward(self, delta): # 逆伝播
layers = list(reversed(self.layers)) # レイヤを逆順に並べる
grad_x = layers[0].calcgrad(delta) # 最終レイヤ(出力層)の勾配を計算
for layer in layers[1:]: # 深層対応ループ(入力層に向かって行く)
delta = grad_x * layer._fder_(layer.u) #⬅ _fder_(導関数)/入力の勾配から誤差を計算
grad_x = layer.calcgrad(delta) # 中間層の勾配を計算
def onecycle(self, x, t): # 順伝播と逆伝播を1サイクルだけ実行
y = self.forward(x) # 順伝播
delta = loss_der(y, t) #⬅ loss_der(導関数)/誤差を計算
self.backward(delta) # 逆伝播
return y # 予測値を返す
def update(self): # パラメータを更新
for layer in self.layers:
layer.update() # レイヤにパラメータの更新を依頼するモデル
モデルには最適化アルゴリズムと測定系の処理が実装されています。他の3つのクラス(ニューロン、レイヤ、コーテクス)はモデルの配下で完結するため、Fiberを演習で使用する段階ではモデルが提供する機能(メソッド)だけを意識することになります。メソッドは次の通りです。
add ― レイヤを追加
レイヤを生成してその中に指定された数のニューロンを生成します。measurer ― 測定系の関数を設定
損失関数と評価関数を設定します。fit ― 最適化
最適化アルゴリズムに基づいてパラメータを最適化します。evaluate ― 評価
順伝播を実行して損失と精度の測定結果(評価指標)を返します。predict ― 予測
順伝播を実行して予測(再現、推測、認識)結果を返します。
#--------------------------------------------------
# モデル
#--------------------------------------------------
class Model:
def __init__(self, nw, eta, fneu=affine):
self.cortex = Cortex(nw, eta, fneu) # モデルが使用するコーテクスを1個確保
self._flos_ = None
self._feva_ = None
@staticmethod
def idx_mini(num, batch_size): # ミニバッチ用のシャッフルされたインデックスを作成
shuffle = np.random.permutation(num) # シャッフル
return [shuffle[i:i+batch_size] for i in range(0, num, batch_size)] # ミニバッチ形式に変換
@staticmethod
def show_progress(epo, epochs, hist): # 最適化の進行状況を表示
print(f'epoch = {epo+1:>4d} / {epochs:>4d}, ', end='')
print(f'loss = {hist.loss[-1]:.8f}, ', end='')
print(f'accu = {hist.accu[-1]:.8f}')
def add(self, nodes, fact, fder=lambda x:None, fini=glorot_uniform): # レイヤを追加
fun = (fact, fder, fini) # レイヤが使用する関数群
self.cortex.add(nodes, fun) # コーテクスにレイヤの追加を依頼
def measurer(self, flos, feva): # 測定系の関数を設定
self._flos_ = flos # 損失関数(モデルが使用する関数(1/2個)を確定)
self._feva_ = feva # 評価関数(モデルが使用する関数(2/2個)を確定)
def fit(self, x, t, epochs, batch_size, verbose=0): # 最適化
hist = Object()
hist.loss = [] # 損失の履歴(最終的な結果)
hist.accu = [] # 精度の履歴(最終的な結果)
for epo in range(epochs): # エポック開始
loss, pred, targ = [], [], [] # 損失・予測値・正解値の履歴(1エポックの計算で使用)
whole = self.idx_mini(len(x), batch_size) # ミニバッチ用のシャッフルされたインデックスを作成
for mini in whole: # すべてのミニバッチが終了するまで繰り返す
for i in mini: # ミニバッチ開始
y = self.cortex.onecycle(x[i], t[i]) # 順伝播と逆伝播を1サイクルだけ実行
loss.append(self._flos_(y, t[i])) #⬅ _flos_(損失関数)/損失の履歴を更新
pred.append(y) # 予測値の履歴を更新
targ.append(t[i]) # 正解値の履歴を更新
self.cortex.update() # ミニバッチ終了、パラメータを更新
hist.loss.append(np.mean(loss)) # 損失の履歴を更新
hist.accu.append(self._feva_(pred, targ)) #⬅ _feva_(評価関数)/精度の履歴を更新
if verbose: self.show_progress(epo, epochs, hist) # 最適化の進行状況を表示
return hist
def evaluate(self, vx, vt): # 評価
loss, pred = [], [] # 損失・予測値の履歴
for (x, t) in zip(vx, vt):
y = self.cortex.forward(x) # 順伝播
loss.append(self._flos_(y, t)) #⬅ _flos_(損失関数)/損失の履歴を更新
pred.append(y)
eval = Object()
eval.loss = np.mean(loss) # 損失を計算(平均)
eval.accu = self._feva_(pred, vt) #⬅ _feva_(評価関数)/精度を計算
return eval
def predict(self, whole): # 予測
pred = [] # 予測値の履歴
for x in whole:
pred.append(self.cortex.forward(x)) # 順伝播/予測値の履歴を更新
return pred動作確認編
演習に入る前に最低限の動作を確認しておきます。動作確認では次の2パターンについてFiber以外の処理系と比較します。特に後者では著名なフレームワークのKerasと比較しているので安心感が増します。
手計算を再現(2層)
現実的な更新(3層)
動作確認をサポートするユーティリティ
次の4つのユーティリティが動作確認をサポートします。
CoreFiber ― Fiberの重みをダイレクトに操作
CoreKeras ― Kerasの重みをダイレクトに操作
show_coredump ― 重みを表示
show_corediff ― 重みの差分が許容範囲内であれば「PASS」
#--------------------------------------------------
# Fiberの重みをダイレクトに操作
#--------------------------------------------------
class CoreFiber:
@staticmethod
def coreinit(model, w): # 重みを初期化
for (lno, layer) in enumerate(model.cortex.layers):
for (nno, neuron) in enumerate(layer.neurons):
neuron.w = np.array(w[lno][nno])
@staticmethod
def coredump(model): # 重みの現在値を出力
whole = []
for layer in model.cortex.layers:
whole.append([neuron.w.tolist() for neuron in layer.neurons])
return whole
#--------------------------------------------------
# Kerasの重みをダイレクトに操作
#--------------------------------------------------
class CoreKeras:
@staticmethod
def coreinit(model, w): # 重みを初期化
for (i, w) in enumerate(w):
model.layers[i].set_weights([w])
@staticmethod
def coredump(model): # 重みの現在値を出力
whole = []
for layer in model.layers:
whole.append(layer.get_weights()[0])
return whole
#--------------------------------------------------
# 重みを表示
#--------------------------------------------------
def show_coredump(core):
for (i, core) in enumerate(core):
print(np.array(core))
#--------------------------------------------------
# 重みの差分が許容範囲内であれば「PASS」
#--------------------------------------------------
def show_corediff(w1, w2, limit):
result = []
for (w1, w2) in zip(w1, w2): # レイヤごとに重みの差を表示
w1 = np.array(w1)
w2 = np.array(w2)
diff = np.abs(w1 - w2)
result.append(np.all(diff < limit)) # 許容範囲内ならTrueを追加
print(diff)
print(f'許容できる差分の限界: {limit}')
for (i, result) in enumerate(result): # レイヤごとに判定結果を表示
print(f'Layer {i}: {judge(result)}')手計算を再現(2層)
3つの処理系(Fiber、素朴な実装、手計算)で重みの更新結果を比較します。使用するデータセットは図解編の手計算と同じものです。重みの更新が終わったところで次の2パターンについて全ての重みを比較します。
Fiber vs. 素朴な実装(行列による実装)
Fiber vs. 手計算(図解編の手計算)
#--------------------------------------------------
# 手計算を再現(Fiber)
#--------------------------------------------------
def hcalc_Fiber(w, x_train, t_train, eta):
core = CoreFiber
model = Model(3, eta, linear) # 入力層(入力数 = 3)
model.add(2, sigmoid, sigmoid_der) # 中間層(ニューロン数 = 2)
model.add(2, identity) # 出力層(ニューロン数 = 2)
model.measurer(sse, cat_accuracy) # 測定系の関数(損失関数、評価関数)を設定
core.coreinit(model, w)
model.fit(x_train, t_train, epochs=1, batch_size=1)
return core.coredump(model)
#--------------------------------------------------
# 手計算を再現(素朴な実装―2層)
#--------------------------------------------------
def hcalc_Plain_2Layer(w, x_train, t_train, eta):
w_mi1 = w[0].copy().T # 重みを初期化
w_out = w[1].copy().T
y_mi1 = sigmoid(x_train @ w_mi1) # 順伝播
y_out = identity(y_mi1 @ w_out)
dlt_out = y_out - t_train # 逆伝播
dlt_mi1 = (dlt_out @ w_out.T) * sigmoid_der(x_train @ w_mi1)
w_out -= eta * np.outer(y_mi1, dlt_out) # 重みを更新
w_mi1 -= eta * np.outer(x_train, dlt_mi1)
return [w_mi1.T, w_out.T]
#--------------------------------------------------
# 動作確認(手計算を再現)
#--------------------------------------------------
ini_w0 = np.array([ # 中間層の重み(初期値)
[0.1, 0.1, 0.1],
[0.2, 0.2, 0.2]
])
ini_w1 = np.array([ # 出力層の重み(初期値)
[1.0, 2.0],
[3.0, 4.0]
])
hnd_w0 = np.array([ # 中間層の重み(手計算で算出)
[-0.225237618, -0.550475236, -0.875712854],
[-0.163076931, -0.526153862, -0.889230793]
])
hnd_w1 = np.array([ # 出力層の重み(手計算で算出)
[ 0.859072219, 1.832253644],
[ 2.741022862, 3.691739479]
])
ini_w = [ini_w0, ini_w1]
hnd_w = [hnd_w0, hnd_w1]
x_train = np.array([ [1, 2, 3] ]) # 特徴量データ
t_train = np.array([ [0, 1] ]) # 正解値データ
limit = 1e-8 # 許容できる差分の限界
eta = 0.1 # 学習率
nnm_w = hcalc_Fiber(ini_w, x_train, t_train, eta)
pln_w = hcalc_Plain_2Layer(ini_w, x_train, t_train, eta)
print('Fiberが算出した重み')
show_coredump(nnm_w)
print('\n素朴な実装が算出した重み')
show_coredump(pln_w)
print('\n手計算で算出した重み')
show_coredump(hnd_w)
print('\n重みの差分(Fiber vs. 素朴な実装)')
show_corediff(nnm_w, pln_w, limit)
print('\n重みの差分(Fiber vs. 手計算)')
show_corediff(nnm_w, hnd_w, limit)

結果は、重みの差分が許容範囲内$${(10^{-8})}$$なので問題無しとしました。
現実的な更新(3層)
3つの処理系(Fiber、素朴な実装、Keras)で重みの更新結果を比較します。使用するデータセットは手計算とあまり変わりませんが次の点が大きく異なります。
中間層を2段にして3層のネットワークにします。
活性化関数は多値分類を想定したものに設定します。
重みの初期値は乱数で設定します。
エポックを5に設定して処理系の差を顕在化させます。
重みの更新が終わったところで次の2パターンについて全ての重みを比較します。
Fiber vs. 素朴な実装(行列による実装)
Fiber vs. Keras(著名なフレームワーク)
#--------------------------------------------------
# 現実的な更新(Fiber)
#--------------------------------------------------
def real_Fiber(w, x_train, t_train, epochs, eta):
core = CoreFiber
model = Model(3, eta, linear) # 入力層(入力数 = 3)
model.add(3, sigmoid, sigmoid_der) # 中間層(ニューロン数 = 3)
model.add(3, sigmoid, sigmoid_der) # 中間層(ニューロン数 = 3)
model.add(3, softmax) # 出力層(ニューロン数 = 3)
model.measurer(cat_xentropy, cat_accuracy) # 測定系の関数(損失関数、評価関数)を設定
core.coreinit(model, w)
model.fit(x_train, t_train, epochs=epochs, batch_size=1, verbose=0)
return core.coredump(model)
#--------------------------------------------------
# 現実的な更新(素朴な実装―3層)
#--------------------------------------------------
def real_Plain_3Layer(w, x_train, t_train, epochs, eta):
w_mi1 = w[0].copy().T # 重みを初期化
w_mi2 = w[1].copy().T
w_out = w[2].copy().T
for epoch in range(epochs):
y_mi1 = sigmoid(x_train @ w_mi1) # 順伝播
y_mi2 = sigmoid(y_mi1 @ w_mi2)
y_out = softmax(y_mi2 @ w_out)
dlt_out = y_out - t_train # 逆伝播
dlt_mi2 = (dlt_out @ w_out.T) * sigmoid_der(y_mi1 @ w_mi2)
dlt_mi1 = (dlt_mi2 @ w_mi2.T) * sigmoid_der(x_train @ w_mi1)
w_out -= eta * np.outer(y_mi2, dlt_out) # 重みを更新
w_mi2 -= eta * np.outer(y_mi1, dlt_mi2)
w_mi1 -= eta * np.outer(x_train, dlt_mi1)
return [w_mi1.T, w_mi2.T, w_out.T]
#--------------------------------------------------
# 現実的な更新(Keras)
#--------------------------------------------------
def real_Keras(w, x_train, t_train, epochs, eta):
core = CoreKeras
model = keras.Sequential([ # 入力層(入力数 = 3)
keras.layers.Dense( # 中間層(ニューロン数 = 3)
3, 'sigmoid', False, input_shape=(3,)),
keras.layers.Dense( # 中間層(ニューロン数 = 3)
3, 'sigmoid', False),
keras.layers.Dense( # 出力層(ニューロン数 = 3)
3, 'softmax', False)
])
for i in range(len(w)):
w[i] = w[i].copy().T
core.coreinit(model, w)
sgd = keras.optimizers.SGD(
learning_rate=eta, momentum=0.0, nesterov=False
)
model.compile(
optimizer=sgd,
loss='categorical_crossentropy',
metrics=['accuracy']
)
model.fit(x_train, t_train, epochs=epochs, batch_size=1, verbose=0)
return [core.T for core in core.coredump(model)]
#--------------------------------------------------
# 動作確認(現実的な更新)
#--------------------------------------------------
w0 = glorot_uniform(3, 3) # 中間層1の重みの初期値
w1 = glorot_uniform(3, 3) # 中間層2の重みの初期値
w2 = glorot_uniform(3, 3) # 出力層の重みの初期値
ini_w = [w0, w1, w2]
x_train = np.array([ [0.1, 0.5, 0.9] ]) # 特徴量データ
t_train = np.array([ [0, 1, 0] ]) # 正解値データ
limit = 1e-7 # 許容できる差分の限界
eta = 0.1 # 学習率
epochs = 5 # エポック
nnm_w = real_Fiber(ini_w, x_train, t_train, epochs, eta)
pln_w = real_Plain_3Layer(ini_w, x_train, t_train, epochs, eta)
ktf_w = real_Keras(ini_w, x_train, t_train, epochs, eta)
print('Fiberが算出した重み')
show_coredump(nnm_w)
print('\n素朴な実装が算出した重み')
show_coredump(pln_w)
print('\nKerasが算出した重み')
show_coredump(ktf_w)
print('\n重みの差分(Fiber vs. 素朴な実装)')
show_corediff(nnm_w, pln_w, limit)
print('\n重みの差分(Fiber vs. Keras)')
show_corediff(nnm_w, ktf_w, limit)

結果の重みの差分を見るとFiberとKerasでは微妙に結果が異なることが分かります。しかし、FiberとKerasでは計算方法が異なることや重みの差分が十分に許容範囲内$${(10^{-7})}$$にあることから問題無しとしました。
演習編
演習の主要な目的は今回実装したニューラルネットワーク「Fiber」が期待通りに動作することを確信したいことにあります。そのためデータ分析やチューニングの視点はなく、もっぱらデータを投入して動作確認を行っています。演習の題目は次の4つです。
【演習1】二値分類―論理回路を再現する
【演習2】二値分類―タイタニック号の生存者を予測する
【演習3】多値分類―アヤメの特徴から品種を推測する
【演習4】多値分類―手書きの数字を認識する
データセットと前処理
演習の題目から想像がついたかも知れませんが、演習では機械学習で良く知られているデータセットを使用します。これは演習で疑問が生じたときに先達の演習を調べることによって疑問の解決を図ろうという目論見です。機械学習では3種類のデータセット(トレーニングセット、バリデーションセット、テストセット)を使いますが、Fiberの演習ではハイパーパラメータを探索しないのでバリデーションセットは使いません。演習で使うデータセットを図にしておきます。

生のデータセットはニューラルネットワークに投入できる形式に変換する必要があります。この変換を行うための前処理の典型的な手順は次のようになります。(前処理には欠損データの処理やラベルエンコーディングなども含まれますが記述を簡潔にするため省略しました。)
データセットの中から次の2種類のカラムを選定します。
特徴量として使用するカラム
正解値として使用するカラム
特徴量データを作成するには、スケーラを使って特徴量カラムのデータを標準化(または正規化)します。
正解値データを作成するには、エンコーダを使って正解値カラムのデータをOne-Hot化します。
これでニューラルネットワークに投入できる形式のデータセットを用意できましたが、演習で使用するにはあと少しの処理が必要です。
データセットをシャッフルします。
データセットをトレーニングセットとテストセットに分割します。
トレーニングセットはモデルを最適化するために使います。テストセットは最適化の終わった学習済みモデルの精度を確認するためにを使います。
こうして出来上がった4種類のデータは最低限のものですがFiberの演習には充分です。図では4種類のデータに変数名を付記してあります。これは演習のコードでも実際に使っている名前なので理解の助けになります。
演習の流れ
演習はおおよそ次のような流れに沿って進めていきます。この過程はコードで一気に実行されます。
モデルを効率よく最適化できるようにするため、データセットの前処理を行います。
レイヤ、ニューロン、活性化関数などの構成を決めてモデルを組み立てます。
モデルにトレーニングセットを投入して最適化を行います。
モデルにテストセットを投入して性能を評価します。
モデルにテストセットを投入して予測(再現、推測、認識)を行います。
最後にまとめて学習曲線、性能、予測結果、特徴量データを表示します。
演習で表示される内容のスクリーンショットを載せておきますが、最適化には乱数を使うのでGoogle Colabでの実行結果がこのスクリーンショットと同じになることはありません。
演習で使用するデータセットを取得
データセットはGoogle DriveやGoogle Colabの環境設定を必要としないものを選定しました。データセットは2箇所から取得します。「タイタニック号の乗客」はSeabornから、そして「アヤメの特徴」と「手書きの数字」はscikit-learnからです。「手書きの数字」にはMNISTというもっと有名なものがありますが、演習レベルでは似たような結果が出ることと環境設定の手間を考えてscikit-learnに収録されている方を残すことにしました。
titanic = sns.load_dataset('titanic') # タイタニック号の乗客
iris = load_iris() # アヤメの特徴
digits = load_digits() # 手書きの数字演習をサポートするユーティリティ
次の8つのユーティリティが演習をサポートします。
shuffle_and_split ― シャッフル&データセットを分割
preproc_seaborn ― データセットを前処理(seabornデータセット/二値分類)
preproc_scikit ― データセットを前処理(scikit-learnデータセット/多値分類)
show_progress ― 最適化の経過を表示
show_perform ― モデルの性能を表示
show_summary_logic ― テスト結果の要約を表示(二値分類/論理回路専用)
show_summary_bin ― テスト結果の要約を表示(二値分類)
show_summary_cat ― テスト結果の要約を表示(多値分類)
#--------------------------------------------------
# シャッフル&データセットを分割
#--------------------------------------------------
def shuffle_and_split(xo, to, x, t, ratio):
def shuffle(xo, to, x, t): # 要素の対応関係を保ったままシャッフル
pack = list(zip(xo, to, x, t))
np.random.shuffle(pack)
return zip(*pack)
def split(xo, to, x, t, ratio): # データセットをトレーニングセットとテストセットに分割
offset = int(len(x) * ratio)
ds = Object()
ds.x_train = np.array(x[:offset]) # トレーニングセット
ds.t_train = np.array(t[:offset])
ds.x_test = np.array(x[offset:]) # テストセット
ds.t_test = np.array(t[offset:])
ds.x_test_org = np.array(xo[offset:]) # テストセット(原本;テストで使用)
ds.t_test_org = np.array(to[offset:])
return ds
(xo, to, x, t) = shuffle(xo, to, x, t)
return split(xo, to, x, t, ratio)
#--------------------------------------------------
# データセットを前処理(seabornデータセット/二値分類)
#--------------------------------------------------
def preproc_seaborn(dset, x_colm, t_colm, c_colm, ratio):
def catenc(cpy, c_colm): # カテゴリを数値化
cpy = org.copy() # ラベルエンコードで破壊的操作を行うのでコピーを使う
enc = prep.LabelEncoder() # カテゴリの数値化にラベルエンコーダを使用する
for cat in c_colm:
cpy[cat] = enc.fit_transform(cpy[cat]) # カラムをエンコード結果に入れ替える(破壊的操作)
return cpy
xandt = x_colm + t_colm # データセット = 特徴量データ+正解値データ
org = dset[xandt].dropna(how='any') # 最適化で使うカラムを選択/欠損値が存在する行を削除
cpy = catenc(org.copy(), c_colm) # カテゴリを数値化
scaler = prep.StandardScaler() # スケーラを標準化に設定
x = scaler.fit_transform(cpy[x_colm]) # 特徴量カラムに標準化を実行
t = cpy[t_colm].values # 正解値カラムを選択
xo = org[x_colm].values
to = org[t_colm].values
return shuffle_and_split(xo, to, x, t, ratio) # シャッフル&データセットを分割
#--------------------------------------------------
# データセットを前処理(scikit-learnデータセット/多値分類)
#--------------------------------------------------
def preproc_scikit(dset, ratio):
scaler = prep.StandardScaler() # スケーラを標準化に設定
x = scaler.fit_transform(dset.data) # 標準化を実行
enc = prep.OneHotEncoder(sparse_output=False)
t = dset.target.reshape(-1, 1)
t = enc.fit_transform(t) # 正解値カラムをOne-Hot化
xo = dset.data
to = dset.target
return shuffle_and_split(xo, to, x, t, ratio) # シャッフル&データセットを分割
#--------------------------------------------------
# 最適化の経過を表示
#--------------------------------------------------
def show_progress(fit):
plt.ylim(0.0, 1.2)
plt.grid()
plt.plot(fit.loss, label='loss')
plt.plot(fit.accu, label='accuracy')
plt.xlabel('epochs')
plt.legend()
plt.show()
print('\n最適化の最終結果:')
print(f' 損失 = {fit.loss[-1]:.8f}')
print(f' 精度 = {fit.accu[-1]:.8f}')
#--------------------------------------------------
# モデルの性能を表示
#--------------------------------------------------
def show_perform(bef, aft):
print('\nモデルの性能(最適化の前→後):')
print(f' 損失 = {bef.loss:.8f} → {aft.loss:.8f}')
print(f' 精度 = {bef.accu:.8f} → {aft.accu:.8f}')
#--------------------------------------------------
# テスト結果の要約を表示(二値分類/論理回路専用)
#--------------------------------------------------
def show_summary_logic(logic, x, y, t):
print('\nテスト結果の要約:')
for (x, y, t) in zip(x, y, t):
pred = np.round(y).astype('int')
targ = np.round(t)
rslt = judge(pred == targ)
print(f' {logic}: 入力値 = {x.tolist()}, ', end='')
print(f'予測値 = [{y[0]:.8f}] ⇨ {pred}, 正解値 = {targ}, {rslt}')
#--------------------------------------------------
# テスト結果の要約を表示(二値分類)
#--------------------------------------------------
def show_summary_bin(y, t):
print('\nテスト結果の要約:')
for (y, t) in zip(y, t):
ystr = ', '.join([f'{f:.8f}' for f in y])
pred = np.round(y).astype('int')
targ = np.round(t)
rslt = judge(pred == targ)
print(f' 予測値 = [{ystr}] ⇨ {pred}, 正解値 = {targ}, {rslt}')
#--------------------------------------------------
# テスト結果の要約を表示(多値分類)
#--------------------------------------------------
def show_summary_cat(y, t, pholder):
print('\nテスト結果の要約:')
for (y, t) in zip(y, t):
ystr = ', '.join([f'{f:.{pholder}f}' for f in y])
pred = np.argmax(y)
targ = np.argmax(t)
rslt = judge(pred == targ)
print(f' 予測値 = [{ystr}] ⇨ {pred}, 正解値 = {targ}, {rslt}')【演習1】二値分類―論理回路を再現する
演習1では論理回路のAND, OR, XORを再現します。ANDとORは中間層が無くても(出力層にニューロンを1個配置するだけでも)再現できますが、これだとXORは絶対に再現できない(線形分離できない)ところが面白いです。演習では中間層を追加してXORを再現しています。
x_train = np.array([ # 特徴量データ
[0, 0], [0, 1], [1, 0], [1, 1]
])
target = { # 正解値データ
'AND': np.array([ 0, 0, 0, 1 ]),
'OR': np.array([ 0, 1, 1, 1 ]),
'XOR': np.array([ 0, 1, 1, 0 ])
}
logic = 'XOR' # 再現する論理回路を設定
t_train = target[logic] # 正解値データを確定
model = Model(2, eta=0.1) # 入力層(入力数 = 2)
model.add(20, relu, relu_der, fini=he_normal) # 中間層(ニューロン数 = 20)
model.add(1, sigmoid, fini=xavier_normal) # 出力層(ニューロン数 = 1)
model.measurer(bin_xentropy, bin_accuracy) # 測定系の関数(損失関数、評価関数)を設定
bef = model.evaluate(x_train, t_train) # 最適化「前」の性能を取得
fit = model.fit(x_train, t_train, epochs=100, batch_size=1, verbose=0) # 最適化
aft = model.evaluate(x_train, t_train) # 最適化「後」の性能を取得
y_train = model.predict(x_train) # 特徴量データ4件に対する予測値を取得
show_progress(fit) # 最適化の経過を表示
show_perform(bef, aft) # モデルの性能を表示
show_summary_logic(logic, x_train, y_train, t_train) # テスト結果の要約を表示


【演習2】二値分類―タイタニック号の生存者を予測する
演習2ではタイタニック号の乗客リスト(席等級、性別、年齢など)から生存者を予測します。この演習ではFiberによる最適化であまり精度が出なかったのでKerasでも実行してみました。結果は両者で似たような傾向だったので深追いせずに受け入れることにしました。
▣ Fiber
x_colm = ['pclass', 'sex', 'age', 'sibsp', 'parch', 'fare', 'embarked']
t_colm = ['survived'] # 正解値データ
c_colm = ['sex', 'embarked']
ds = preproc_seaborn(titanic, x_colm, t_colm, c_colm, 0.75) # 標準化を実行
lim = 10 # 予測で使うテストセットを10件に制限
model = Model(len(x_colm), eta=0.01) # 入力層(入力数 = x_colmの要素数)
model.add(10, relu, relu_der, fini=he_normal) # 中間層(ニューロン数 = 10)
model.add(1, sigmoid, fini=xavier_normal) # 出力層(ニューロン数 = 1)
model.measurer(bin_xentropy, bin_accuracy) # 測定系の関数(損失関数、評価関数)を設定
bef = model.evaluate(ds.x_test, ds.t_test) # 最適化「前」の性能を取得
fit = model.fit(ds.x_train, ds.t_train, epochs=50, batch_size=1, verbose=0) # 最適化
aft = model.evaluate(ds.x_test, ds.t_test) # 最適化「後」の性能を取得
y_test = model.predict(ds.x_test[:lim]) # テストセット10件に対する予測値を取得
show_progress(fit) # 最適化の経過を表示
show_perform(bef, aft) # モデルの性能を表示
show_summary_bin(y_test, ds.t_test) # テスト結果の要約を表示
raw = pd.DataFrame(ds.x_test_org[:lim], columns=x_colm)
raw['正解値(生存)'] = ds.t_test_org[:lim]
std = pd.DataFrame(ds.x_test[:lim], columns=x_colm)
print('\n実際に投入された特徴量データ(未処理)(10件):')
display(raw)
print('\n実際に投入された特徴量データ(処理済)(10件):')
display(std)




▣ Keras
bef = Object()
fit = Object()
aft = Object()
model = keras.Sequential([ # 入力層(入力数 = 7)
keras.layers.Dense( # 中間層(ニューロン数 = 10)
10, 'relu', kernel_initializer='he_normal', input_shape=(7,)),
keras.layers.Dense( # 出力層(ニューロン数 = 1)
1, 'sigmoid', kernel_initializer='lecun_normal')
])
sgd = keras.optimizers.SGD(learning_rate=0.01)
model.compile(optimizer=sgd, loss='binary_crossentropy', metrics=['accuracy'])
(bef.loss, bef.accu) = model.evaluate(ds.x_test, ds.t_test) # 最適化「前」の性能を取得
history = model.fit(ds.x_train, ds.t_train, epochs=50, batch_size=1, verbose=0)
(aft.loss, aft.accu) = model.evaluate(ds.x_test, ds.t_test) # 最適化「後」の性能を取得
y_test = model.predict(ds.x_test[:lim]) # テストセット10件に対する予測値を取得
fit.loss = history.history['loss']
fit.accu = history.history['accuracy']
show_progress(fit) # 最適化の経過を表示
show_perform(bef, aft) # モデルの性能を表示
show_summary_bin(y_test, ds.t_test) # テスト結果の要約を表示


【演習3】多値分類―アヤメの特徴から品種を推測する
演習3ではアヤメの特徴(花弁と萼片のサイズ)から品種(setosa, versicolor, virginica)を推測します。よくありそうな学習曲線を描いているのでニューラルネットワークにとっては得意な題目だと思います。
ds = preproc_scikit(iris, 0.75) # 標準化を実行
lim = 10 # 予測で使うテストセットを10件に制限
model = Model(4, eta=0.01) # 入力層(入力数 = 4) 4つの特徴
model.add(32, sigmoid, sigmoid_der) # 中間層(ニューロン数 = 32)
model.add(3, softmax) # 出力層(ニューロン数 = 3) 3品種に分類
model.measurer(cat_xentropy, cat_accuracy) # 測定系の関数(損失関数、評価関数)を設定
bef = model.evaluate(ds.x_test, ds.t_test) # 最適化「前」の性能を取得
fit = model.fit(ds.x_train, ds.t_train, epochs=50, batch_size=1) # 最適化
aft = model.evaluate(ds.x_test, ds.t_test) # 最適化「後」の性能を取得
y_test = model.predict(ds.x_test[:lim]) # テストセット10件に対する予測値を取得
show_progress(fit) # 最適化の経過を表示
show_perform(bef, aft) # モデルの性能を表示
show_summary_cat(y_test, ds.t_test[:lim], 8) # テスト結果の要約を表示
raw = pd.DataFrame(ds.x_test_org[:lim], columns=iris.feature_names)
raw['正解値(品種)'] = ds.t_test_org[:lim]
std = pd.DataFrame(ds.x_test[:lim], columns=iris.feature_names)
print('\n実際に投入された特徴量データ(未処理)(10件):')
display(raw)
print('\n実際に投入された特徴量データ(処理済)(10件):')
display(std)

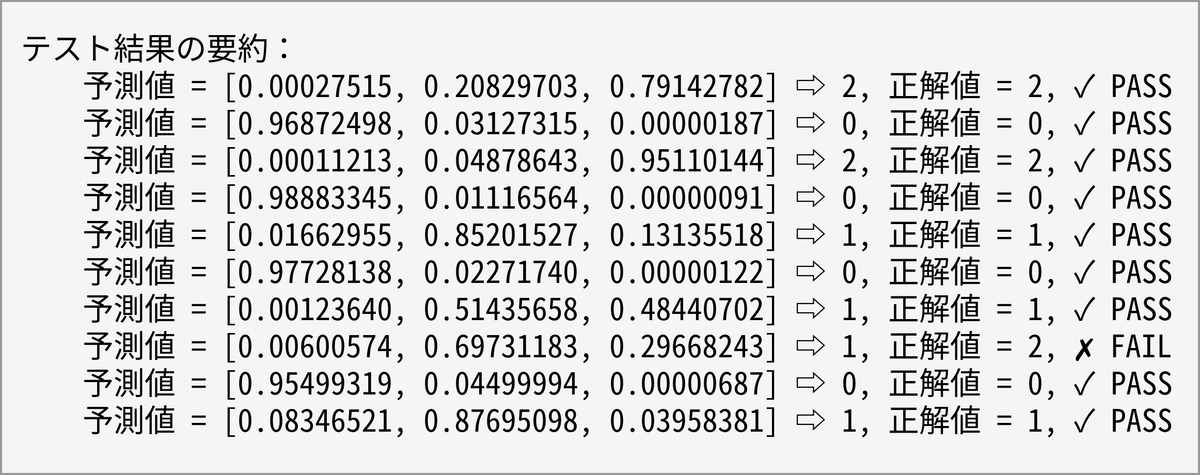


【演習4】多値分類―手書きの数字を認識する
演習4では手書きの数字を認識します。Fiberは素のニューラルネットワークなので畳み込みニューラルネットワーク(CNN)と比べると画像認識は不得意だろうと予想すると思いますが、手書きの数字程度なら望外に高い精度で認識します。
digits.data = digits.data[:500]
digits.target = digits.target[:500]
ds = preproc_scikit(digits, 0.75) # 標準化を実行
lim = 10 # 予測で使うテストセットを10件に制限
model = Model(64, eta=0.01) # 入力層(入力数 = 64) 8x8画素
model.add(30, sigmoid, sigmoid_der) # 中間層(ニューロン数 = 30)
model.add(10, softmax) # 出力層(ニューロン数 = 10) 0-9を識別
model.measurer(cat_xentropy, cat_accuracy) # 測定系の関数(損失関数、評価関数)を設定
bef = model.evaluate(ds.x_test, ds.t_test) # 最適化「前」の性能を取得
fit = model.fit(ds.x_train, ds.t_train, epochs=50, batch_size=50) # 最適化
aft = model.evaluate(ds.x_test, ds.t_test) # 最適化「後」の性能を取得
y_test = model.predict(ds.x_test[:lim]) # テストセット10件に対する予測値を取得
show_progress(fit) # 最適化の経過を表示
show_perform(bef, aft) # モデルの性能を表示
show_summary_cat(y_test, ds.t_test, 2) # テスト結果の要約を表示
ds.x_test_org = ds.x_test_org[:lim].astype(int).reshape(lim, 8, 8)
print('\n実際に投入された特徴量データ(正解値と画像)(10件/8x8画素):')
plt.figure(figsize=(6, 4))
plt.subplots_adjust(wspace=0, hspace=0)
for (i, (img, t)) in enumerate(zip(ds.x_test_org, ds.t_test)):
plt.subplot(2, 5, i + 1)
plt.axis('off')
plt.title(np.argmax(t))
plt.imshow(img, cmap='Greys') # 手書きの数字の階調情報を画像化
plt.show()
raw = pd.DataFrame(ds.x_test_org[0])
std = pd.DataFrame(np.round(ds.x_test[0].reshape(8, 8), 4))
print('\n実際に投入された特徴量データ(未処理)(1件/8x8画素):')
display(raw)
print('\n実際に投入された特徴量データ(処理済)(1件/8x8画素):')
display(std)


実際に投入された特徴量データ(正解値と画像)(10件/8x8画素):



おわりに
タイトルを「ニューラルネットワークの仕組みが知りたい」としましたが依然として分からないことが多いです。原因の1つは手っ取り早く実装を済ませて、後からゆっくりと数式と向き合えば良いと考えたことです(動くものを観察しないとモチベーションが上がらないタチなので)。次の段階に進むとすれば、手始めに合成関数と連鎖律をしっかりと押さえ込むところから始めるのでしょうか。
実装においてはニューロンを使いたいがために行列による演算を採用しませんでした。今となっては物足りなさを感じていますが、データフローダイアグラム(DFD)をほど良く再現できているのでこれはこれで良かったのだと思います。
ここから先は数式と向き合うのも良いし、当初は全く考えていなかった行列を使った実装も有り得る気がしてきました。そうではなくて、思いっ切り方向転換してフレームワーク(scikit-learn, Keras, TensorFlow, PyTorch, etc.)を使って実践的な問題を楽しむのも良いと思います。どこに向かって進むにしても、先に進むための足掛かりを得た気がします(そもそもの勘違い)。
更新履歴
2023-07-19、初版
2023-07-21、図解編に「連鎖律を使って式を立てる」を追加
この記事が気に入ったらサポートをしてみませんか?
