研究室が決まった！

私は現在大学三年生であり、ついに配属される研究室が決定した。その専門分野とは"離散数学"である。

離散数学って何？

離散数学（りさんすうがく、英: discrete mathematics）とは、原則として離散的な（言い換えると連続でない、とびとびの）対象を扱う数学のことである。有限数学または離散数理と呼ばれることもある。(wikipediaより抜粋)

こう言われても結局どういうことなの？という人が多いと思うため離散数学の中でも大きな分野である「組み合わせ論」と「グラフ理論」の二つについてそれぞれ話していこうと思う。

組み合わせ論

大きな分野の一つである組み合わせ論とはすなわち「数え上げの数学」である。例えて言うならばn人の人を並べる組み合わせはいくつあるか、nチームあるリーグの試合はいくつあるかなどがあげられる。

しかし一つの学問を形作っているものであるためこの例のように簡単なわけではない。実際に以下のような頭の痛くなるような式も出てくる。(これはある集合の和集合について一般化した式である。)

包除原理

この式もそうであるがやはり組み合わせ論は(今回は集合を)数え上げているのである。

グラフ理論

もう一つのグラフ理論は所謂"グラフ"ではなく以下のように点と線で作られるつながりのことである。

グラフ

私は特にこの分野が好きである。というのもこの世界は実はグラフにあふれている。思いつきやすい例で言えば駅と線路、ほかにも人間と交友関係などもグラフであると考えることができる。
ここでグラフ理論を用いた面白いトピックを二つ紹介しようと思う。

ケーニヒスベルクの橋

まず一つがケーニヒスベルクの橋である。これは以下のような七つの橋を一回ずつわたることはできるかという問題である。

ケーニヒスベルクの橋

この問題は何と以下のようなグラフを一筆書きできるかという問題に置き換えることができるのである。

ケーニヒスベルクの橋のグラフ

結論を言えばこれは一筆書きできない。
これはかの天才数学者オイラーが証明したことで知られている。

四色定理

これは四色あればどのような地図でも隣り合う国同士で色を被せずに塗り切ることができるという定理である。
疑いたくなるものであると思われるため実際に手元に適当な地図を書いて塗ってみてほしい。塗り切れてしまうはずである。

四色定理

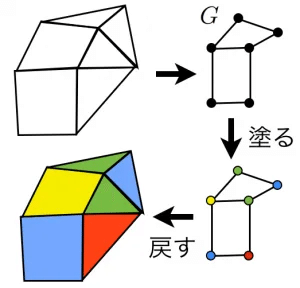
この問題も上のようにグラフで表すことができる。
しかし実はこの問題は理論的に証明されてはおらず1000時間以上コンピュータに計算させるという力業によって証明されてしまった。そのため今でも未解決であると主張する勢力がいるとかいないとか。
このようにグラフは意外なところで使うことができ大変面白い。

なぜ離散数学を選んだか

実は私はこの分野が第一志望ではない。というのも私の学部はどちらかというとデータサイエンスや統計学など実際の社会に根差した学問が主流であり私もそちらを目指していたのである。しかし成績が振るわず志望の低い純粋数学の研究室に行きついたというわけである。
しかし選んだ道を正解にするのは私の信条であり将来の応用のための基礎固めとして精進していきたいと考えるようにしたのである。

最後に

私は文理選択をする前から理系として生きてきたため研究室での研究は学問としてのこれまでの集大成である。学部の一年に加え大学院の二年間、ひと時も無駄にしないように励んでいきたいと思う。